既然，我們已經證明，保持 AVL 樹的平衡將會使性能得到很大的提升，那我們看看如何在程序中向樹插入一個新的鍵值。因為所有的新鍵是作為葉節點插入樹的，而新葉子的平衡因子為零，所以我們對新插入的節點不作調整。不過一旦有新葉子的插入我們必須更新其父節點的平衡因子。新葉子會如何影響父節點的平衡因子取決于葉節點是左子節點還是右子節點。如果新節點是右子節點，父節點的平衡因子減 1。如果新節點是左子節點，父節點的平衡因子將加 1。這種關系可以遞歸地應用于新節點的前兩個節點，并有可能影響到之前的每一個甚至是根節點。由于這是一個遞歸的過程，我們看看更新平衡因子的兩個基本條件：

• 遞歸調用已到達樹的根。
• 父節點的平衡因子已調整為零。一旦子樹平衡因子為零，那么父節點的平衡因子不會發生改變。

我們將實現 AVL 樹的子類BinarySearchTree。首先，我們將重寫_put方法，并寫一個新的輔助方法updateBalance。這些方法如Listing 1 所示。除了第 7 行和第 13 行對 updateBalance的調用，你會注意到_put和簡單的二叉搜索樹的定義完全相同。

Listing 1

def _put(self,key,val,currentNode): 
    if key < currentNode.key: 
        if currentNode.hasLeftChild(): 
                self._put(key,val,currentNode.leftChild) 
        else: 
                currentNode.leftChild = TreeNode(key,val,parent=currentNode) 
                self.updateBalance(currentNode.leftChild) 
    else: 
        if currentNode.hasRightChild(): 
                self._put(key,val,currentNode.rightChild) 
        else: 
                currentNode.rightChild = TreeNode(key,val,parent=currentNode) 
                self.updateBalance(currentNode.rightChild) 
 
def updateBalance(self,node): 
    if node.balanceFactor > 1 or node.balanceFactor < -1: 
        self.rebalance(node) 
        return 
    if node.parent != None: 
        if node.isLeftChild(): 
                node.parent.balanceFactor += 1 
        elif node.isRightChild(): 
                node.parent.balanceFactor -= 1 
 
        if node.parent.balanceFactor != 0: 
                self.updateBalance(node.parent) 

 updateBalance方法完成了大部分功能，實現了我們剛提到的遞歸過程。這個再平衡方法首先檢查當前節點是否完全不平衡，以至于需要重新平衡(第 16 行)。如果當前節點需要再平衡，那么只需要對當前節點進行再平衡，而不需要進一步更新父節點。如果當前節點不需要再平衡，那么父節點的平衡因子就需要調整。如果父節點的平衡因子不為零， 算法通過父節點遞歸調用updateBalance方法繼續遞歸到樹的根。

當對一棵樹進行再平衡是必要的，我們該怎么做呢?高效的再平衡是使 AVL 樹能夠很好地執行而不犧牲性能的關鍵。為了讓 AVL 樹恢復平衡，我們會在樹上執行一個或多個“旋轉”(rotation)。

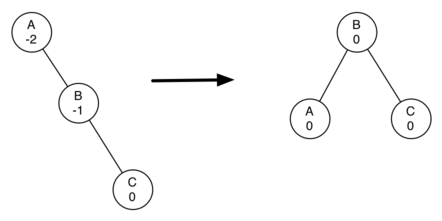
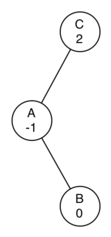
為了了解什么是旋轉，讓我們看一個很簡單的例子。思考一下圖 3 的左邊的樹。這棵樹是不平衡的，平衡因子為 -2。為了讓這棵樹平衡我們將根的子樹節點 A 進行左旋轉。

 圖 3：使用左旋轉變換不平衡樹

執行左旋轉我們需要做到以下幾點：

• 使右節點(B)成為子樹的根。
• 移動舊的根節點(A)到新根的左節點。
• 如果新根(B)原來有左節點，那么讓原來B的左節點成為新根左節點(A)的右節點。

注：由于新根(B)是 A 的右節點，在這種情況下，移動后的 A 的右節點一定是空的。我們不用多想就可以給移動后的 A 直接添加右節點。

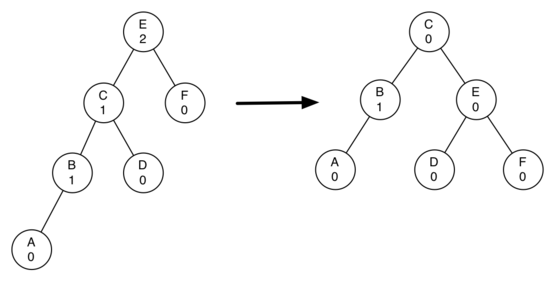
雖然這個過程概念上看起來簡單，但實現時的細節有點棘手，因為要保持二叉搜索樹的所有性質，必須以絕對正確的順序把節點移來移去。此外，我們需要確保更新了所有的父節點。讓我們看一個稍微復雜的樹來說明右旋轉。圖 4 的左側展現了一棵“左重”的樹，根的平衡因子為 2。執行一個正確的右旋轉，我們需要做到以下幾點：

• 使左節點(C)成為子樹的根。
• 移動舊根(E)到新根的右節點。
• 如果新根(C)原來有右節點(D)，那么讓 D 成為新根右節點(E)的左節點。

注：由于新根(C)是 E 的左節點，移動后的 E 的左節點一定為空。這時可以直接給移動后的 E 添加左節點。

 圖 4：使用右旋轉變換不平衡樹

現在你已經明白了旋轉的過程，了解了旋轉的方法，讓我們看看代碼。Listing 2 同時顯示了右旋轉和左旋轉的代碼。在第 2 行，我們創建一個臨時變量來跟蹤新的子樹的根。正如我們之前所說的新的根是舊根的右節點。現在，右節點已經存儲在這個臨時變量中。我們將舊根的右節點替換為新根的左節點。

下一步是調整兩個節點的父指針。如果newRoot原來有左節點，左節點的新父節點變成舊根。新根的父節點將成為舊根的父節點。如果舊根是整個樹的根，那么我們必須讓整棵樹的根指向這個新的根。如果舊根是左節點，那么我們改變左節點的父節點到一個新的根;否則，我們改變右節點的父節點到一個新的根(第 10-13 行)。最后我們設置的舊根的父節點成為新的根。這里有很多復雜的中間過程，所以建議你一邊看函數的代碼，一邊看圖 3。rotateRight方法和rotateLeft是對稱的，所以請自行研究rotateRight的代碼。

Listing 2

def rotateLeft(self,rotRoot): 
    newRoot = rotRoot.rightChild 
    rotRoot.rightChild = newRoot.leftChild 
    if newRoot.leftChild != None: 
        newRoot.leftChild.parent = rotRoot 
    newRoot.parent = rotRoot.parent 
    if rotRoot.isRoot(): 
        self.root = newRoot 
    else: 
        if rotRoot.isLeftChild(): 
                rotRoot.parent.leftChild = newRoot 
        else: 
            rotRoot.parent.rightChild = newRoot 
    newRoot.leftChild = rotRoot 
    rotRoot.parent = newRoot 
    rotRoot.balanceFactor = rotRoot.balanceFactor + 1 - min(newRoot.balanceFactor, 0) 
    newRoot.balanceFactor = newRoot.balanceFactor + 1 + max(rotRoot.balanceFactor, 0) 

 最后，第 16-17 行需要解釋一下。這兩行我們更新了舊根和新根的平衡因子。因為其他操作都是移動整個子樹，被移動的子樹內的節點的平衡因子不受旋轉的影響。但我們如何在沒有重新計算新的子樹的高度的情況下更新平衡因子?下面的推導將讓你明白，這些代碼都是正確的。

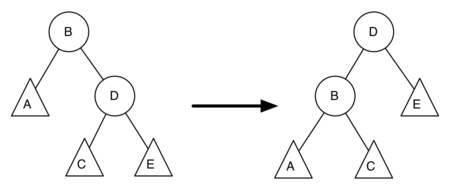
 圖 5：左旋轉

圖5顯示了一個左旋轉。B 和 D 是中心節點，A，C，E 是其子樹。讓 hX 表示以X為根節點的子樹的高度。通過定義我們知道：

newBal(B)=hA−hC

oldBal(B)=hA−hD

但我們知道，D 的高度也可以通過 1 + max(hC,hE) 給定，也就是說，D 的高度為兩子樹高度中較大者加 1。記住，hC 和 hE 沒有改變。所以，把上式代入第二個方程，可以得到：

oldBal(B)=hA−(1+max(hC,hE))

然后兩方程作差。下面是作差的步驟，newBal(B) 使用了一些代數方法簡化方程。

beginsplitnewBal(B)−oldBal(B)=hA−hC−(hA−(1+max(hC,hE)))

newBal(B)−oldBal(B)=hA−hC−hA+(1+max(hC,hE))

newBal(B)−oldBal(B)=hA−hA+1+max(hC,hE)−hC

newBal(B)−oldBal(B)=1+max(hC,hE)−hC

接下來我們移動 oldBal(B) 到方程的右端并利用 max(a,b)−c = max(a−c,b−c)。

newBal(B)=oldBal(B)+1+max(hC−hC,hE−hC)

但 hE − hC 等同于 −oldBal(D)。所以我們說：max(−a,−b) = −min(a,b)，可以通過以下步驟完成對 newBal(B) 的推導：

newBal(B)=oldBal(B)+1+max(0,−oldBal(D))

newBal(B)=oldBal(B)+1−min(0,oldBal(D))

現在方程所有的項都是已知數。如果我們記得 B 是rotRoot，D 是newRoot，可以看出這正好符合第 16 行的語句：

rotRoot.balanceFactor = rotRoot.balanceFactor + 1 - min(0,newRoot.balanceFactor) 

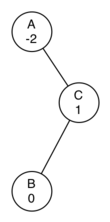
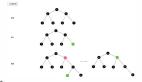
更新節點 D，以及右旋轉后的平衡因子的方程推導與此類似。現在你可能認為步驟都完全了解了。我們知道如何并且什么時候進行左右旋轉，但看看圖 6。由于節點 A 的平衡因子是 -2，我們應該做一個左旋轉。但是，當我們在左旋轉時會發生什么?

圖 6：一棵更難平衡的不平衡樹

 圖 7：顯示的樹左旋轉后，仍然不平衡。如果我們要做一個右旋轉來試圖再平衡，又回到了開始的狀態。

要解決這個問題，我們必須使用以下規則：

• 如果子樹需要左旋轉使之平衡，首先檢查右節點的平衡因子。如果右節點左重則右節點右旋轉，然后原節點左旋轉。
• 如果子樹需要右旋轉使之平衡，首先檢查左節點的平衡因子。如果左節點右重則左節點左旋轉，然后原節點右旋轉。

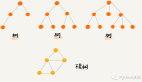
圖 8 顯示了這些規則如何解決了我們在圖 6 和圖 7 中遇到的問題。首先，以 C 為中心右旋轉，樹變成一個較好的形狀;然后，以 A 為中心左旋轉，整個子樹恢復平衡。

 圖 8：右旋轉后左旋轉

實現這些規則的代碼可以從我們“再平衡”(rebalance)的方法中找到，如Listing 3 所示。上面的第一條規則從第二行if語句中實現。第二條規則是由第 8 行elif語句實現。

Listing 3

def rebalance(self,node): 
  if node.balanceFactor < 0: 
         if node.rightChild.balanceFactor > 0: 
            self.rotateRight(node.rightChild) 
            self.rotateLeft(node) 
         else: 
            self.rotateLeft(node) 
  elif node.balanceFactor > 0: 
         if node.leftChild.balanceFactor < 0: 
            self.rotateLeft(node.leftChild) 
            self.rotateRight(node) 
         else: 
            self.rotateRight(node)  

通過保持樹的平衡，我們可以確保get方法運行的時間復雜度為 O(log2n)。但問題是put方法的時間復雜度是多少?我們把put操作進行分解。由于每一個新節點都是作為葉節點插入的，每一輪更新所有父節點的平衡因子最多只需要 log2n 次操作，每層執行一次。如果子樹是不平衡的最多需要兩個旋轉把子樹恢復平衡。但是，每個旋轉的操作的復雜度為 O(1) ，所以即使我們進行put操作最終的復雜度仍然是 O(log2n)。