通常在開(kāi)始學(xué)編程的時(shí)候，你會(huì)接觸一些常用數(shù)據(jù)結(jié)構(gòu)。

[[275700]]

到最后一般會(huì)學(xué)到哈希表。對(duì)于修讀計(jì)算機(jī)科學(xué)學(xué)位的朋友，你通常要上專門(mén)的數(shù)據(jù)結(jié)構(gòu)課，從了解有關(guān)鏈表、隊(duì)列和棧的各種知識(shí)。這些統(tǒng)稱為線性數(shù)據(jù)結(jié)構(gòu)，因?yàn)橐肋壿嫶涡驈念^排到尾。

當(dāng)你開(kāi)始進(jìn)入下一階段，學(xué)習(xí)樹(shù)和圖結(jié)構(gòu)時(shí)，事情就會(huì)顯得比處理線性數(shù)據(jù)結(jié)構(gòu)復(fù)雜很多。這促使我們專門(mén)寫(xiě)一篇文章來(lái)探討“樹(shù)”這種特定的數(shù)據(jù)結(jié)構(gòu)幫大家答疑解惑。

本文內(nèi)容包括:

• 樹(shù)的定義樹(shù)的結(jié)構(gòu)工作原理代碼實(shí)現(xiàn)

現(xiàn)在就開(kāi)始學(xué)習(xí)吧 :)

樹(shù)的定義

通常對(duì)編程新手來(lái)說(shuō)，線性數(shù)據(jù)結(jié)構(gòu)比樹(shù)和圖要更好理解。我們此處所說(shuō)的樹(shù)，即是以層次化方式組織和存放數(shù)據(jù)的特定數(shù)據(jù)結(jié)構(gòu)。

實(shí)例解析

為了理解“層次化”的意思，我們以家譜為例：里面有祖父母、父母、孩子、兄弟姐妹。這就是用層次化的模式來(lái)構(gòu)建家譜。

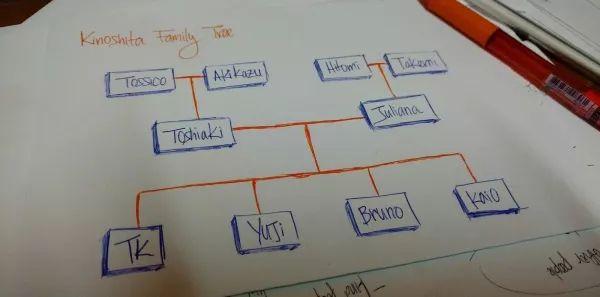
上圖就是我的家譜。Tossico，Akikazu，Hitomi和Takemi作為我的祖父母和外祖父母處于最頂層。Toshiaki 和 Juliana是我父母。TK，Yuji，Bruno 和 Kaio 則是我和我的的兄弟姐妹們。

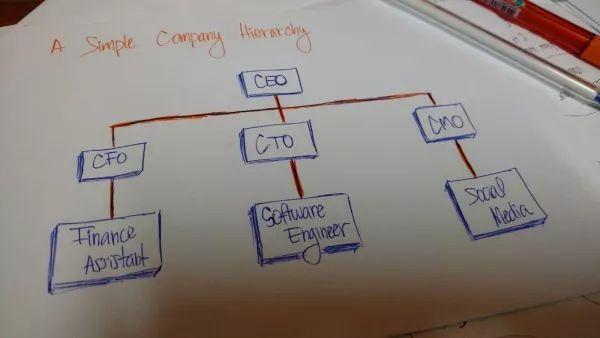
公司組織也是類似的層次化結(jié)構(gòu)

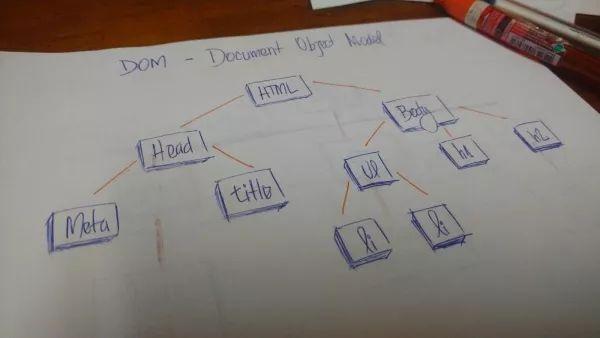
HTML的文檔模型對(duì)象 (DOM) 就是一棵樹(shù)最頂層 HTML 標(biāo)簽連接到 head 標(biāo)簽和 body 標(biāo)簽。二者又有對(duì)應(yīng)的子標(biāo)簽，比如 head 含有 meta 和 title 標(biāo)簽，body 含有與可視化內(nèi)容相關(guān)的 h1, a, li等標(biāo)簽。名詞定義

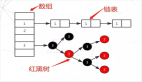
樹(shù)(tree)：是以邊(edge)相連的結(jié)點(diǎn)(node)的集合，每個(gè)結(jié)點(diǎn)存儲(chǔ)對(duì)應(yīng)的值(value/data)，當(dāng)存在子結(jié)點(diǎn)時(shí)與之相連。

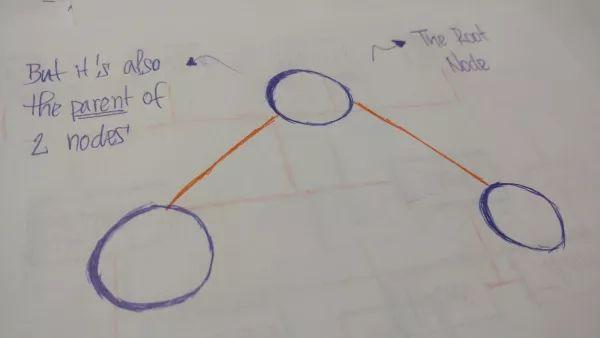
根結(jié)點(diǎn)(root)：是樹(shù)的首個(gè)結(jié)點(diǎn)，在相連兩結(jié)點(diǎn)中更接近根結(jié)點(diǎn)的成為父結(jié)點(diǎn)(parent node)，相應(yīng)的另一個(gè)結(jié)點(diǎn)稱為子結(jié)點(diǎn)(parent node)。

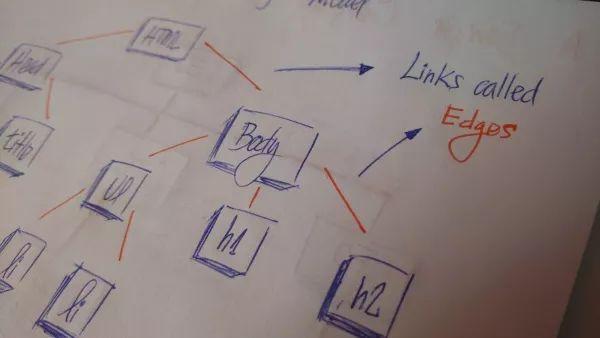
邊(edge)：所有結(jié)點(diǎn)都由邊相連，用于標(biāo)識(shí)結(jié)點(diǎn)間的關(guān)系。邊是樹(shù)中很重要的一個(gè)概念，因?yàn)槲覀冇盟鼇?lái)確定節(jié)點(diǎn)之間的關(guān)系。

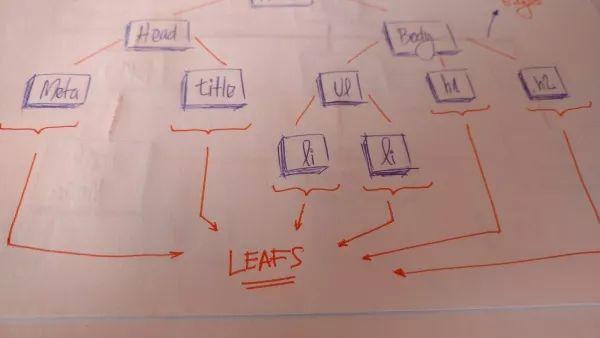
葉子結(jié)點(diǎn)(Leaves)：是樹(shù)的末端結(jié)點(diǎn)，他們沒(méi)有子結(jié)點(diǎn)，就像真實(shí)的樹(shù)那樣 ，由根開(kāi)始，伸展枝干，到葉為止。

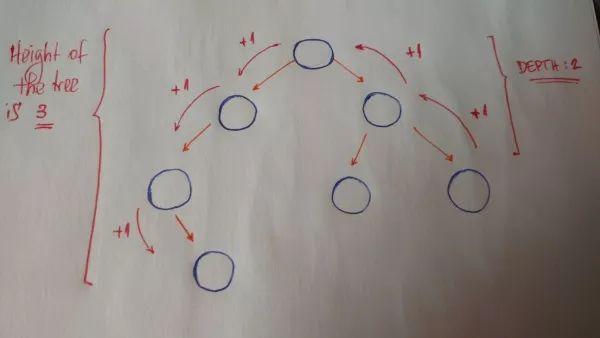
樹(shù)高(height)與結(jié)點(diǎn)深度(depth)也是很重要的概念。樹(shù)高：是由根結(jié)點(diǎn)出發(fā)，到子結(jié)點(diǎn)的最長(zhǎng)路徑長(zhǎng)度。結(jié)點(diǎn)深度：是指對(duì)應(yīng)結(jié)點(diǎn)到根結(jié)點(diǎn)路徑長(zhǎng)度。

二叉樹(shù)

現(xiàn)在來(lái)探討一種特殊的樹(shù)結(jié)構(gòu)-二叉樹(shù)(binary tree)，它每個(gè)節(jié)點(diǎn)最多有兩個(gè)子結(jié)點(diǎn)，亦稱左孩子和右孩子。

在計(jì)算機(jī)科學(xué)中，二叉樹(shù)是一種“樹(shù)”數(shù)據(jù)結(jié)構(gòu)，樹(shù)上的每個(gè)節(jié)點(diǎn)最多有兩個(gè)孩子，分別為左孩和右孩。——維基百科

來(lái)看一個(gè)二叉樹(shù)的實(shí)例。

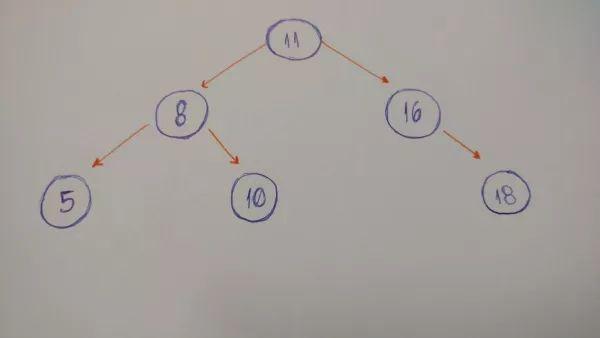
動(dòng)手寫(xiě)二叉樹(shù)

首先明確我們要實(shí)現(xiàn)的對(duì)象是一個(gè)結(jié)點(diǎn)集合，每個(gè)結(jié)點(diǎn)有三個(gè)屬性：值(value), 左孩子(left_child)和右孩子(right_child)。

寫(xiě)出來(lái)會(huì)是這個(gè)樣子：

我們寫(xiě)了一個(gè)BinaryTree類，在初始化實(shí)際對(duì)象的時(shí)候傳入對(duì)應(yīng)值，并在此時(shí)還沒(méi)有子結(jié)點(diǎn)的情況下將左右孩子設(shè)為空。

為什么要這么做呢?

因?yàn)楫?dāng)我們創(chuàng)建節(jié)點(diǎn)的時(shí)候，它還沒(méi)有孩子，我們只有節(jié)點(diǎn)數(shù)據(jù)。

讓我們測(cè)試一下：

下面到了插入結(jié)點(diǎn)的操作：在樹(shù)還沒(méi)有對(duì)應(yīng)子結(jié)點(diǎn)時(shí)新建結(jié)點(diǎn)，并賦值給現(xiàn)有結(jié)點(diǎn)對(duì)應(yīng)變量。否則，新建結(jié)點(diǎn)連接并替換掉現(xiàn)有位置子結(jié)點(diǎn)。

畫(huà)出來(lái)是這個(gè)樣子：

相應(yīng)代碼(左右相同)：

為了進(jìn)一步測(cè)試，讓我們構(gòu)建一個(gè)更復(fù)雜一些的樹(shù)：

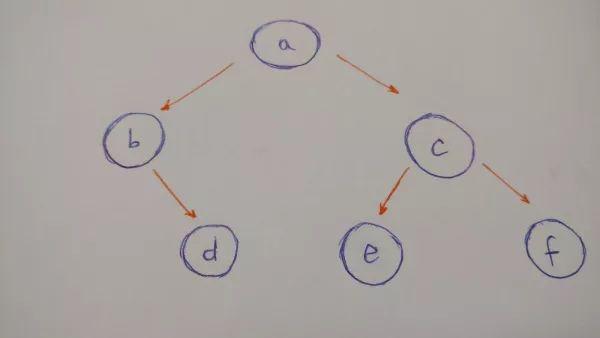
這棵樹(shù)共有六個(gè)結(jié)點(diǎn)，其中結(jié)點(diǎn)b沒(méi)有左孩子。對(duì)應(yīng)初始化并插入結(jié)點(diǎn)的代碼如下：

下一步讓我們看看如何對(duì)樹(shù)進(jìn)行遍歷。

一般來(lái)講我們有兩種遍歷方式：深度優(yōu)先遍歷(DFS)和 廣度優(yōu)先遍歷(BFS)，前者沿著特定路徑遍歷到根結(jié)點(diǎn)再轉(zhuǎn)換臨近路徑繼續(xù)遍歷，后者逐層遍歷整個(gè)樹(shù)結(jié)構(gòu)。來(lái)看具體的例子：

深度優(yōu)先遍歷 (DFS)

DFS會(huì)沿特定路徑遍歷到葉子結(jié)點(diǎn)再回溯 (backtracking)進(jìn)入臨近路徑繼續(xù)遍歷。以下面的樹(shù)結(jié)構(gòu)為例：

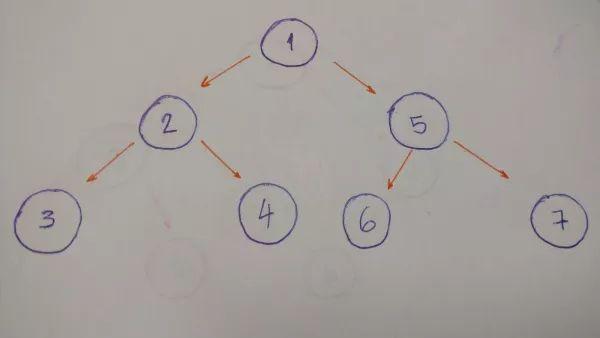
遍歷順序?yàn)?–2–3–4–5–6–7

具體來(lái)講，我們會(huì)先訪問(wèn)根結(jié)點(diǎn)1再訪問(wèn)其左孩子2，接著是2的左孩子3，到達(dá)葉子結(jié)點(diǎn)回溯一步，訪問(wèn)2的右孩子4，進(jìn)一步回溯，繼續(xù)順序訪問(wèn)5，6和7。在輸出遍歷結(jié)果時(shí)，據(jù)父結(jié)點(diǎn)值相對(duì)子結(jié)點(diǎn)輸出順序的不同，深度優(yōu)先遍歷又可細(xì)分為先序、中序和后序遍歷三種情況。

先序遍歷

即直接按照我們對(duì)結(jié)點(diǎn)的訪問(wèn)順序輸出遍歷結(jié)果即實(shí)現(xiàn)，父結(jié)點(diǎn)值被最先輸出。代碼：

中序遍歷

中序遍歷輸出結(jié)果為：3–2–4–1–6–5–7。

左孩子值最先輸出，然后是父結(jié)點(diǎn)，最后是右孩子。對(duì)應(yīng)代碼如下：

后序遍歷

后序遍歷輸出結(jié)果為：3–4–2–6–7–5–1.

左右孩子值依次輸出，最后是父結(jié)點(diǎn)，對(duì)應(yīng)代碼如下：

廣度優(yōu)先搜索 (BFS)

BFS：按照結(jié)點(diǎn)深度逐層遍歷樹(shù)結(jié)構(gòu)。

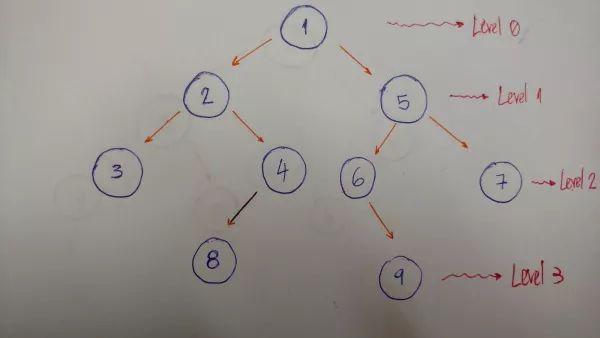
再拿上面的圖來(lái)實(shí)際解釋這種方法：

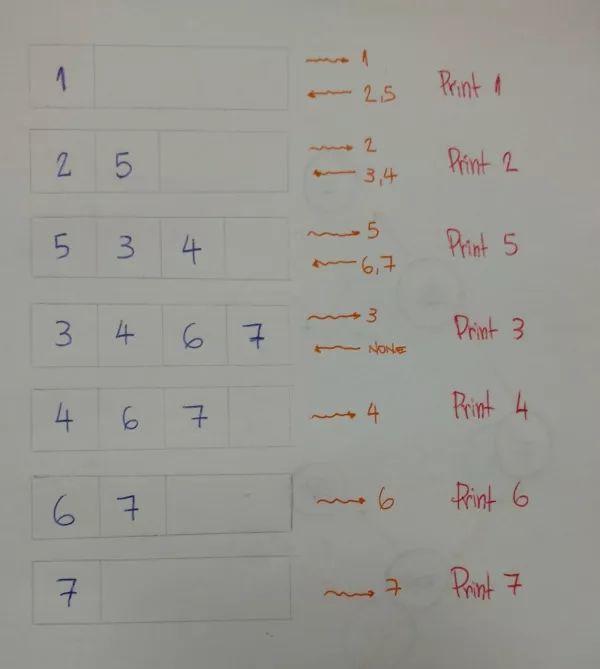
逐層每層從左到右進(jìn)行遍歷，對(duì)應(yīng)遍歷結(jié)果為：1–2–5–3–4–6–7。對(duì)應(yīng)代碼如下：

你應(yīng)該已經(jīng)注意到了，我們要借助先進(jìn)先出(FIFO)的隊(duì)列(queue)結(jié)構(gòu)完成操作，具體的出入隊(duì)列順序如下圖所示：

二叉搜索樹(shù)

二叉搜索樹(shù)又名有序二叉樹(shù)，結(jié)點(diǎn)元素按固定次序排布，使得我們可以在進(jìn)行查找等操作時(shí)使用二分搜索提高效率。——維基百科

它最明顯的特征是父結(jié)點(diǎn)值大于左子樹(shù)任意結(jié)點(diǎn)值，小于右子樹(shù)任意結(jié)點(diǎn)值。

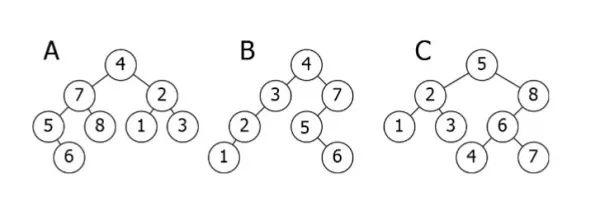
上圖以三個(gè)二叉樹(shù)為例，哪個(gè)才是正確的呢?

A 左右子樹(shù)需要進(jìn)行交換。B 滿足條件，是二叉搜索樹(shù)。C 值為4的結(jié)點(diǎn)需要移至3的右孩子處

接下來(lái)進(jìn)行二叉搜索插入、結(jié)點(diǎn)檢索、結(jié)點(diǎn)刪除以及平衡的解釋。

插入

假設(shè)以這種順序插入結(jié)點(diǎn): 50, 76, 21, 4, 32, 100, 64, 52。50會(huì)是我們初始的根結(jié)點(diǎn)。

再依次進(jìn)行如下操作：

76 大于50，置于右邊21 小于 50, 置于左邊4 置于21左邊

最終一氣呵成我們會(huì)得到下面這棵樹(shù)：

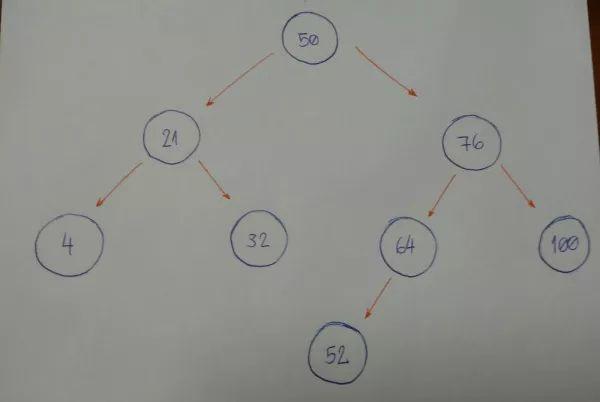
發(fā)現(xiàn)規(guī)律了么?像開(kāi)車一樣，從根結(jié)點(diǎn)駛?cè)耄迦胫荡笥诋?dāng)前結(jié)點(diǎn)值向右開(kāi)否則向左開(kāi)知道找到空位停車入庫(kù)。(嘀嘀嘀，老司機(jī))

代碼實(shí)現(xiàn)也很簡(jiǎn)單：

這個(gè)算法最牛逼的地方在于他的遞歸部分，你知道是哪幾行嗎?

結(jié)點(diǎn)檢索

其實(shí)結(jié)合我們的插入操作，檢索的方法就顯而易見(jiàn)，依舊從根結(jié)點(diǎn)開(kāi)始，小于對(duì)應(yīng)結(jié)點(diǎn)值左轉(zhuǎn)，大于右轉(zhuǎn)，等于報(bào)告找到，走到葉子結(jié)點(diǎn)都沒(méi)找到 gg，就報(bào)沒(méi)有該元素。例如我們想知道下圖中有沒(méi)有52這個(gè)值：

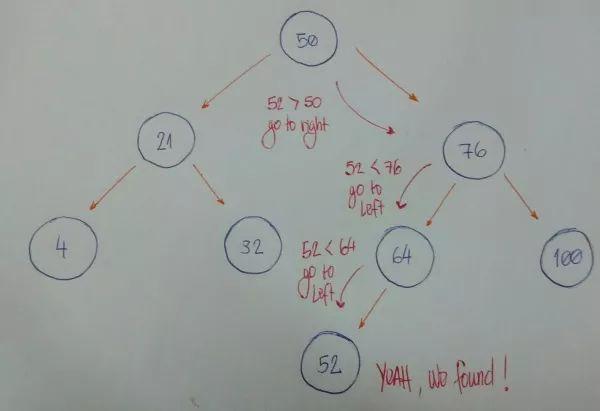
代碼如下：

刪除: 移除并重構(gòu)

刪除操作要更復(fù)雜一些，因?yàn)橐幚砣N不同情況：

情景 #1：葉子結(jié)點(diǎn)

是最簡(jiǎn)單的情況，直接刪除就好.

情景 #2：只有左孩子或右孩子

該情景等價(jià)于鏈表上的結(jié)點(diǎn)刪除，把當(dāng)前結(jié)點(diǎn)刪除并讓其子結(jié)點(diǎn)替換自己原來(lái)位置。

情景 #3：同時(shí)具有左右孩子的結(jié)點(diǎn)

找到該結(jié)點(diǎn)右子樹(shù)中最小值所在的結(jié)點(diǎn)，剔除要?jiǎng)h除的當(dāng)前結(jié)點(diǎn)并把最小值結(jié)點(diǎn)提升到空缺位置。

一些別的操作

清零：將三個(gè)屬性全部置None即可。

找到最小值：從根節(jié)點(diǎn)開(kāi)始，一直左轉(zhuǎn)，直到找不到任何結(jié)點(diǎn)為止，此時(shí)我們就找到了最小值。

恭喜你學(xué)完本篇內(nèi)容!數(shù)據(jù)結(jié)構(gòu)中的樹(shù)的內(nèi)容大致如此，趕緊收藏起來(lái)吧