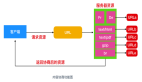
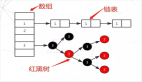
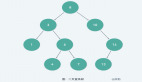
一文帶你速通 HashMap 底層核心數據結構紅黑樹
一、什么是紅黑樹
在權威書籍中,對于紅黑樹的解釋是這樣的:
- 每個節點或者紅色,或者是黑色。
- 根節點為黑色。
- 每一個葉子節點都是黑色。
- 如果一個節點是紅色,那么他的孩子節點都是黑色。
- 從任意一個節點,經過的黑色節點是一樣的。
在《算法4》一書中認為紅黑樹和2-3樹是等價的。

二、2-3樹詳解
2-3樹的2節點和3節點
很多人認為紅黑樹是2-3樹的另一種實現,所以在正式的介紹紅黑樹之前,我們不妨了解2-3樹,先來說說2-3樹的2節點,其性質如下:
- 滿足二分搜索樹的基本性質。(左節點小于節點,右節點大于節點)
- 節點分為2節點和3節點,2節點即可以掛兩個子節點。3節點即可掛3節點。
如下圖所示,這就是典型的2-3樹的2節點,可以看到2節點即父節點存放一個元素的節點,這種節點只能掛兩個元素。
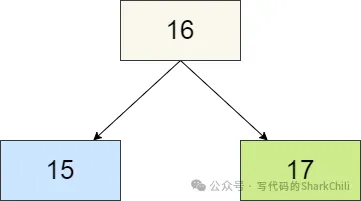
同理我們再給出3節點的圖例,可以看出3節點的就是由兩個節點拼接成的節點,其左中右分別可以掛一個子節點,由此我們才稱它為3節點。
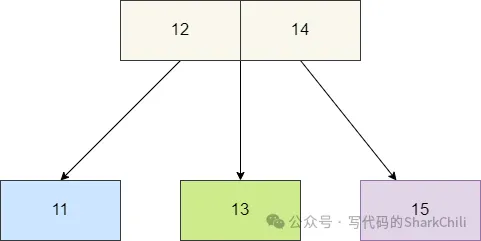
2-3樹是絕對平衡樹
絕對平衡樹的定義即任何時刻任意節點,左節點和右節點的層數都是一樣的。那么2-3樹是如何實現絕對平衡的呢?假設我們要將下面的節點存放到2-3樹中:
42 37 12 18 6 11 5首先添加42,由于2-3樹為空,所以直接插入即可。

再插入37 ,因為37比42小,所以理應插入到42的左節點中,但是左節點為空,所以它只能作為42的鄰節點,由此構成一個3節點。

再插入12,此時構成了一個4節點,不符合2-3樹節點的特征。

所以我們需要將4節點進程拆解,將37的左右鄰接節點全部拆為子節點:
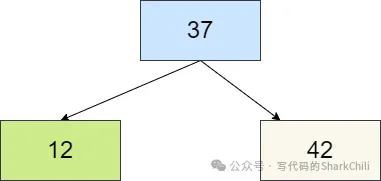
在添加18,比37小,比12大,所以要插入到12的右子節點,但是右子節點為空,所以18就和12合并變為3節點

再添加6構成一個4節點需要拆解,導致失衡:
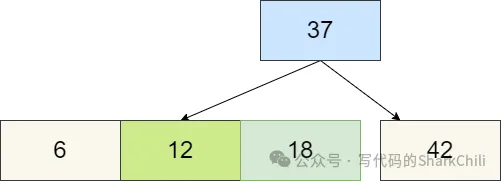
所以我們對這個4節點進程拆解,可以看到37的左右節點還是失衡。
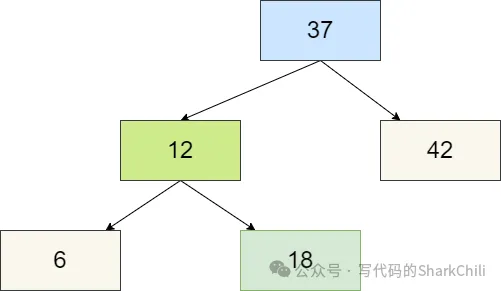
所以我們將12向上合并,和37構成3節點,最終2-3樹得以平衡。
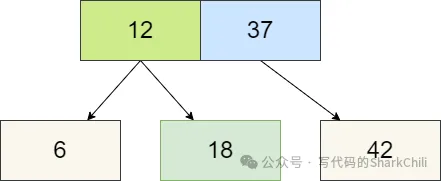
三、紅黑樹詳解
紅黑樹和2-3樹的關系
前文我們提到紅黑樹可以理解為2-3樹的另一種變體,我們以2-3樹的2節點為例,對應成紅黑樹的標識就是將2節點的左邊染紅并作為右節點的子節點,注意,筆者這里雖說12作為37的子節點,但是在紅黑樹的性質中,這兩個節點邏輯上可以理解為一個節點,這樣的理解便于我們后續了解紅黑樹的黑平衡。
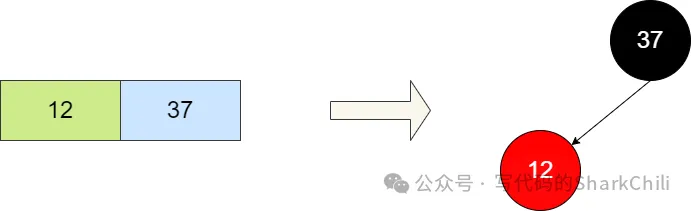
對應的,我們根據上面描述我們給出這樣一棵2-3樹,將其轉為紅黑樹:
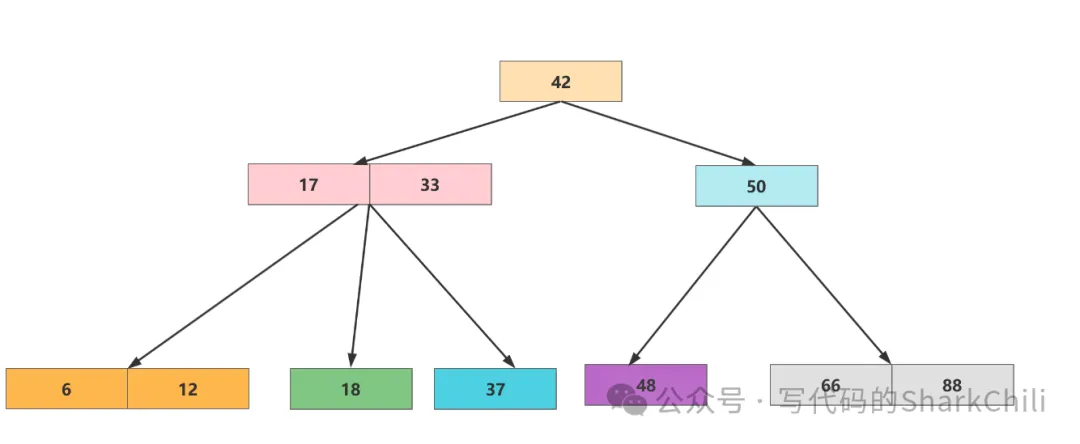
可以看到,轉為紅黑樹只需將2-3樹的3節點的左節點染紅,例如上圖的6、12組成的3節點,我們只需將6染紅,作為黑節點12的左節點即可。
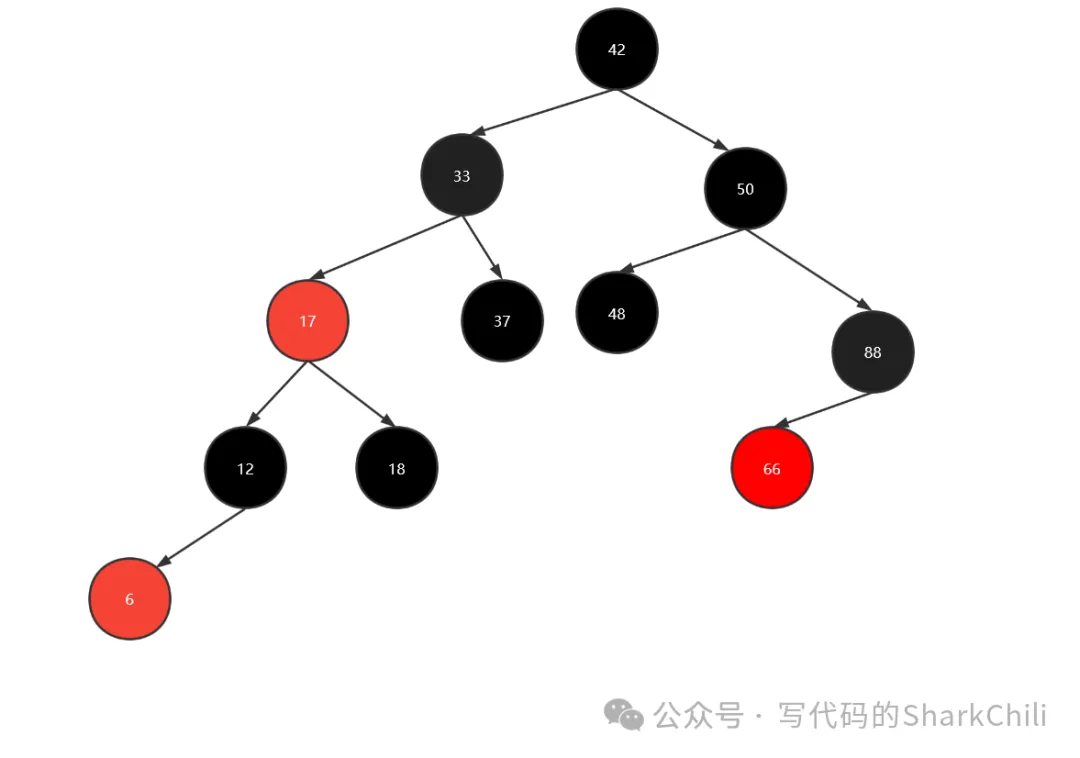
紅黑樹的性質詳解
了解了紅黑樹這個數據結構的圖例之后,我們來總結一下紅黑樹的特性:
從任意節點到另外一個葉子節點,經過的黑節點是一樣的。
嚴格意義上,紅黑樹是一個絕對的“黑平衡樹”,即我們將紅節點和其父節點當作一個整體,我們就會發現,這個紅黑樹的層級是絕對平衡的。而將"將紅節點和其父節(黑節點)點當作一個整體"的過程,就是2-3樹。
紅黑樹最大高度為2N(logN),所以添加復雜度估算為O(logN)
紅黑樹如何添加元素
(1) 添加一個比插入位置大的節點
以2-3數為例,假設我們樹中只有一個節點37,此時插入一個42,按照2-3樹的做法,會將42插入到37的右子節點,但此時2-3數還沒有右子節點,所以就將其添加到自己的右邊,構成3節點。

若是紅黑樹,42和37進行比對之后發現,42大于37,最終42就會以右子節點的姿態在37的右邊,很明顯這違背了紅黑樹的特征,所有的紅節點都必須位于左節點。所以我們需要對其進行左旋,并將右上節點染黑,左下節點染紅。
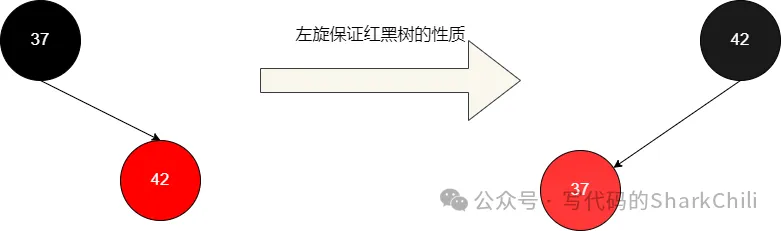
對于上述的左旋轉我們不妨來一個比較實際的例子,如下圖所示,假設經過一輪的插入之后37作為42的根節點,很明顯此時紅黑樹的狀態是失衡的(從黑平衡角度來看,37左邊有1層,42為2層,是失衡的)。

所以我們需要進行一次左旋轉,因為紅黑樹的性質保證黑節點37的右子樹都大于37,所以左旋時,先找到紅節點42的最小節點作為37的右子節點,于是37指向41:
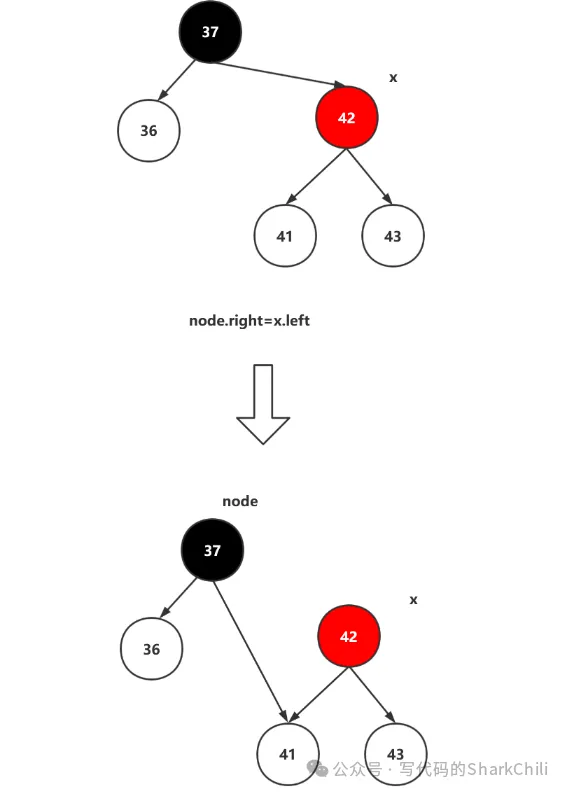
因為41頂替了紅節點42,42直接上升為父節點,自此以此保證黑平衡的左旋就完成了:
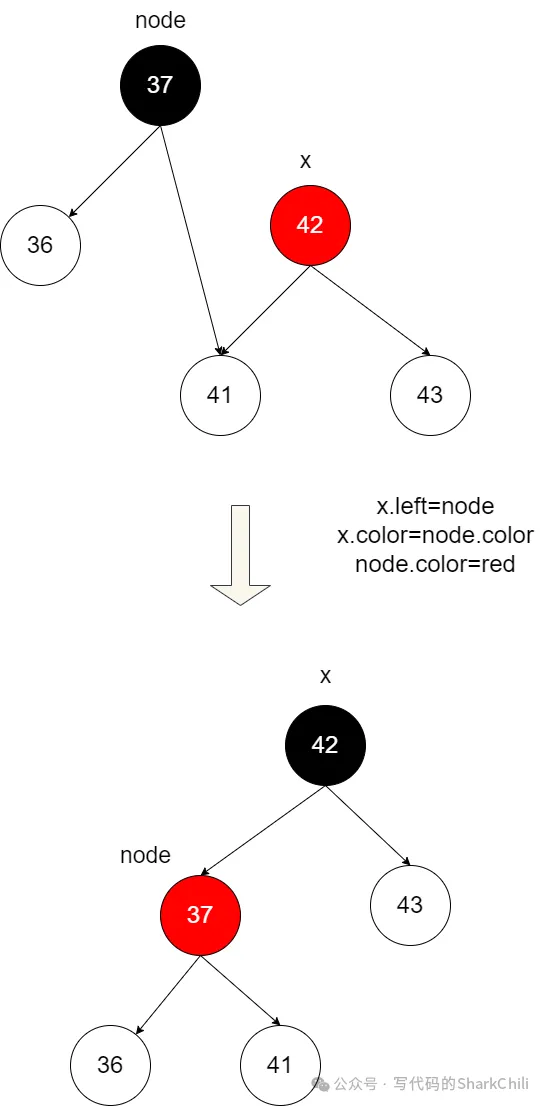
完整的代碼如下:
/**
* 插入的節點構成3節點,但是紅節點在左邊,需要進行左旋
*
* @param node
* @return
*/
private Node leftRotate(Node node) {
// 找到node節點的左節點
Node x = node.right;
//左旋
node.right = x.left;
x.left = node;
//顏色翻轉
x.color = node.color;
node.color = RED;
return x;
}(2) 連續添加兩個節點都在左邊
如下圖,構成了一個左傾斜的節點,導致失衡。
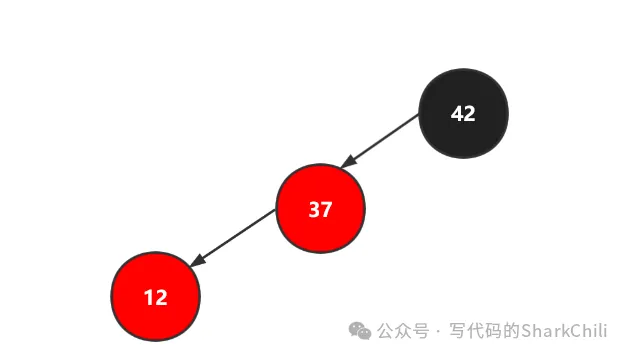
對此我們就需要進行一個右旋的操作,如下圖,因為紅黑樹的有序性,這使得42這個根節點大于左邊的所有節點,所以我們將左節點中最大的節點作為42的左節點,讓37作為根節點,完成黑平衡,如下圖。
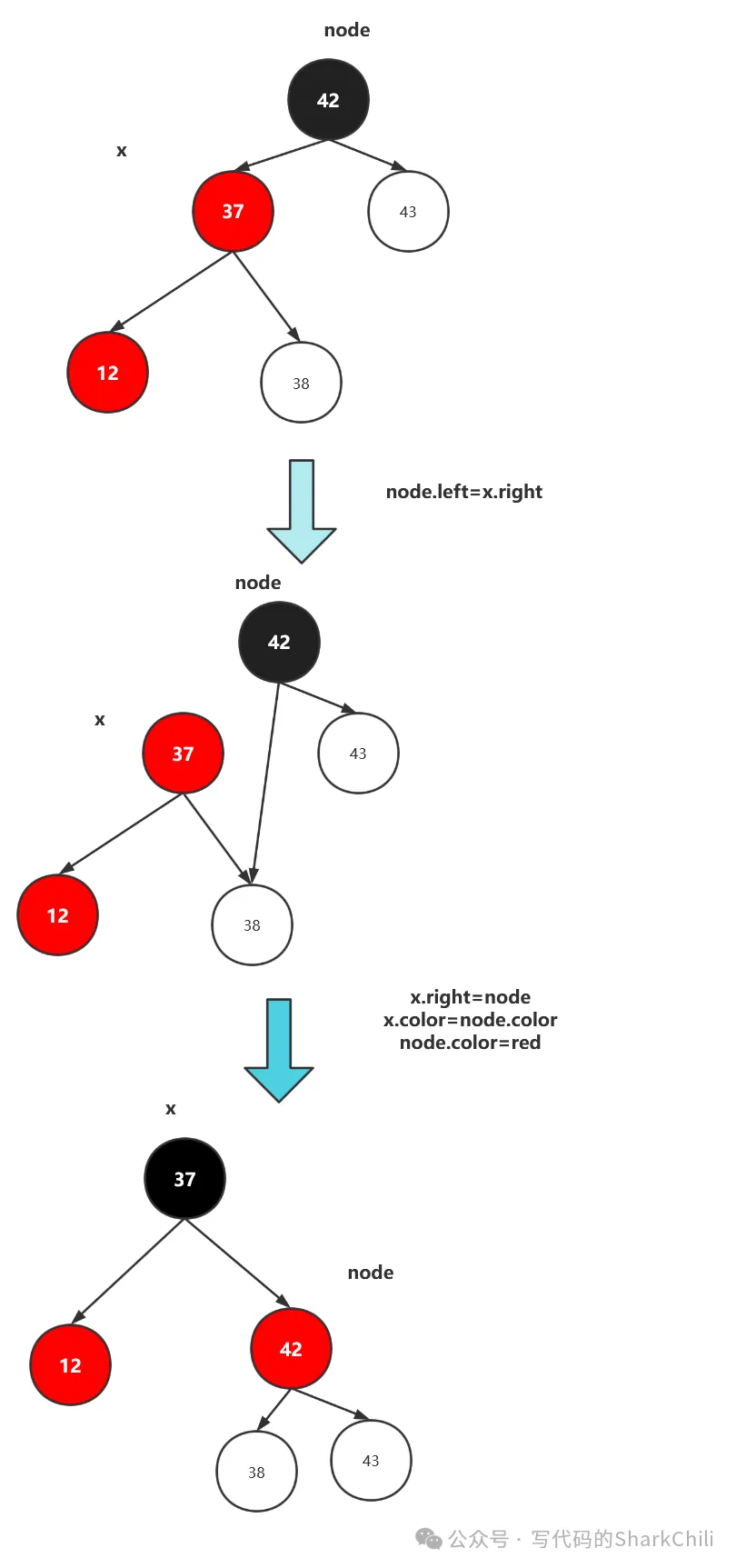
可以看到雖然完成了右旋轉的操作,但是最終的左右節點都是紅的,導致紅黑樹并不是黑平衡的,所以這里就需要一次顏色翻轉。這里我們先貼出右旋轉的代碼,在介紹顏色翻轉邏輯:
private Node rightRotate(Node node) {
Node x = node.left;
node.left = x.right;
x.right = node;
node.color = RED;
x.color = node.color;
return x;
}(3) 添加節點后子節點都變紅
在上文右旋操作導致,顏色錯誤進而出現紅黑樹違背黑平衡的情況,所以我們需要進行顏色翻轉,如下圖,我們將子節點都為紅的節點染黑,再將父節點染紅(父節點會將筆者后續的遞歸邏輯中變黑)。
這樣依賴37左節點層級為1,右節點層級也為1(黑平衡要求我們將左紅節點和黑節點看作一個整體)
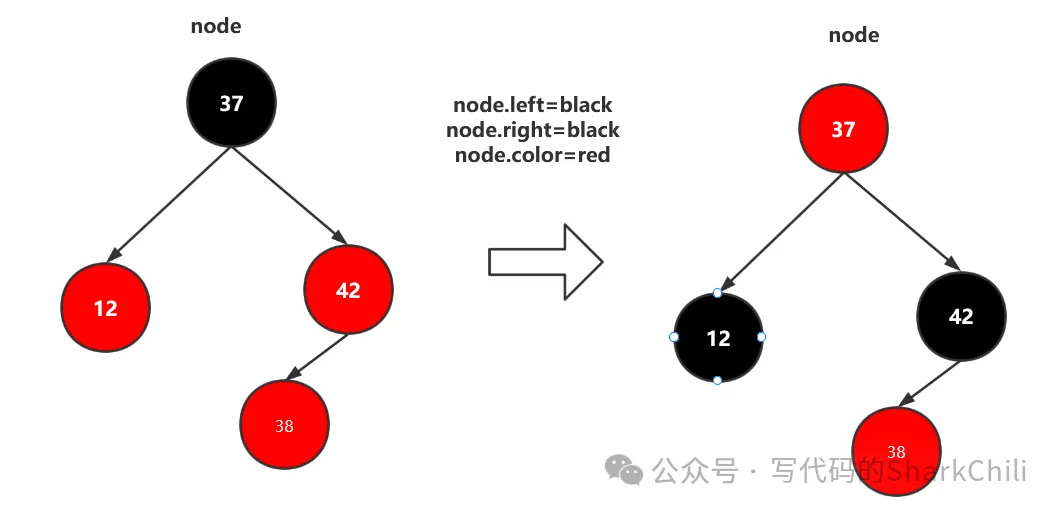
(4) 添加節點成為LR型
如下圖,LR型就是37 12 13這樣的插入順序,對此我們只需左旋再右旋最后顏色翻轉一下即可
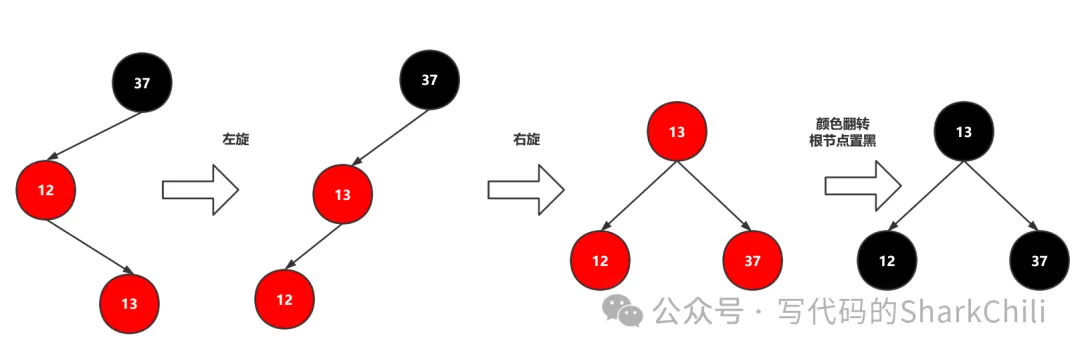
四、手寫一個紅黑樹
針對上述的圖解,我們給出實現紅黑樹的幾個問題點:
- 紅黑樹是由一個個節點構成,所以我們需要聲明節點內部類,內部類擁有顏色、左節點指針、右節點指針、key、value、顏色等幾個屬性。
- 有了節點內部類,我們就需要對紅黑樹類添加相關屬性描述了,首先是紅黑樹的容量、其次紅黑樹的操作都需要從樹根開始,所以我們需要首節點root、以及容量size。
- 紅黑樹插入都需要和每個key進行比較,所以紅黑樹類的k要求可以比較,所以我們定義的紅黑樹要求是泛型類,并且泛型key必須是可比較的,所以這個k泛型需要繼承Comparable。
完成這些鋪墊之后,我們就需要進行插入操作的邏輯分析了,我們不妨對上文長篇論述的插入過程進行整理一下:
- 插入的節點在當前節點右邊,導致紅節點在右邊,需要進行左旋轉保證黑平衡。
- 連續插入兩個節點都在當前節點左邊,導致向左傾斜,需要進行右旋轉保持平衡。
- 第一次插入的節點在當前節點左邊,然后再插入一個節點在紅黑樹右邊導致紅黑樹失衡。我們需要先左旋一下,再右旋一下。
- 當前節點的左節點和右節點都是紅色的,需要將顏色翻轉為黑色。
分析之后我們發現3這個一點包含了1、2的操作,所以我們編寫3、4兩個點的邏輯就可以實現上面的所有功能了,如下圖:
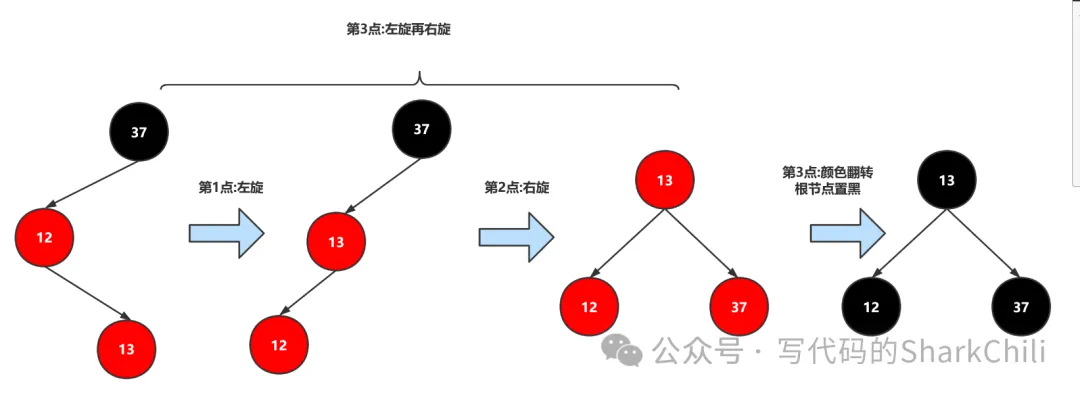
注意紅黑樹要求根節點為黑色,所以我們完成上述的操作之后,需要手動將根節點變為黑色。
對核心邏輯完成梳理之后,我們就可以開始對紅黑樹展開編碼了。首先我們需要創建紅黑樹類,可以看到我們聲明的k泛型繼承Comparable:
public class RedBlackTree<K extends Comparable<K>, V>對于節點顏色只有紅黑兩種,所以我們將其常量化:
private static final boolean RED = true;
private static final boolean BLACK = false;然后我們再根據上文的描述給出紅黑樹每個節點的成員變量:
private class Node<K, V> {
private K key;
private V val;
private Node left, right;
private boolean color;
public Node(K key, V val) {
this.key = key;
this.val = val;
this.left = null;
this.right = null;
this.color = RED;
}
}然后在進行紅黑樹容量、首節點、構造方法聲明:
private Node root;
private int size;
public RedBlackTree() {
this.root = null;
this.size = 0;
}終于我們可以正式實現節點添加邏輯,首選是左旋的邏輯,這一點我們在上文圖解添加過程時已經寫好了偽代碼,補充完成即可。
/**
* 插入的節點構成3節點,但是紅節點在左邊,需要進行左旋
*
* @param node
* @return
*/
private Node leftRotate(Node node) {
// 找到node節點的左節點
Node x = node.right;
//左旋
node.right = x.left;
x.left = node;
//顏色翻轉
x.color = node.color;
node.color = RED;
return x;
}右旋邏輯:
private Node rightRotate(Node node) {
Node x = node.left;
node.left = x.right;
x.right = node;
node.color = RED;
x.color = node.color;
return x;
}顏色翻轉:
private void flipColors(Node node) {
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}完成后我們就可以根據上文分析的添加邏輯,編寫3、4邏輯整合,首先為了代碼復用,我們編寫一下顏色判斷的邏輯,注意若節點不存在,我們也認定這個節點為黑:
private boolean isRed(Node<K, V> node) {
if (node == null) {
return false;
}
return node.color == RED;
}然后完成添加邏輯,可以看到筆者通過遞歸將3、4邏輯完成的紅黑樹的添加操作,完成添加操作并旋轉平衡后的當前節點。
private Node<K, V> add(Node<K, V> node, K key, V val) {
if (node == null) {
size++;
return new Node(key, val);
}
if (key.compareTo(node.key) < 0) {
node.left = add(node.left, key, val);
} else if (key.compareTo(node.key) > 0) {
node.right = add(node.right, key, val);
} else {
node.val = val;
}
// 左節點不為紅,右節點為紅,左旋
if (isRed(node.right) && !isRed(node.left)) {
node = leftRotate(node);
}
// 左鏈右旋
if (isRed(node.left) && isRed(node.left.left)) {
node = rightRotate(node);
}
// 顏色翻轉
if (isRed(node.left) && isRed(node.right)) {
flipColors(node);
}
return node;
}完成核心邏輯后,我們就將根節點變黑即可,考慮封裝性,我們將上文方法封裝成一個add允許外部傳鍵值進來。
public void add(K key, V val) {
root = add(root, key, val);
root.color = BLACK;
}補充剩余邏輯
獲取容量和獲取根節點:
public int getSize() {
return size;
}
private Node getRoot() {
return root;
}用層次遍歷法測試結果
我們希望測試紅黑樹添加的準確性,所以我們用嘗試用代碼添加以下幾個節點
150 172 194 271 293 370完成后的樹應該如下圖所示
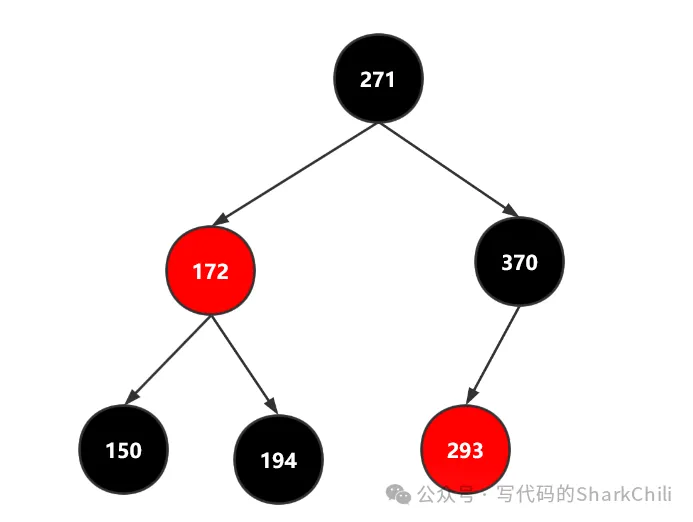
為了驗證筆者代碼的準確性,我們編寫一段層次遍歷的測試代碼,按層次順序以及顏色輸出節點
public void levelOrder() {
Node root = this.getRoot();
ArrayDeque<Node> queue = new ArrayDeque();
queue.add(root);
while (!queue.isEmpty()) {
Node node = queue.pop();
System.out.println("key:" + node.key + " val: " + node.val + " color:" + (node.color == RED ? "red" : "black"));
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}測試代碼,可以看到輸出結果正確
public static void main(String[] args) {
RedBlackTree<Integer, String> rbTree = new RedBlackTree<>();
rbTree.add(150, "");
rbTree.add(172, "");
rbTree.add(194, "");
rbTree.add(271, "");
rbTree.add(293, "");
rbTree.add(370, "");
rbTree.levelOrder();
/**
* 輸出結果
*
* key:271 val: color:black
* key:172 val: color:red
* key:370 val: color:black
* key:150 val: color:black
* key:194 val: color:black
* key:293 val: color:red
*/
}五、Java中HashMap關于紅黑樹的使用
插入
我們都知道Java中的HashMap在底層數組容量為64且當前這個bucket的鏈表長度達到8時會觸發擴容,對此我們不妨寫一段代碼測試一下,代碼如下所示,可以看到筆者為了更好的演示,將每一個map的value值聲明為當前key在hashMap底層數組中的索引位置。所以我們在map.put("590", "Idx:12");打上斷點
HashMap<String, String> map = new HashMap<String, String>(64);
map.put("24", "Idx:2");
map.put("46", "Idx:2");
map.put("68", "Idx:2");
map.put("29", "Idx:7");
map.put("150", "Idx:12");
map.put("172", "Idx:12");
map.put("194", "Idx:12");
map.put("271", "Idx:12");
map.put("293", "Idx:12");
map.put("370", "Idx:12");
map.put("392", "Idx:12");
map.put("491", "Idx:12");
//轉紅黑樹
map.put("590", "Idx:12");核心代碼如下所示,我們傳入的590的key會在i為12的鏈表中不斷查找空閑的位置,然后完成插入,循環過程中會記錄當前鏈表元素個數binCount ,經過判斷binCount >TREEIFY_THRESHOLD - 1即8-1=7,然后調用treeifyBin看看是擴容還是轉紅黑樹
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
//計算出hashMap這個key對應索引Ii的位置
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
....略
//核心邏輯在這里,我們傳入的590的key會在i為12的鏈表中不斷查找空閑的位置,然后完成插入,循環過程中會記錄當前鏈表元素個數binCount ,經過判斷binCount >TREEIFY_THRESHOLD - 1即8-1=7,然后調用treeifyBin轉紅黑樹
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1)
treeifyBin(tab, hash);
break;
}
.....
}
}
.........略
}我們再來看看treeifyBin,可以看到如果數組容量小于64直接擴容,反之就是將當前節點轉為樹節點然后調用treeify轉紅黑樹,關于紅黑樹的邏輯上文已經詳細說明了這里就不多贅述了。
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
//如果數組容量小于64直接擴容
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
do {
//將節點轉為樹節點,hd即為head指向當前鏈表頭節點,然后后續節點一次轉為樹節點和前驅節點彼此指向,從而構成一個雙向鏈表
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
//如果hd不為空說明需要轉紅黑樹,調用treeify
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}HashMap中的紅黑樹是如何完成查詢的呢?(重點)
HashMap源碼如下,首先通過hashCode找到桶的位置,然后判斷這個桶是否只有一個元素,如果沒有則直接返回,反之調用getTreeNode從紅黑樹中找到對應的元素
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
if ((tab = table) != null && (n = tab.length) > 0 &&
//計算hash對應的節點first
(first = tab[(n - 1) & hash]) != null) {
//如果有且只有一個則直接返回
if (first.hash == hash &&
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
//如果是紅黑樹則調用getTreeNode
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}我們步入getTreeNode會看到find方法,可以看到它查詢紅黑樹的元素邏輯很簡單,根據紅黑樹的有序性找到和查詢元素hash值相同、equals為true的節點返回即可。
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
TreeNode<K,V> p = this;
do {
int ph, dir; K pk;
TreeNode<K,V> pl = p.left, pr = p.right, q;
//比對元素hash值大于h,p指向p的左子節點進行下一次比對
if ((ph = p.hash) > h)
p = pl;
//比對值小于查詢節點的hash,p指向右子節點進行下一次比對
else if (ph < h)
p = pr;
//如果key一樣且equals為true直接返回這個元素
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if (pl == null)
p = pr;
else if (pr == null)
p = pl;
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr;
else if ((q = pr.find(h, k, kc)) != null)
return q;
else
p = pl;
} while (p != null);
return null;
}小結
本文通過圖解加實現為讀者演示了紅黑樹的特點和工作流程,可以看到紅黑樹的邏輯起始并沒有那么復雜,只要讀者專注核心概念,用一些簡單的示例畫圖了解過程,再通過需求分析所有邏輯和設計之后,編碼就沒有那么困難了。既使遇到問題,我們也可以抓住數據結構的特點,配合使用debug+中序遍歷也能解決邏輯漏洞。從而加深對數據結構的理解。
在此我們再對二分搜索樹、AVL樹、紅黑樹三者使用場景進行一下說明:
- 隨機添加節點:若節點存在大量隨機性,使用二分搜索樹即可,相比于紅黑樹的2O(nLogN)復雜度,二分搜索樹的O(logN)性能更佳,但是二分搜索樹可能存在退化成鏈表的情況,需謹慎考慮。
- 僅作查詢:對于查詢AVL最合適不過。他的平衡高度為logn比紅黑樹的“黑平衡”那種2logn的平衡要出色很多,在添加少,查詢多的情況下,使用AVL樹更合適。
- 綜合操作:若需要增刪改查等綜合操作,建議使用紅黑樹,紅黑樹雖然不是最優但是綜合上是最優的。