概述

梯度下降是神經網絡中流行的優化算法之一。一般來說，我們想要找到最小化誤差函數的權重和偏差。梯度下降算法迭代地更新參數，以使整體網絡的誤差最小化。

梯度下降是迭代法的一種,可以用于求解最小二乘問題(線性和非線性都可以)。在求解機器學習算法的模型參數，即無約束優化問題時，梯度下降(Gradient Descent)是最常采用的方法之一，另一種常用的方法是最小二乘法。在求解損失函數的最小值時，可以通過梯度下降法來一步步的迭代求解，得到最小化的損失函數和模型參數值。反過來，如果我們需要求解損失函數的最大值，這時就需要用梯度上升法來迭代了。在機器學習中，基于基本的梯度下降法發展了兩種梯度下降方法，分別為隨機梯度下降法和批量梯度下降法。

該算法在損失函數的梯度上迭代地更新權重參數，直至達到最小值。換句話說，我們沿著損失函數的斜坡方向下坡，直至到達山谷。基本思想大致如圖3.8所示。如果偏導數為負，則權重增加(圖的左側部分)，如果偏導數為正，則權重減小(圖中右半部分) 42 。學習速率參數決定了達到最小值所需步數的大小。

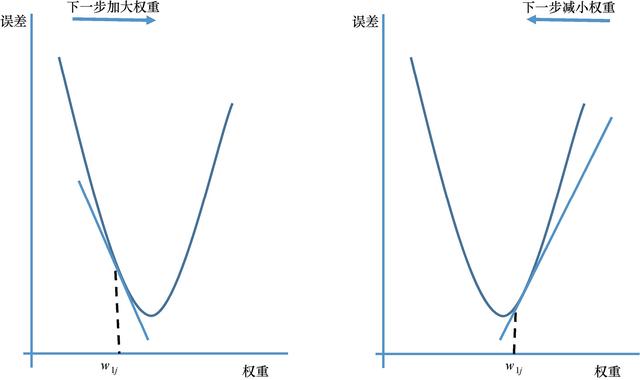
圖3.8　隨機梯度最小化的基本思想

誤差曲面

尋找全局最佳方案的同時避免局部極小值是一件很有挑戰的事情。這是因為誤差曲面有很多的峰和谷，如圖3.9所示。誤差曲面在一些方向上可能是高度彎曲的，但在其他方向是平坦的。這使得優化過程非常復雜。為了避免網絡陷入局部極小值的境地，通常要指定一個沖量(momentum)參數。

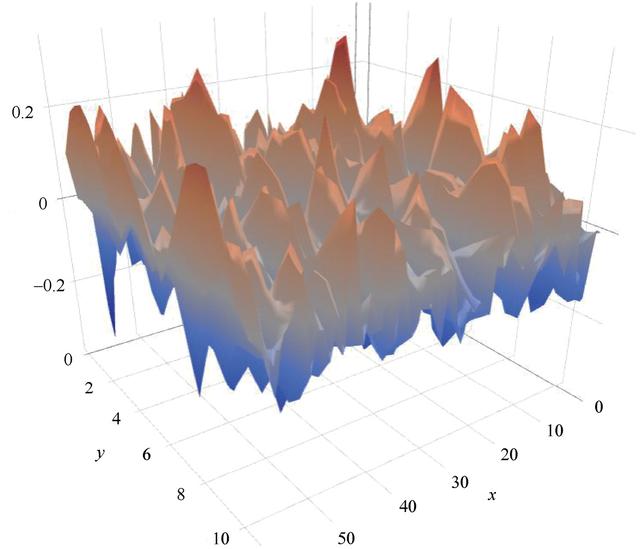
圖3.9　典型優化問題的復雜誤差曲面

我很早就發現，使用梯度下降的反向傳播通常收斂得非常緩慢，或者根本不收斂。在編寫第一個神經網絡時，我使用了反向傳播算法，該網絡包含一個很小的數據集。網絡用了3天多的時間才收斂到一個解決方案。幸虧我采取一些措施加快了處理過程。

說明 雖然反向傳播相關的學習速率相對較慢，但作為前饋算法，其在預測或者分類階段是相當快速的。

隨機梯度下降

傳統的梯度下降算法使用整個數據集來計算每次迭代的梯度。對于大型數據集，這會導致冗余計算，因為在每個參數更新之前，非常相似的樣本的梯度會被重新計算。隨機梯度下降(SGD)是真實梯度的近似值。在每次迭代中，它隨機選擇一個樣本來更新參數，并在該樣本的相關梯度上移動。因此，它遵循一條曲折的通往極小值的梯度路徑。在某種程度上，由于其缺乏冗余，它往往能比傳統梯度下降更快地收斂到解決方案。

說明 隨機梯度下降的一個非常好的理論特性是，如果損失函數是凸的 43 ，那么保證能找到全局最小值。

代碼實踐

理論已經足夠多了，接下來敲一敲實在的代碼吧。

一維問題

假設我們需要求解的目標函數是：

()=2+1f(x)=x2+1

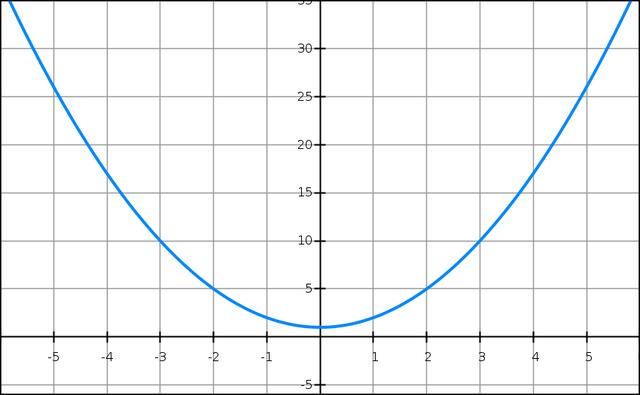
顯然一眼就知道它的最小值是 =0x=0 處，但是這里我們需要用梯度下降法的 Python 代碼來實現。

#!/usr/bin/env python 
# -*- coding: utf-8 -*- 
""" 
一維問題的梯度下降法示例 
""" 
 
 
def func_1d(x): 
 """ 
 目標函數 
 :param x: 自變量，標量 
 :return: 因變量，標量 
 """ 
 return x ** 2 + 1 
 
 
def grad_1d(x): 
 """ 
 目標函數的梯度 
 :param x: 自變量，標量 
 :return: 因變量，標量 
 """ 
 return x * 2 
 
 
def gradient_descent_1d(grad, cur_x=0.1, learning_rate=0.01, precision=0.0001, max_iters=10000): 
 """ 
 一維問題的梯度下降法 
 :param grad: 目標函數的梯度 
 :param cur_x: 當前 x 值，通過參數可以提供初始值 
 :param learning_rate: 學習率，也相當于設置的步長 
 :param precision: 設置收斂精度 
 :param max_iters: 最大迭代次數 
 :return: 局部最小值 x* 
 """ 
 for i in range(max_iters): 
 grad_cur = grad(cur_x) 
 if abs(grad_cur) < precision: 
 break # 當梯度趨近為 0 時，視為收斂 
 cur_x = cur_x - grad_cur * learning_rate 
 print("第", i, "次迭代：x 值為 ", cur_x) 
 
 print("局部最小值 x =", cur_x) 
 return cur_x 
 
 
if __name__ == '__main__': 
 gradient_descent_1d(grad_1d, cur_x=10, learning_rate=0.2, precision=0.000001, max_iters=10000) 

就是這么酷吧!用Python理解剃度下降!