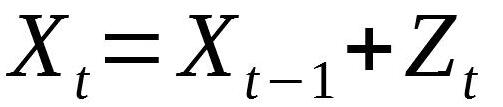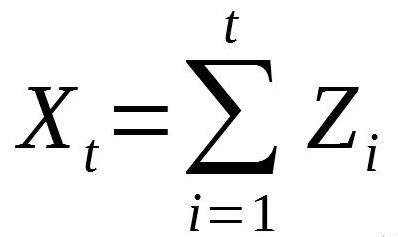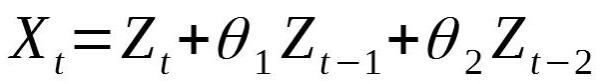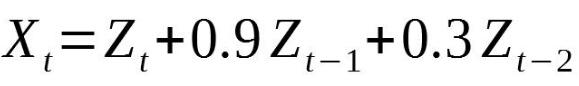了解隨機游走模型和移動平均過程(Python)
在本文中,我將介紹兩個能夠對時間序列進行建模的模型:隨機游走和移動平均過程。
隨機游走模型
隨機游走模型由以下公式表示:
換句話說,當前時刻t的位置是前一時刻(t-1)的位置與噪聲(用z表示)之和。這里我們假設噪聲是正態分布的(均值為0,方差為1)。
我們從0開始隨機游走,也就是說,任何時間點都是該時間之前所有噪聲的和。數學上表示為:
讓我們在Python中模擬隨機游走。
首先,我們導入所需的Python庫:
- from statsmodels.graphics.tsaplots import plot_acf
- from statsmodels.tsa.arima_process import ArmaProcess
- from statsmodels.tsa.stattools import acf
- import matplotlib.pyplot as plt
- import numpy as np
- %matplotlib inline
然后,我們生成一個包含1000個數據點的數據集。起點是0,我們將隨機噪聲添加到上一個點以生成下一個點:
- steps = np.random.standard_normal(1000)
- steps[0]=0
- random_walk = np.cumsum(steps)
繪制數據集的Python代碼如下:
- plt.figure(figsize=[10, 7.5]); # Set dimensions for figure
- plt.plot(random_walk)
- plt.title("Simulated Random Walk")
- plt.show()
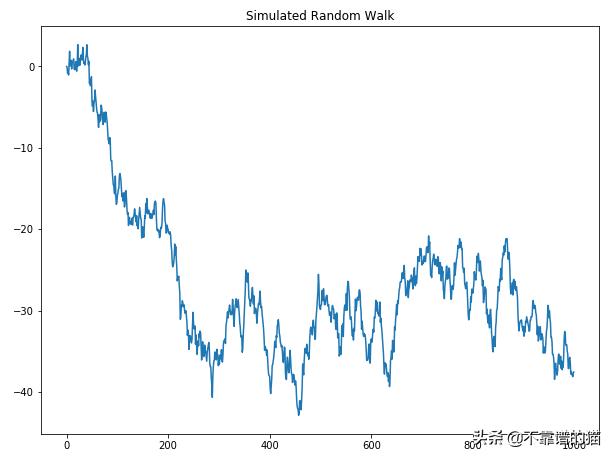
模擬隨機游走
你的隨機行走可能與上面的圖不同,因為噪聲是隨機的。
現在,讓我們看看我們的隨機游走的自相關圖(或相關圖):
- random_walk_acf_coef = acf(random_walk)
- plot_acf(random_walk, lags=20);
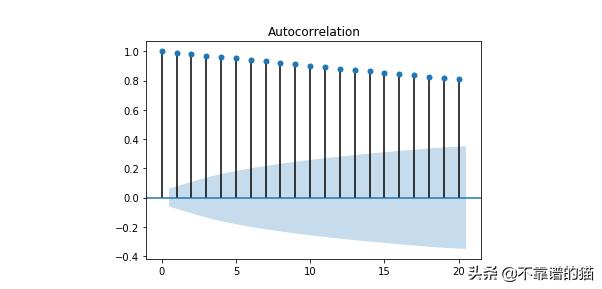
隨機游走的相關圖
不管你的隨機游走看起來像什么,你都應該得到一個非常相似的相關圖。
現在,一切都指向數據集中的趨勢。我們可以改變這種趨勢嗎?答案是肯定的。
讓我們在Python中進行驗證。
- random_walk_diff = np.diff(random_walk, n=1)
然后我們繪制結果:
- plt.figure(figsize=[10, 7.5]); # Set dimensions for figure
- plt.plot(random_walk_diff)
- plt.title('Noise')
- plt.show()
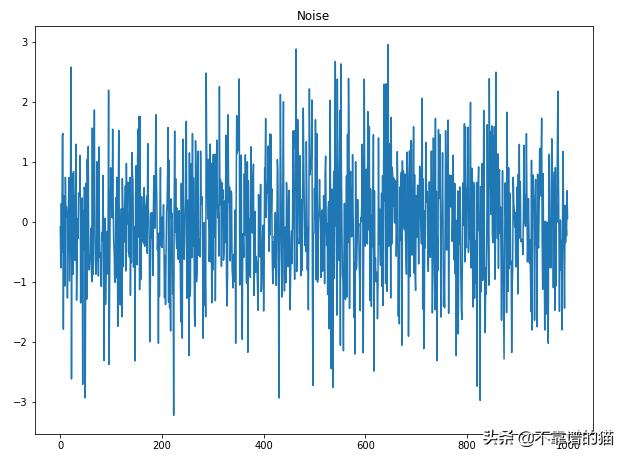
如您所見,上面的圖沒有趨勢,也沒有季節性,是一個完全隨機的過程。
查看相關圖的python代碼如下:
- plot_acf(random_walk_diff,lags = 20);
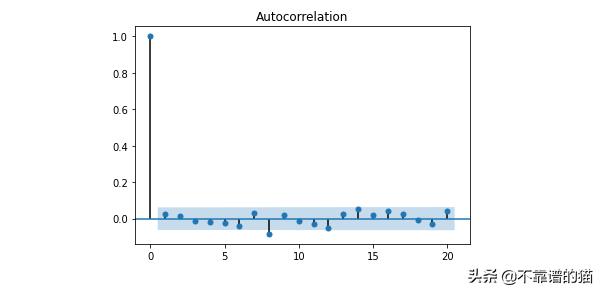
我們看到這是一個純隨機過程的相關圖,其中自相關系數在滯后1處下降。
移動平均過程
我們先來直觀了解一下什么是移動平均過程。
假設你把一塊石頭扔進一個池塘里,你要追蹤水面上一滴水的位置。當石頭撞擊水面時,會形成波紋,所以我們要跟蹤的水滴會上下移動。讓我們假設波紋只持續兩秒鐘,在這兩秒鐘之后,水面就會完全變平。
我們的水滴位置可以表示為:
上面的方程表示,X在t時刻的位置取決于t時刻的噪聲,加上t-1時刻的噪聲(有一定的權重THETA),加上t-2時刻的噪聲(有一定的權值)。
這被稱為二階移動平均過程,可以表示為MA(2)。
通用表示法是MA(q)。在上面的示例中,q = 2。
讓我們在Python中模擬此過程。具體來說,我們將模擬以下過程:
這是一個二階移動平均過程,我們指定了權重。您可以隨意更改權重,并對參數進行試驗。
我們從指定滯后開始,我們用的是2。
- ar2 = np.array([2])
然后,我們指定權重,權重為[1、0.9、0.3]。
- ma2 = np.array([1, 0.9, 0.3])
最后,我們模擬該過程并生成1000個數據點:
- MA2_process = ArmaProcess(ar2, ma2).generate_sample(nsample=1000)
現在,讓我們可視化該過程及其相關圖:
- plt.figure(figsize=[10, 7.5]); # Set dimensions for figure
- plt.plot(MA2_process)
- plt.title('Moving Average Process of Order 2')
- plt.show()
- plot_acf(MA2_process, lags=20);
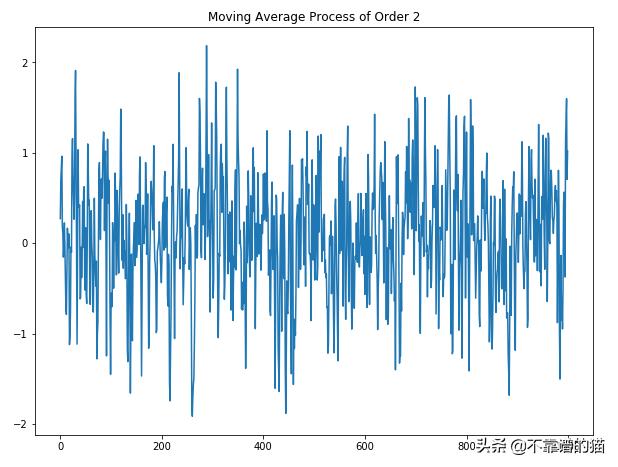
由于噪聲是隨機產生的,因此您的圖形可能與我的不同。但相關圖應與下圖類似:
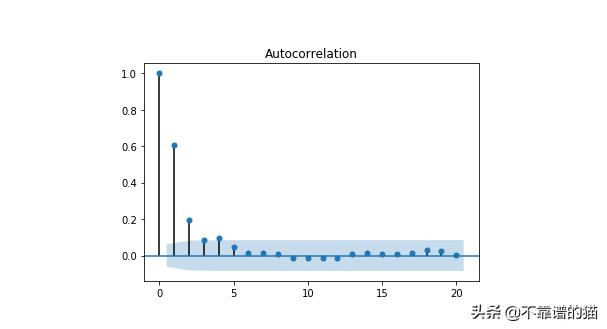
正如您所注意到的,相關性在滯后2之前是顯著的。這很有意義,因為我們指定了滯后為2。
這意味著您可以使用相關圖來推斷時間序列的滯后。如果您看到滯后q之后相關性并不顯著,那么您可以將時間序列建模為MA(q)過程。
最后
通過本文,您了解了隨機游走是什么以及如何對其進行模擬。此外,您還學習了移動平均過程,并了解了如何對其建模。