殺雞用牛刀，我們用機器學習方法來算圓的面積。

詢問任何人圓的面積是多少，他們都會告訴你不就是𝜋r²嗎。但如果你問他們為什么，他們很可能并不知道。

這是因為圓的面積公式的證明在大多數情況下要么不直觀，不令人滿意，要么充斥著積分等高級數學概念。

借鑒統計學習和機器學習的核心原理，我們可以使用蒙特卡羅模擬和多項式/二次回歸來創建基于計算的方法，以找到圓的面積公式。

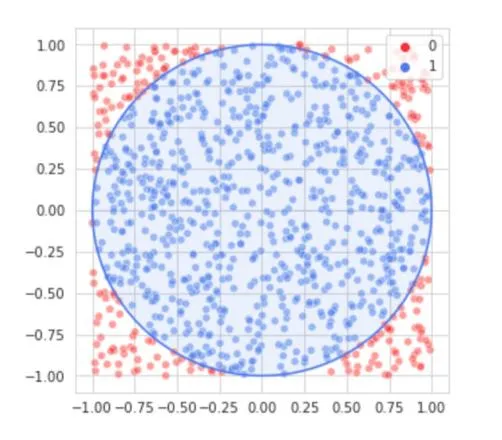
在不使用任何數學運算的情況下得出圓的面積，我們使用了蒙特卡羅方法。從探索不規則形狀的面積到預測股票市場的情況，都用到了蒙特卡羅方法。該方法的核心思想是引入隨機性，并測量系統對其作出的反饋，甚至可以在不了解系統原理的情況下獲得有效信息。

在使用蒙特卡羅來近似圓的面積時，我們先生成一些隨機坐標點 (x1,x2)，這兩個方向的坐標都是從負半徑值到正半徑值的均勻分布繪制得到的。我們在圓中放入 250,000 個這樣的坐標點，如中心極限定理(或大數定律)所描述的，研究所用的真實隨機樣例點越多，得到的結果就會越準確。

對于圓內的每一個點，我們可以引入一個落入圓內的點的數目的計數變量。在所有隨機點都被投入之后，圓內的點數除以總點數(該研究中為 250,000)的值就代表在正方形內圓的面積所占的分數。該正方形的邊長是圓的半徑的兩倍，因此正方形的面積是 4r²，其中 r 是圓的半徑。用 4r²乘之前得到的分數，就得到了圓的面積。通過蒙特卡羅方法，可以非常接近地得到圓的真實面積而無需數學計算公式。

道理很簡單，結果幾乎完全正確!

我們可以在給定半徑 r 的情況下找到任何圓的面積，但此時此刻我們還沒有歸納出圓的公式。為找到公式，我們需要創建一個二次方程式進行建模，該方程式需要一個半徑并嘗試輸出面積。為了正確地擬合方程，我們必須為每個半徑的蒙特卡洛近似面積收集數據。

import numpy as np 
from tqdm import tqdm #Just a progress bar indicator 
 
#Number of randomized points to generate for each approximation 
num_points = 250_000 
 
#Lists to store the radius and its corresponding area approximation 
radii = [] 
areas = [] 
 
#For each of the 500 equally spaced values between 1 and 100 inclusive: 
for radius in tqdm(np.linspace(1,100,500)): 
 
    #A counter for the number of points in the circle 
    in_circle = 0 
 
    for i in range(num_points): 
 
        #Generate an x and y coordinate from a uniform distribution bounded by a tangent box 
        xcoor = np.random.uniform(-radius,radius) 
        ycoor = np.random.uniform(-radius,radius) 
 
        #If the point is inside the circle, add one to in_circle 
        if xcoor**2 + ycoor**2 < radius**2: 
            in_circle += 1 
 
    #Get the fraction of the points that were inside the circle 
    area_frac = in_circle/num_points 
 
    #Append the approximated area and the radius 
    areas.append(area_frac*(4*(radius**2))) 
    radii.append(radius) 

而下一步就是寫一個擬合數據的二次項模型(回歸模型)，y =ax²。我們可以通過繪圖驗證數據為二次項，而不是三階或四階多項式。從本質上講，這是一個基礎的機器學習問題，因此再回顧一些基本術語：

• 模型參數：模型進行自動調整從而找到最佳參數，在這種情況下，參數為 a。如果具有 n 個參數，則該模型被稱為 n 維。我們所使用的最基本模型是一維的，而對圖像進行分類的深度神經網絡有可能具有數百萬個維度。
• 損失函數：損失函數是對當下模擬情況進行評估，并希望找到可以得到最低誤差度的參數集，從而使得損失函數最小化。比如某個參數值 j 的損失函數值為 3，而參數值 k 的損失函數值為 2，則理應選擇參數值 k。
• 平均絕對誤差(MAE)：我們將使用損失函數/錯誤度量，其原因是因為它易于使用且易于理解。給定當前參數(a)和模型預測值，而平均絕對誤差是指預測值與真實值之間平均相差有多大，較低的 MAE 意味著模型更適合數據。
• 學習率：為了優化參數，模型會在特定「方向」上逐漸調整參數。由于我們現在的模型僅優化一個參數(a)，因此僅需決定在一維平面上是增大或是減小參數值(任何變化都會產生較低的損失函數)。而模型在調整過程中的移動量稱為學習率。較高的學習速度意味著模型有可能短時間內就能得到一組效果較好的參數，但無法保證其準確度，而較低的學習率能夠獲得非常不錯的參數，并且擁有較高的準確度，唯一一點是需要大量的訓練時間。

有了這些變量，我們可以構建一個非常基礎簡單的程序，使得它對這些數據擬合：

• 把參數 coef(a)初始化為 0.1。
• 對于訓練周期中的每次迭代：
• 對 coef 提出兩條路徑;coef+lr 和 coef-lr，其中 lr 是學習率。
• 對使用 coef=coef+lr 的模型和使用 coef=coef-lr 的模型評估平均絕對誤差。

將 coef 設置為等于 coef+lr 和 coef-lr 中平均絕對誤差值較小的那個數字。

通過對平均絕對誤差的反復優化，模型最終將收斂出一個「最佳」的 coef 值(從而最大程度地降低平均絕對誤差)。這一思路正是機器學習的核心原理——通過反復地推斷、評估和修正，計算機可以「磨煉」出一套最優的參數。

coef = 0.1 #Initial coefficient value 
learning_rate = 0.00001 #How fast the model 'learns' 
iterations = 100000 #How many times we want the model to 'practice and correct' 
 
for i in tqdm(range(iterations)): #note - tqdm is just a progressbar 
 
    #Propose two path for the coefficient: 
    up_coef = coef + learning_rate #Move up 
    down_coef = coef - learning_rate #Or move down 
 
    #Store the predictions for a model using parameters up_coef and down_coef 
    up_pred = [] 
    down_pred = [] 
 
    #For each radius value in the previously created list radii: 
    for r in radii: 
 
        #Append the model using up_coef's and down_coef's prediction (a*r^2) 
        up_pred.append(up_coef*(r**2)) 
        down_pred.append(down_coef*(r**2)) 
 
    #Find the MAE. Both are converted to NumPy arrays for easy operation.     
    up_coef_mae = np.abs(np.array([up_pred])-np.array([areas])).mean() 
    down_coef_mae = np.abs(np.array([down_pred])-np.array([areas])).mean() 
 
    #If moving the coefficient down yields a lower (better) MAE:     
    if down_coef_mae < up_coef_mae: 
 
        #Set it equal to down_coef 
        coef = down_coef 
 
    #Otherwise (moving the coefficient up yields a lower (better) or equal MAE: 
    else: 
 
        #Set it equal to up_coef 
        coef = up_coef 

當我們查看訓練的 coef 值時，可以看到它等于π：

print(str(coef)[:5]) #first four digits of coefficient (decimal point counts as a character) 
[Output]: '3.141' 

當然，計算圓面積的公式很好記就是𝜋r²。無需使用微積分中的任何復雜的數學方法或其他證明，我們就能找到它的公式，并找到一種使用蒙特卡洛模擬和二次回歸找到𝜋值的方法。使用這種思路就可以找到計算圓面積的方法——當然也可以找到任何圖形的面積計算公式——橢圓、心形、二維的烏龜形狀——只要參數可以說明它的輪廓。

近年來，計算機已經接手開始解決復雜的高可變數學問題，計算圓面積只是其中的一個簡單的示例。如果想要更復雜、更具開創性的，那當然是四色定理了(每個無外飛地的地圖都可以用不多于四種顏色來染色，且不會有兩個鄰接的區域顏色相同)。這是第一個由計算機先生成證明，又被數學家廣泛接受的成果。

借助計算機，人類可以探索以往無法嘗試進入的，極其復雜的數學領域。

原文鏈接：https://medium.com/swlh/finding-the-formula-for-circle-area-without-using-any-math-898cbee70253

【本文是51CTO專欄機構“機器之心”的原創譯文，微信公眾號“機器之心( id: almosthuman2014)”】 

戳這里，看該作者更多好文