沒有完整圖時,如何使用圖深度學習?
流形學習,自 2000 年在著名的科學雜志《Science》被首次提出以來,已成為信息科學領域的研究熱點。可能很多人會問,流形學習有什么用呢?首先流形學習可以作為一種數據降維的方式,第二,流形能夠刻畫數據的本質。其主要代表方法有等距映射、局部線性嵌入等。那么,具有流形學習 2.0 之稱的潛圖學習方法如何呢?
自從神經網絡提出以來,其在人臉識別、語音識別等方面表現出卓越的性能。以前需要人工提取特征的機器學習任務,現在通過端到端的方法就能解決。
傳統的深度學習方法在提取歐氏空間數據(比如圖片是規則的正方形柵格,語音數據是一維序列)的特征方面取得了巨大的成功。但是,在許多任務中,數據不具備規則的空間結構,即非歐氏空間下的數據,如電子交易、推薦系統等抽象出來的圖譜,圖譜中每個節點與其他節點的連接不是固定的。在經典的 CNN、RNN 等框架無法解決或效果不好的情況下,圖神經網絡應運而生。
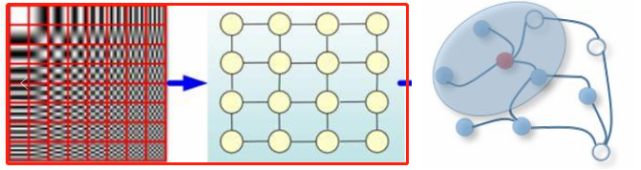
圖左(紅框):歐氏空間數據;圖右:非歐氏空間數據。
圖神經網絡利用關系歸納偏置來處理以圖形式出現的數據。然而,在許多情況下,并沒有現成的圖。那么圖深度學習適用于這類情形嗎?本文將介紹潛圖學習(latent graph learning)和更早的流形學習(manifold learning)。
潛圖學習
在過去的幾年里,人們對使用機器學習方法處理圖結構數據產生了濃厚的興趣。這類數據自然也出現在許多應用中,例如社會科學(如 Twitter 或 Facebook 上的用戶 Follow 圖)、化學(分子可被建模為鍵連接的原子圖)或生物學(不同生物分子之間的相互作用通常被建模為相互作用組圖)。圖神經網絡(GNN)是一種特別流行的圖學習方法,該算法通過在相鄰節點之間交換信息的共享參數進行局部操作。
然而,在某些情況下,沒有現成的圖可以作為輸入。在生物學中尤其如此,諸如蛋白質 - 蛋白質相互作用的圖只有部分已知,因為發現蛋白質相互作用的實驗費用昂貴,而且噪聲很大。因此,研究者從數據中推斷出圖并在其上應用 GNN,并將其稱為「潛圖學習」。潛圖學習特定于應用,并針對下游任務進行了優化。此外,有時這樣的圖可能比任務本身更重要,因為它可以傳達關于數據的重要洞察,并提供解釋結果的方法。
潛圖學習是學習具有空邊集的圖。在這一設置中,輸入為高維特征空間中的點云。在集合上進行深度學習的方法(如 PointNet)對每個點應用共享可學習 point-wise 函數,與之不同,潛圖學習還尋求跨點信息傳遞。
DGCNN
點云動態圖卷積神經網絡(DGCNN)是第一個這樣的架構,該架構由麻省理工學院的 Yue Wang 開發。受計算機圖形學中涉及 3D 點云分析問題的啟發,該架構將圖用作點云下局部光滑流形結構的粗略表示。Yue 的一個重要發現是,圖在整個神經網絡中不需要保持不變,事實上,它可以而且應該動態更新——因此該方法被命名為 DGCNN。
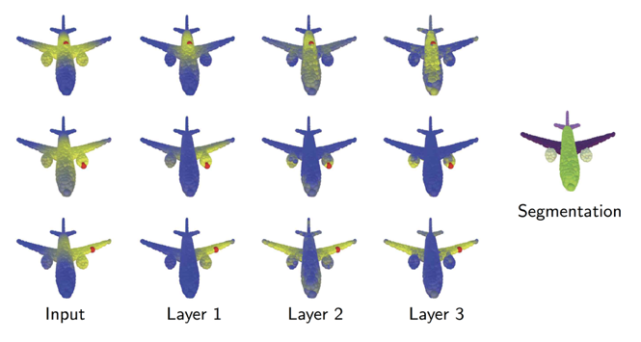
DGCNN 動態構造一個用于特征擴散的 k 近鄰圖。圖依賴于任務,并在每個層之后更新。這幅圖(摘自 [4])展示了與紅點的距離(黃色代表更近的點),表明在分割任務中,更深層次的圖捕捉語義關系而不是幾何關系,如成對的機翼、發動機等。
DGM
DGCNN 的一個局限性是用相同的空間來構造圖和圖上的特征。Anees Kazi 和 Luca Cosmo 提出了一種新的架構——可微圖模塊(DGM),通過對圖和特征構造進行解耦來擴展 DGCNN,如下圖所示:
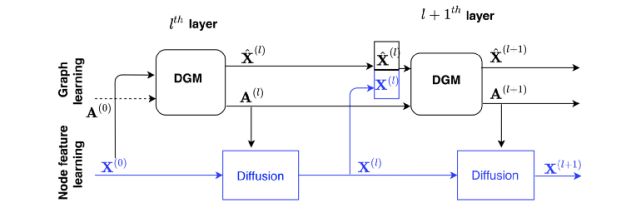
DGM 提供了一種基于輸入數據構造圖并在圖上擴散特征的機制。(圖源:[5])
當應用于醫學領域問題時,DGM 顯示出優秀的結果,例如根據腦成像數據預測疾病。在這些任務中,研究者獲取到多個患者的電子健康記錄,包括人口統計學特征(如年齡、性別等)和大腦成像特征,并嘗試預測患者是否患有神經系統疾病。之前的工作展示了 GNN 在這類任務中的應用,方法是在一個根據人口統計學特征手工構建的「病人圖」上進行特征擴散。而 DGM 提供了學習圖的優勢,可以傳達某些特征在特定診斷任務中是如何相互依賴的。其次,DGM 在點云分類任務中也擊敗了 DGCNN,不過優勢很小。
流形學習
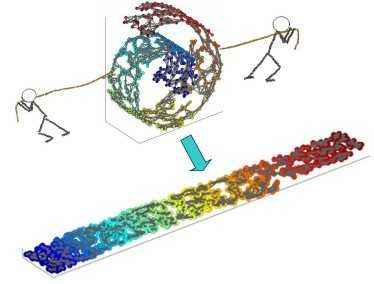
DGCNN 和 DGM 在概念上與流形學習或非線性降維算法相似,流形學習很早就已出現并流行,且目前仍用于數據可視化。流形學習方法的基本假設是數據具有內在的低維結構。雖然數據可以在數百甚至數千維的空間中表示,但它卻只有幾個自由度,示例如下:
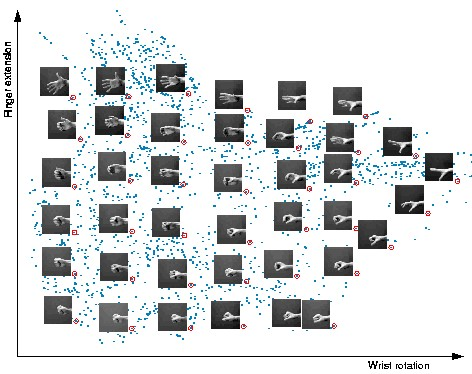
雖然這個數據集中的手部圖像是高維的(64x64 像素構成 4096 個維度),但它們本質上是低維的,可以用兩個自由度來解釋:手腕旋轉和手指伸展。流形學習算法能夠捕捉數據集的這種內在低維結構,并將其在歐幾里德空間中進行表示。(圖源 [9])
再比如球面上的一點(即三維歐式空間上的點),可以用三元組來表示其坐標:
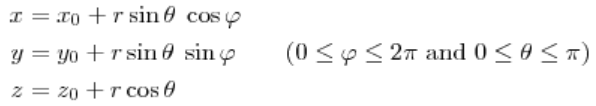
但事實上這個三維坐標只有兩個變量 θ 和 φ,也可以說它的自由度為 2,正好對應了它是一個二維的流形。
流形學習的目的是捕捉這些自由度,并將數據的維數降至其固有維數。流形學習與 PCA 等線性降維方法的重要區別在于,由于數據的非歐幾里德結構,我們可能無法通過線性投影恢復流形。如下圖所示,線性降維(左)為線性降維,流形學習(右)為非線性降維。
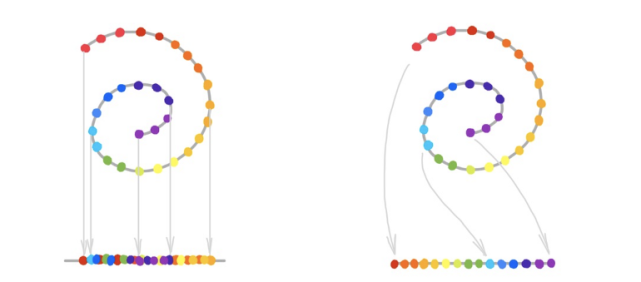
流形學習算法在恢復「流形」方法上各不相同,但它們有一個共同的藍圖。
首先,創建一個數據表示,通過構造一個 k 近鄰圖來獲取其局部結構。其次,計算數據的低維表示(嵌入),并試圖保留原始數據的結構。這是大多數流形學習方法的區別所在。這種新的表示將原來的非歐幾里德結構「展平」成一個更容易處理的歐幾里德空間。第三,一旦計算出表示,就會對其應用機器學習算法(通常是聚類)。
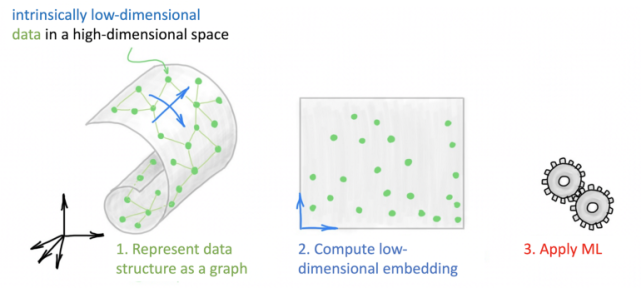
多種流形學習方法的藍圖:首先,將數據表示為圖;其次,計算該圖的低維嵌入;第三,將 ML 算法應用于這種低維表示。
這其中面臨的一項挑戰是圖構建與 ML 算法的分離,有時需要精確的參數調整(例如鄰域數或鄰域半徑),以確定如何構建圖才能使下游任務正常運行。流形學習算法更嚴重的缺點或許是:數據很少表示為低維的原始形式。例如,在處理圖像時,必須使用各種人工制定的特征提取技術作為預處理步驟。
圖深度學習提供了一種現代方法,即用單個圖神經網絡代替上文提到的三個階段。例如,在 DGCNN 或 DGM 中,圖的構造和學習是同一架構的一部分:
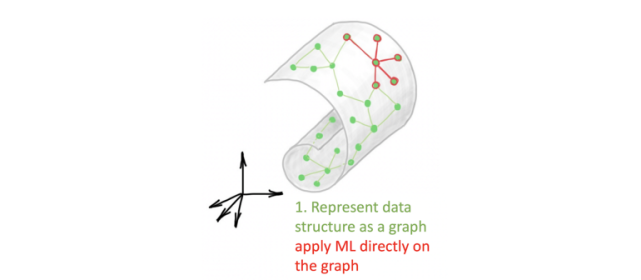
潛圖學習可以看作是流形學習問題的一種現代設置,在這里,圖被學習并用作某些下游任務優化的端到端 GNN pipeline 的一部分。
這種方法的吸引力在于:將單個數據點和它們所在的空間結合在相同的 pipeline 中。在圖像的例子中,我們可以使用傳統的 CNN 從每個圖像中提取視覺特征,并使用 GNN 來建模它們之間的關系。
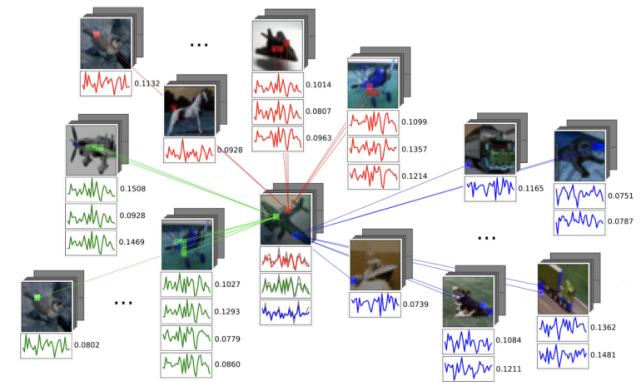
PeerNet 是標準 CNN 中基于圖的正則化層,可聚合來自多個圖像的相似像素,從而降低對對抗性擾動的敏感性。(圖源 [12])
潛圖學習的其它應用
潛圖學習還有許多其他有趣的應用。
第一是少樣本學習:利用基于圖的方法從少量樣本中進行歸納(重點:只需要少量帶有標注的樣本)。在計算機視覺中,數據標注量從幾千到上萬不等,成本很高,因此少樣本學習變得越來越重要。
第二是生物學領域:人們經常通過實驗觀察生物分子如蛋白質的表達水平,并試圖重建它們的相互作用和信號網絡。
第三是對物理系統的分析:其中圖可以描述多個對象之間的交互作用。尤其是處理復雜粒子相互作用的物理學家,最近對基于圖的方法表現出了濃厚的興趣。
第四是 NLP 問題:在 NLP 領域中,圖神經網絡可以看作是 transformer 架構的泛化。所提到的許多問題也提出了在圖結構中加入先驗知識,這一結構在很大程度上仍然是開放的:例如,人們可能希望強迫圖遵守某些構造規則或與某些統計模型兼容。
潛圖學習,雖然不是全新的領域,但它為舊問題提供了新的視角。對于圖機器學習問題而言,這無疑是一個有趣的設置,為 GNN 研究人員提供了新的方向。