數據結構與算法系列 - 深度優先和廣度優先
前言
數據結構與算法系列(完成部分):
- 時間復雜度和空間復雜度分析
- 數組的基本實現和特性
- 鏈表和跳表的基本實現和特性
- 棧、隊列、優先隊列、雙端隊列的實現與特性
- 哈希表、映射、集合的實現與特性
- 樹、二叉樹、二叉搜索樹的實現與特性
- 堆和二叉堆的實現和特性
- 圖的實現和特性
- 遞歸的實現、特性以及思維要點
- 分治、回溯的實現和特性
- 深度優先搜索、廣度優先搜索的實現和特性
- 貪心算法的實現和特性
- 二分查找的實現和特性
- 動態規劃的實現及關鍵點
- Tire樹的基本實現和特性
- 并查集的基本實現和特性
- 剪枝的實現和特性
- 雙向BFS的實現和特性
- 啟發式搜索的實現和特性
- AVL樹和紅黑樹的實現和特性
- 位運算基礎與實戰要點
- 布隆過濾器的實現及應用
- LRU Cache的實現及應用
- 初級排序和高級排序的實現和特性
- 字符串算法
PS:大部分已經完成在公眾號或者GitHub上,后面陸續會在頭條補充鏈接(不允許有外部鏈接)
本篇討論深度優先搜索和廣度優先搜索相關內容。
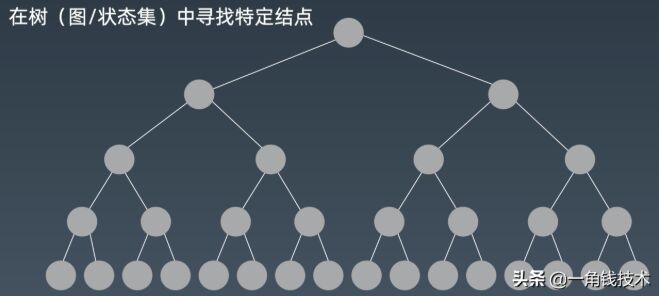
關于搜索&遍歷
對于搜索來說,我們絕大多數情況下處理的都是叫 “所謂的暴力搜索” ,或者是說比較簡單樸素的搜索,也就是說你在搜索的時候沒有任何所謂的智能的情況在里面考慮,很多情況下它做的一件事情就是把所有的結點全部遍歷一次,然后找到你要的結果。
基于這樣的一個數據結構,如果這個數據結構本身是沒有任何特點的,也就是說是一個很普通的樹或者很普通的圖。那么我們要做的一件事情就是遍歷所有的結點。同時保證每個點訪問一次且僅訪問一次,最后找到結果。
那么我們先把搜索整個先化簡情況,我們就收縮到在樹的這種情況下來進行搜索。
如果我們要找到我們需要的一個值,在這個樹里面我們要怎么做?那么毫無疑問就是從根這邊開始先搜左子樹,然后再往下一個一個一個一個點走過去,然后走完來之后再走右子樹,直到找到我們的點,這就是我們所采用的方式。
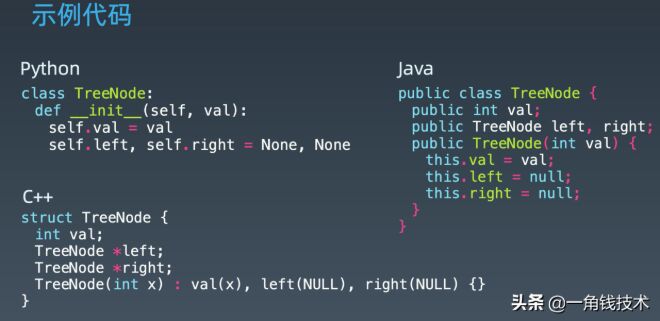
再回到我們數據結構定義,它只有左子樹和右子樹。
我們要實現這樣一個遍歷或者搜索的話,毫無疑問我們要保證的事情就是
- 每個結點都要訪問一次
- 每個結點僅僅要訪問一次
- 對于結點訪問的順序不限
- 深度優先:Depth First Search
- 廣度優先:Breadth First Search
僅訪問一次的意思就是代表我們在搜索中,我們不想做過多無用的訪問,不然的話我們的訪問的效率會非常的慢。
當然的話還可以有其余的搜索,其余的搜索的話就不再是深度優先或者廣度優先了,而是按照優先級優先 。當然你也可以隨意定義,比如說從中間優先類似于其他的東西,但只不過的話你定義的話要有現實中的場景。所以你可以認為是一般來說就是深度優先、廣度優先,另外的話就是優先級優先。按照優先級優先搜索的話,其實更加適用于現實中的很多業務場景,而這樣的算法我們一般把它稱為啟發式搜索,更多應用在深度學習領域。而這種比如說優先級優先的話,在很多時候現在已經應用在各種推薦算法和高級的搜索算法,讓你搜出你中間最感興趣的內容,以及每天打開抖音、快手的話就給你推薦你最感興趣的內容,其實就是這個原因。
深度優先搜索(DFS)
遞歸寫法
遞歸的寫法,一開始就是遞歸的終止條件,然后處理當前的層,然后再下轉。
- 那么處理當前層的話就是相當于訪問了結點 node,然后把這個結點 node 加到已訪問的結點里面去;
- 那么終止條件的話,就是如果這個結點之前已經訪問過了,那就不管了;
- 那么下轉的話,就是走到它的子結點,二叉樹來說的話就是左孩子和右孩子,如果是圖的話就是連同的相鄰結點,如果是多叉樹的話這里就是一個children,然后把所有的children的話遍歷一次。
1.二叉樹模版
Java 版本
- //C/C++
- //遞歸寫法:
- map<int, int> visited;
- void dfs(Node* root) {
- // terminator
- if (!root) return ;
- if (visited.count(root->val)) {
- // already visited
- return ;
- }
- visited[root->val] = 1;
- // process current node here.
- // ...
- for (int i = 0; i < root->children.size(); ++i) {
- dfs(root->children[i]);
- }
- return ;
- }
Python 版本
- #Python
- visited = set()
- def dfs(node, visited):
- if node in visited: # terminator
- # already visited
- return
- visited.add(node)
- # process current node here.
- ...
- for next_node in node.children():
- if next_node not in visited:
- dfs(next_node, visited)
C/C++ 版本
- //C/C++
- //遞歸寫法:
- map<int, int> visited;
- void dfs(Node* root) {
- // terminator
- if (!root) return ;
- if (visited.count(root->val)) {
- // already visited
- return ;
- }
- visited[root->val] = 1;
- // process current node here.
- // ...
- for (int i = 0; i < root->children.size(); ++i) {
- dfs(root->children[i]);
- }
- return ;
- }
JavaScript版本
- visited = set()
- def dfs(node, visited):
- if node in visited: # terminator
- # already visited
- return
- visited.add(node)
- # process current node here.
- ...
- for next_node in node.children():
- if next_node not in visited:
- dfs(next_node, visited)
2.多叉樹模版
- visited = set()
- def dfs(node, visited):
- if node in visited: # terminator
- # already visited
- return
- visited.add(node)
- # process current node here.
- ...
- for next_node in node.children():
- if next_node not in visited:
- dfs(next_node, visited)
非遞歸寫法
Python版本
- #Python
- def DFS(self, tree):
- if tree.root is None:
- return []
- visited, stack = [], [tree.root]
- while stack:
- node = stack.pop()
- visited.add(node)
- process (node)
- nodes = generate_related_nodes(node)
- stack.push(nodes)
- # other processing work
- ...
C/C++版本
- //C/C++
- //非遞歸寫法:
- void dfs(Node* root) {
- map<int, int> visited;
- if(!root) return ;
- stack<Node*> stackNode;
- stackNode.push(root);
- while (!stackNode.empty()) {
- Node* node = stackNode.top();
- stackNode.pop();
- if (visited.count(node->val)) continue;
- visited[node->val] = 1;
- for (int i = node->children.size() - 1; i >= 0; --i) {
- stackNode.push(node->children[i]);
- }
- }
- return ;
- }
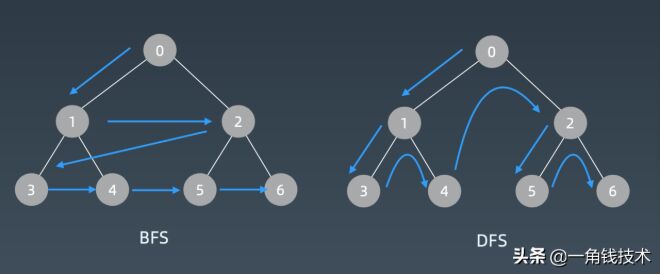
遍歷順序
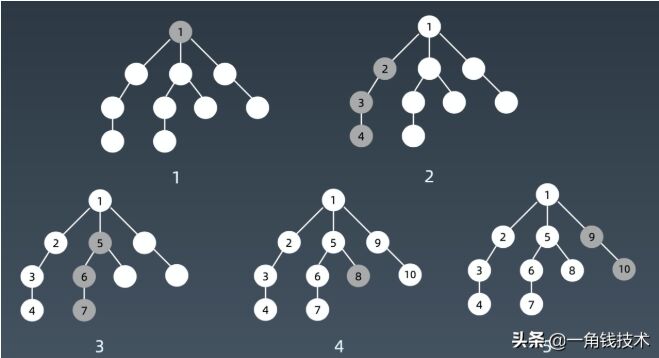
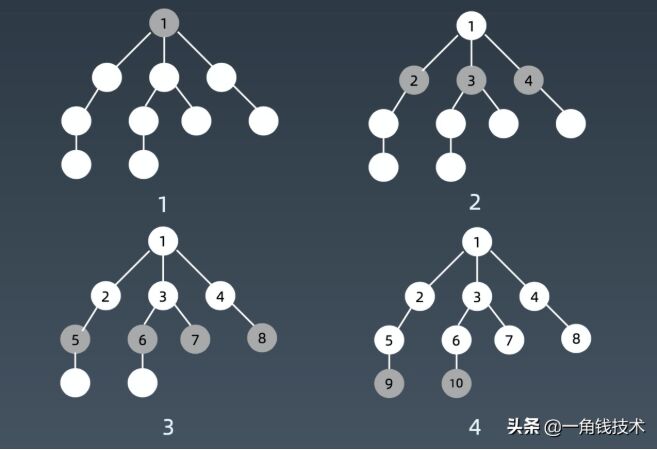
我們看深度優先搜索或者深度優先遍歷的話,它的整個遍歷順序毫無疑問根節點 1 永遠最先開始的,接下來往那個分支走其實都一樣的,我們簡單起見就是從最左邊開始走,那么它深度優先的話就會走到底。
參考多叉樹模版我們可以在腦子里面或者畫一個圖把它遞歸起來的話,把遞歸的狀態樹畫出來,就是這么一個結構。
- 就比如說它開始剛進來的話,傳的是 root 的話,root 就會先放到 visited 里面,表示 root 已經被 visit,被 visited之后就從 root.childern里面找 next_node,所有它的next_node都沒有被訪問過的,所以它就會先訪問最左邊的這個結點,這里注意當它最左邊這個結點先拿出來了,判斷沒有在 visited里面,因為除了 root之外其他結點都沒有被 visited過,那么沒有的話它就直接調dfs,next_node 就是把最左邊結點放進去,再把 visited也一起放進去。
- 遞歸調用的一個特殊,它不會等這個循環跑完,它就直接推進到下一層了,也就是當前夢境的話這里寫了一層循環,但是在第一層循環的時候,我就要開始下鉆到新的一層夢境里面去了。
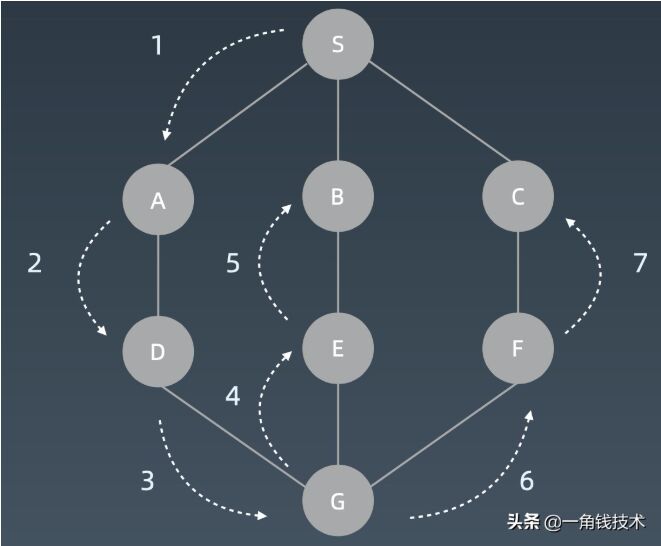
圖的遍歷順序
廣度優先搜索(BFS)
廣度優先遍歷它就不再是用遞歸也不再是用棧了,而是用所謂的隊列。你可以把它想象成一個水滴,滴到1這個位置,然后它的水波紋一層一層一層擴散出去就行了。
兩者對比
BFS代碼模板
- //Java
- public class TreeNode {
- int val;
- TreeNode left;
- TreeNode right;
- TreeNode(int x) {
- val = x;
- }
- }
- public List<List<Integer>> levelOrder(TreeNode root) {
- List<List<Integer>> allResults = new ArrayList<>();
- if (root == null) {
- return allResults;
- }
- Queue<TreeNode> nodes = new LinkedList<>();
- nodes.add(root);
- while (!nodes.isEmpty()) {
- int size = nodes.size();
- List<Integer> results = new ArrayList<>();
- for (int i = 0; i < size; i++) {
- TreeNode node = nodes.poll();
- results.add(node.val);
- if (node.left != null) {
- nodes.add(node.left);
- }
- if (node.right != null) {
- nodes.add(node.right);
- }
- }
- allResults.add(results);
- }
- return allResults;
- }
- # Python
- def BFS(graph, start, end):
- visited = set()
- queue = []
- queue.append([start])
- while queue:
- node = queue.pop()
- visited.add(node)
- process(node)
- nodes = generate_related_nodes(node)
- queue.push(nodes)
- # other processing work
- ...
- // C/C++
- void bfs(Node* root) {
- map<int, int> visited;
- if(!root) return ;
- queue<Node*> queueNode;
- queueNode.push(root);
- while (!queueNode.empty()) {
- Node* node = queueNode.top();
- queueNode.pop();
- if (visited.count(node->val)) continue;
- visited[node->val] = 1;
- for (int i = 0; i < node->children.size(); ++i) {
- queueNode.push(node->children[i]);
- }
- }
- return ;
- }
- //JavaScript
- const bfs = (root) => {
- let result = [], queue = [root]
- while (queue.length > 0) {
- let level = [], n = queue.length
- for (let i = 0; i < n; i++) {
- let node = queue.pop()
- level.push(node.val)
- if (node.left) queue.unshift(node.left)
- if (node.right) queue.unshift(node.right)
- }
- result.push(level)
- }
- return result
- };