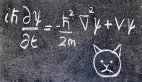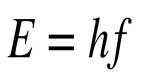[[347629]]

本文經AI新媒體量子位（公眾號ID:QbitAI）授權轉載，轉載請聯系出處。

 只要解出薛定諤方程，你就能預測分子的化學性質。但現實很骨感，迄今為止，科學家只能精確求解一個電子的氫原子，即使是只有兩個電子的氦原子都無能為力。

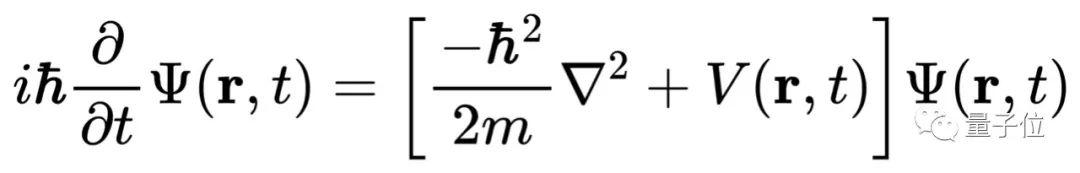
原因是有兩個以上電子組成的薛定諤方程實在太復雜，根本無法精確求解。

既然找不到精確解，科學家們希望能找到一種實用的近似解求法，只要結果足夠近似，也能預測原子或分子的行為。

近日，DeepMind開源了一個“費米網絡”（FermiNet），用來求解分子的電子行為，在30個電子的有機分子上也達到了很高的精度。文章結果發表在期刊Physical Review Research上。

為什么叫費米網絡

在量子力學中，電子沒有精確的位置，我們只能從波函數預測電子在空間中出現的概率，也就是電子云。

比如氫原子的電子云就有以下幾種形態。

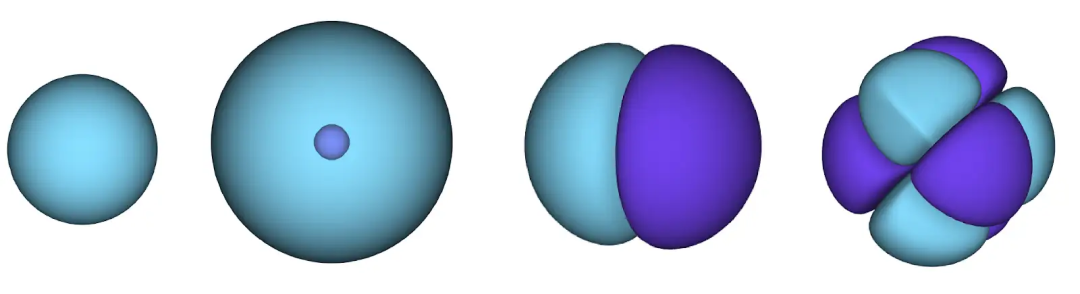
曲面內表示電子出現的高概率區域。藍色區域波函數為正，紫色區域波函數為負。（注：波函數平方表示電子出現的概率）

誤差小于0.5%即可預測分子的能量，但這對于化學家來說遠遠不夠，要準確預測分子的形狀和化學性質，需要0.001%的精度，相當于以毫米精度測量足球場寬度。

電子在分子中不僅受到原子核的吸引力、其他電子的斥力，還遵循著量子力學中的費米-狄拉克統計：如果兩個電子交換狀態，波函數要反號。

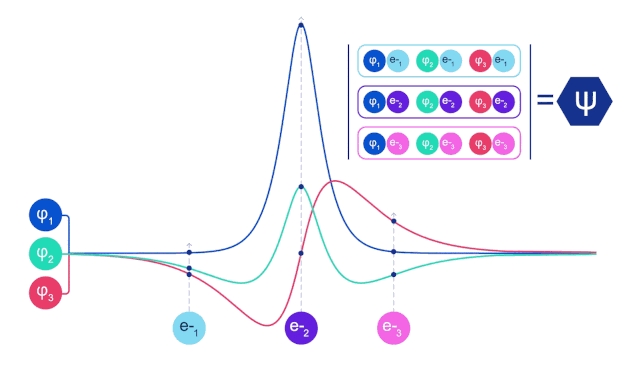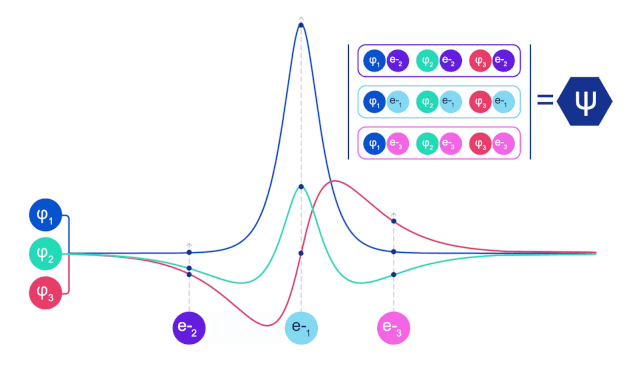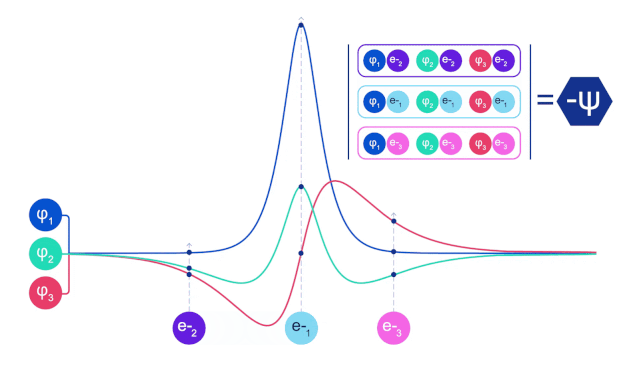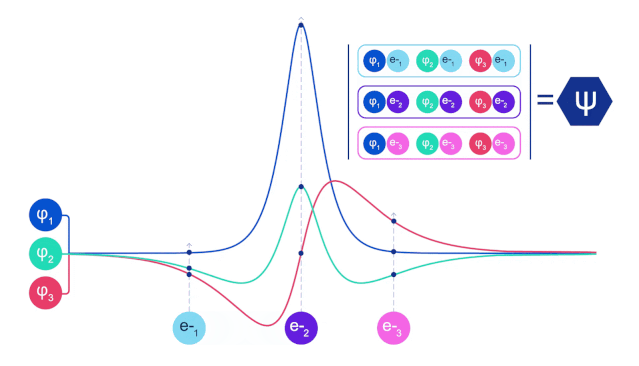
這也意味著兩個電子的狀態不可能完全相同，否則波函數為0。這在物理中叫做“泡利不相容原理”。

費米網絡正是從這個基本物理原理出發，因此DeepMind將其命名為FermiNet。

交換后符號相反，這可能會讓你想到線性代數中的行列式。行列式任意兩行交換，輸出結果就要乘以-1。

物理學家也是這樣想的，他們用所謂“Slater行列式”來表示電子波函數，但實際情況比Slater行列式要復雜得多，為了更精確表示電子行為，往往需要幾百萬個Slater行列式的線性組合。

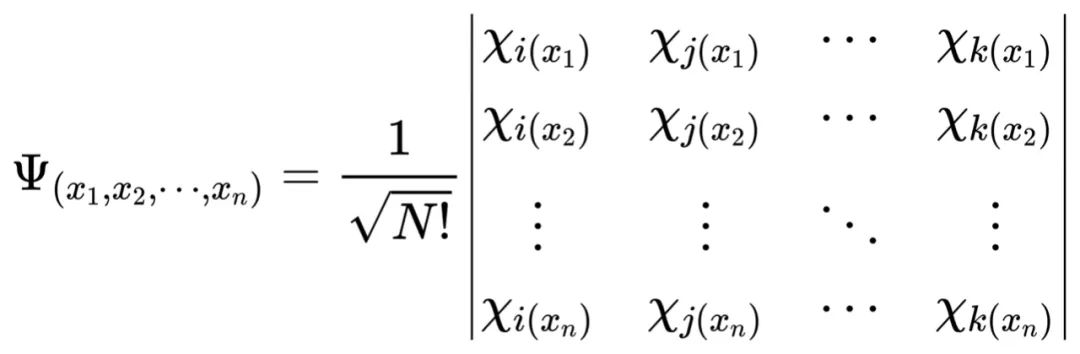
工作原理

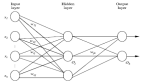
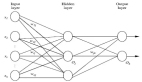
與函數線性組合相比，神經網絡在表示復雜函數時往往更具有優勢。

在構造FermiNet之初，研究人員就把泡利不相容原理作為第一性原理引入神經網絡。

在FermiNet中，每個電子都有單獨的信息流。不僅如此，他們將網絡每一層所有流平均化，然后傳遞給下一層的每一流。這樣，這些流就具有正確的反對稱性要求。

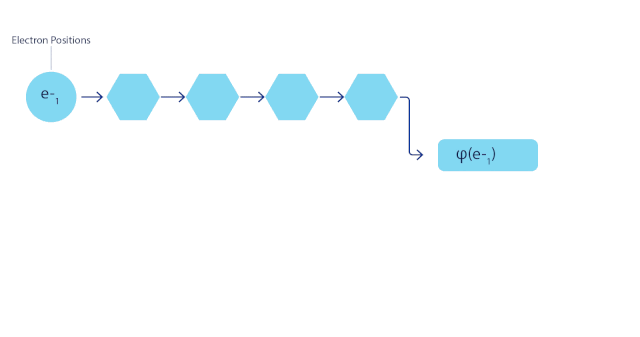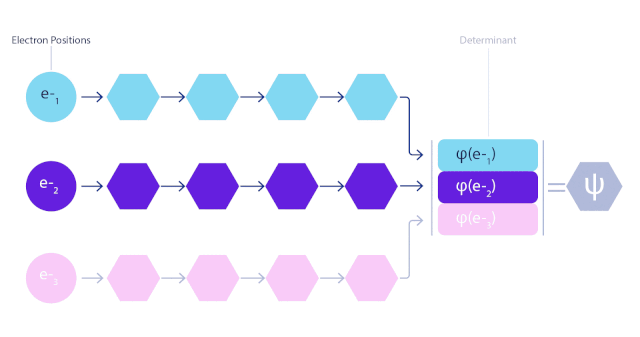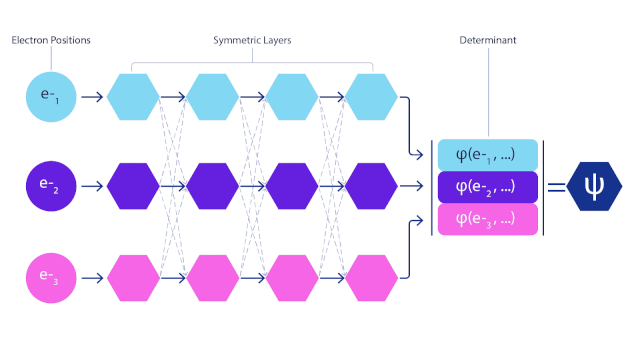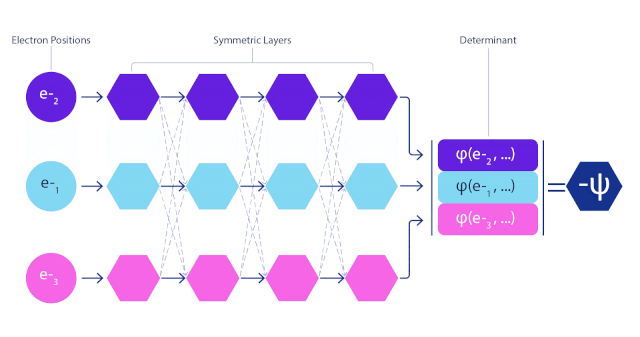
而且在FermiNet行列式中的每個元素都包含所有電子，效率遠遠超出波函數只有單個電子的情況。

與Slater行列式不同，FermiNet是通用函數逼近器，如果神經網絡層變得足夠寬，則可以無限逼近真實波函數。

這意味著，如果我們正確地訓練這些網絡，它們應該能夠將幾乎完全精確的解擬合到薛定諤方程。

訓練是通過最小化系統的能量來擬合FermiNet。FermiNet用蒙特卡洛方法隨機選擇電子構型，在每個電子排列中局部評估能量，累加每個排列的貢獻，并將其最小化。

實驗結果

研究人員將FermiNet用在具有10個電子以內的原子上，能量精度均在99.8%左右。

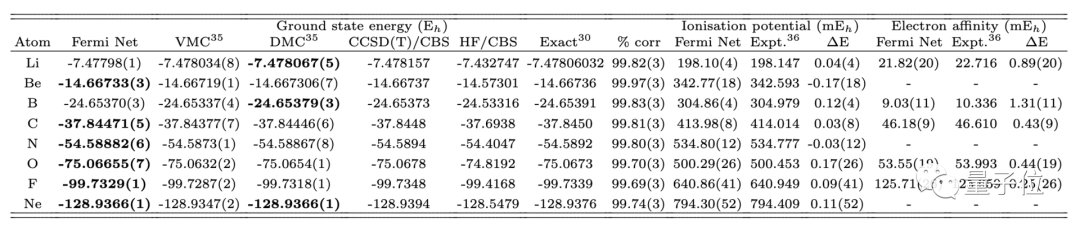
對于30個電子的環二丁烷，FermiNet算出的能量達到了97%的精度，雖然精度不是很高，但DeepMind表示，作為一種“便宜但不夠準確”的方法，這是巨大的成就。

現在FermiNet已經在GitHub上開源，代碼基于TensorFlow實現，如果你想用它算一算氫分子，不妨試試這串代碼：

經過100次迭代后，該程序會輸出一個氫原子波函數文件。官方建議最好用GPU來運行，因為他們計算乙烯分子就用8個GPU花2天時間才算出。

除了研究電子外，DeepMind還將神經網絡用于其他基礎科學研究，比如蛋白質折疊、玻璃態動力學、晶格量子色動力學等。