高數有救了!神經網絡不到一秒就能求解偏微分方程
隨著任務數量的增加,使用當前計算方法來構建通用的日常機器人的成本變得過高,人們正在快速尋求一種解決辦法。我們都希望通用機器人可以執行一系列復雜的任務,例如清潔,維護和交付
你的「高等數學」還好嗎?
微分方程是數學中重要的一課。所謂微分方程,就是含有未知函數的導數。一般凡是表示未知函數、未知函數的導數與自變量之間關系的方程,就叫做微分方程。
如果未知函數是一元函數的,就叫做常微分方程;
如果未知函數是多元的,就叫做偏微分方程。
偏微分方程擁有廣泛的應用場景,模擬客機在空中的飛行姿勢,地震波在地球上的仿真,傳染病在人群中擴散的過程,研究基本力和粒子之間的相互作用等場景,工程師、科學家和數學家們都訴諸于偏微分方程來描述涉及許多獨立變量的復雜現象。
然而,偏微分方程的求解過程卻是異常艱難的,尤其對于計算機來說,只能以最笨拙的方法去求解。
對于特別復雜的偏微分方程,可能需要數百萬個CPU小時才能求解出來一個結果。隨著問題越來越復雜,從設計更優秀的火箭發動機到模擬氣候變化,科學家們需要一個更「聰明」的求解方法。
或許,可以試試神經網絡?
最近,研究人員通過神經網絡實驗證明了它可以比傳統的偏微分方程求解器更快地求出近似解。
更牛的是,經過訓練的網絡,無需再次訓練就可以解決一類偏微分方程。
通常,神經網絡將數據從一個有限維空間(例如,圖像的像素值)映射或轉換為另一個有限維空間(例如,將圖像分類的數字,例如1代表貓,2代表狗)。
求解偏微分方程的神經網絡從無窮大的空間映射到無窮大的空間。
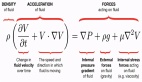
偏微分方程的用處和他們的復雜性相伴而生,例如,我們想要觀察空氣在飛機機翼附近的流動二維透視圖,建模人員想知道流體在空間中任何一點(也稱為流場)以及在不同時間的速度和壓力的話,就需要用到偏微分方程。
考慮到能量、質量和動量守恒定律,特定的偏微分方程,即Navier-Stokes方程可以對這種流體流動進行建模。
在這種情況下,解決方案可能是一個特定公式,可以讓開發人員在不同時間計算流場的狀態。
偏微分方程常常是很復雜的,以至于無法提供通用的分析解決方案。對于Navier-Stokes方程的最通用形式尤其如此:數學家尚未證明是否存在唯一解,更不用說實際地通過分析找到它們了。
在這些情況下,建模者會轉向數值方法,將偏微分方程轉換為一組易于處理的代數方程,假定這些方程可保持很小的空間和時間增量。
在超級計算機上,用數值方式解決復雜的偏微分方程可能要花費數月的時間。
而且,如果初始條件或邊界條件或所研究系統的幾何形狀(例如機翼設計)發生了變化,就必須重新開始求解。同樣,使用的增量越小(如研究人員所說,網格越細),模型的精度越高,數值求解所需的時間就越長。
神經網絡更擅長擬合這樣一個黑盒的未知函數,輸入是一個向量,而輸出是另一個向量。如果存在將一組輸入向量映射到一組輸出向量的函數,則可以訓練網絡以學習該映射,兩個有限維空間之間的任何函數都可以通過神經網絡近似。
2016年,研究人員研究了如何將通常用于圖像識別的深度神經網絡用于解決偏微分方程。首先,研究人員生成了用于訓練網絡的數據:一個數值求解器計算了流過xy且大小和方向不同的基本形狀(三角形,四邊形等)的簡單對象上流動的流體的速度場。2D圖像編碼有關對象幾何形狀和流體初始條件的信息作為輸入,而相應速度場的2D快照作為輸出。
從無限空間映射到無限空間
相比2016年的工作,這次的研究更有飛躍性的意義,該網絡不僅可以學習如何近似函數,還可以學習將函數映射到函數的「運算符」,而且沒有「維度爆炸」的困擾。例如,如果其他神經網絡或機器學習算法,希望錯誤率從10%下降到1%,則所需的訓練數據量或網絡規模可能會成倍爆炸,從而使任務無法實現。
在數學上,操作符的輸入輸出是沒有限制的,例如正弦函數sin(x),輸入和輸出端是無窮維的,因為x可以是任何值,函數可以是作用于x的任何變換。
學習近似算子的深度學習網絡可用于一次求解所有相似的偏微分方程,并針對一系列初始條件和邊界條件以及物理參數對相同現象進行建模。
1995年由工作表明,淺層網絡可以近似操作符算子。由于引入了神經網絡,所以此類算子稱為神經算子,即實際算子的近似值。
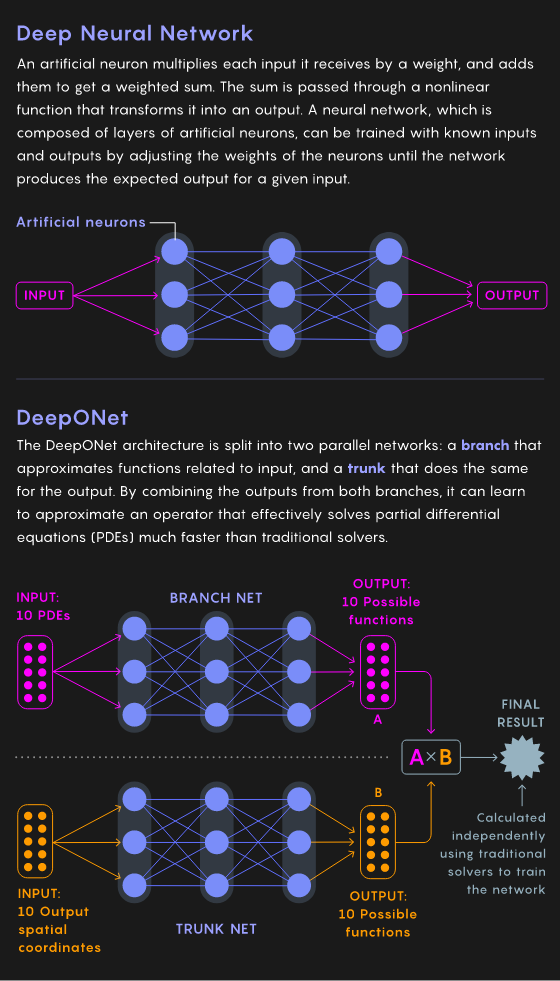
2019年,研究人員提出DeepONet,基于1995年的工作。它的的獨特之處在于它的分叉架構,該架構在兩個并行網絡(一個分支和一個主干)中處理數據。前者在輸入端學習一些函數的近似值,而后者在輸出端學習相同的函數。
DeepONet將兩個網絡的輸出合并,以了解偏微分方程所需的運算符。訓練DeepONet并在每次迭代中調整分支網絡和主干網絡中的權重,直到整個網絡幾乎沒有出現誤差允許范圍外的錯誤為止。
DeepONet一旦訓練后,就可以模擬操作符,可以在輸入端獲取代表偏微分方程的數據,其輸出為網絡訓練得到的近似解。
假設您提供了100個樣本,這些樣本代表了訓練數據中沒有的初始/邊界條件和物理參數,以及需要流場的位置,DeepONet可以在幾分之一秒內為您提供流場的狀態。
但,DeepONet的訓練過程仍然需要消耗大量算力,并且如何提升精確度,以及縮小步長產生更大的計算,也是一個問題。還能更快嗎?
改變觀點
去年,加州理工學院和普渡大學的Anandkumar及其同事建立了一個稱為傅立葉神經算子(FNO)的深度神經網絡,他們聲稱這種神經網絡具有更快的速度。
他們的網絡還將函數映射到函數,從無窮維空間到無窮維空間,并且他們在偏微分方程上測試了它們的神經網絡。
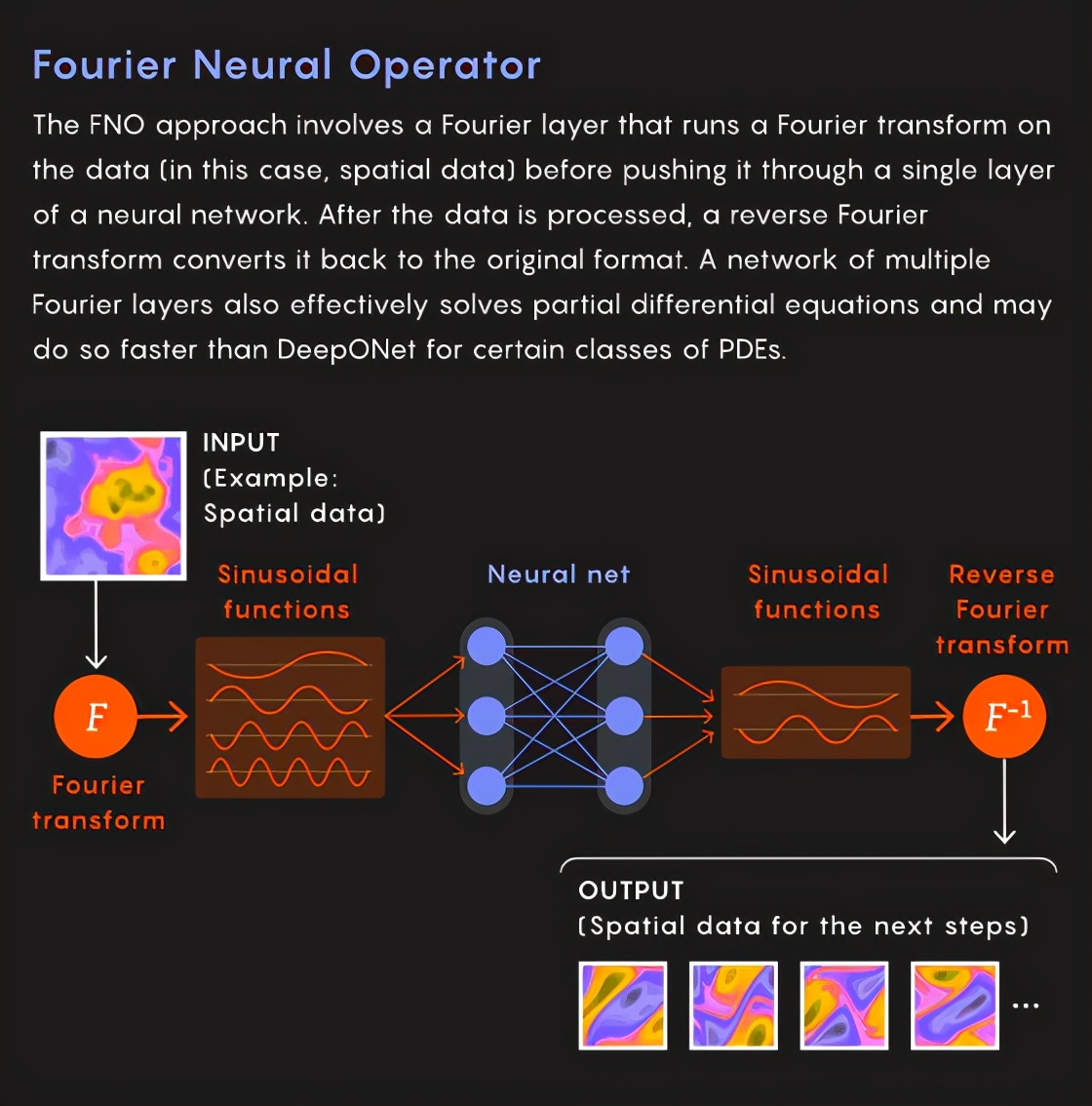
他們解決方案的核心是一個傅立葉層。
在他們將訓練數據推過神經網絡的單層之前,他們先對其進行了傅里葉變換。然后,當圖層通過線性運算處理了該數據時,他們將執行傅立葉逆變換,將其轉換回原始格式,此轉換是著名的傅里葉變換,它將連續函數分解為多個正弦函數。
整個神經網絡由幾個傅立葉層組成。
事實證明,此過程比DeepONet的計算更直接,并且類似于通過執行稱為PDE與某些其他函數之間的卷積的繁瑣數學運算來求解PDE。
在傅立葉域中,卷積涉及一個簡單的乘法,相當于將經過傅立葉變換的數據通過一層人工神經元(在訓練過程中獲得的精確權重),然后進行傅立葉逆變換。
因此,最終結果還是FNO學習了整個偏微分方程的操作符,將函數映射到函數。
這種方法顯著提升了求解速度。
在一個相對簡單的示例中,僅需要進行30,000次仿真,就能求出之前提到的Navier-Stokes方程的解,對于每個仿真,FNO花費了幾分之一秒的時間,而DeepONet為2.5秒。同樣的精度,傳統的求解器將花費18個小時。
數學意義
兩種團隊的方法都被證明是成功的,但是與廣泛使用神經網絡一樣,目前尚不清楚它們為什么如此出色以及是否在所有情況下都能如此。Mishra和他的同事現在正在對這兩種方法進行全面的數學理解。
經過一年的努力,在2月份,Mishra的團隊在Karniadakis的幫助下,對DeepONet架構進行了長達112頁的數學分析。他們證明了這種方法是真正通用的,因為它可以將輸入端的任何函數集映射到輸出端的任何函數集,而不僅僅是PDE,而不必為深入了解Karniadakis定理而做出某些假設網及其1995年的前身。
該團隊尚未完成分析FNO的論文,但是Mishra認為它可以比DeepONet更有效地解決某些特定問題。他的團隊正在對FNO進行詳細的分析,其中包括與DeepONet的比較。
但是,很明顯的是,這兩種方法都會超越傳統的求解器。對于一些無法寫出偏微分方程的場景中,神經算子可能是建模此類系統的唯一方法。
這是科學機器學習的未來。