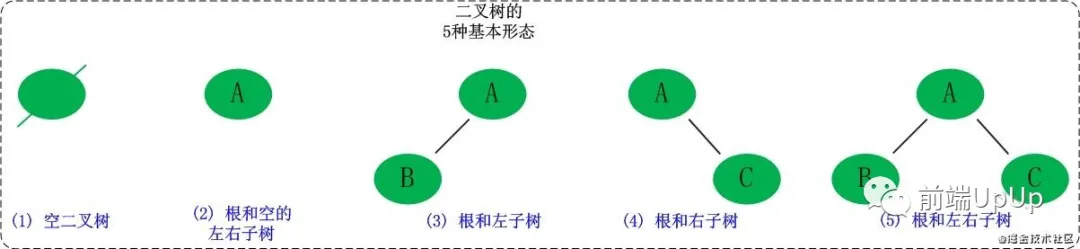
「算法與數據結構」二叉樹之美
前言
這次梳理的內容是數據結構專題中的「樹」,如果你看到樹這類數據結構時,滿腦子頭疼,覺得它很難理解,如果是這樣子的話,那么本文可能對你或許有點幫助。
俗話說得好,要想掌握理解的話,我們得先了解它的概念,性質等內容。
圍繞以下幾個點來展開介紹樹👇
樹的基本概念
- 基本術語
- 樹的種類
- 二叉樹概念
- 二叉樹的遍歷
- 二叉樹題目匯總
腦圖👇

樹的基本概念
樹是用來模擬具有樹狀結構性質的數據集合。或者你可以把它認為是一種「抽象數據結構」或是實現這種抽象數據類型的數據結構,用來模擬具有樹狀結構性質的數據集合。
那么根據維基百科給出的定義,我們似乎可以這么理解:
它是由n(n>0)個有限節點組成一個具有層次關系的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。它具有以下的特點:
- 每個節點都只有有限個子節點或無子節點;
- 沒有父節點的節點稱為根節點;
- 每一個非根節點有且只有一個父節點;
- 除了根節點外,每個子節點可以分為多個不相交的子樹;
- 樹里面沒有環路(cycle)
這個時候,我們就需要拿出一張圖來看👇
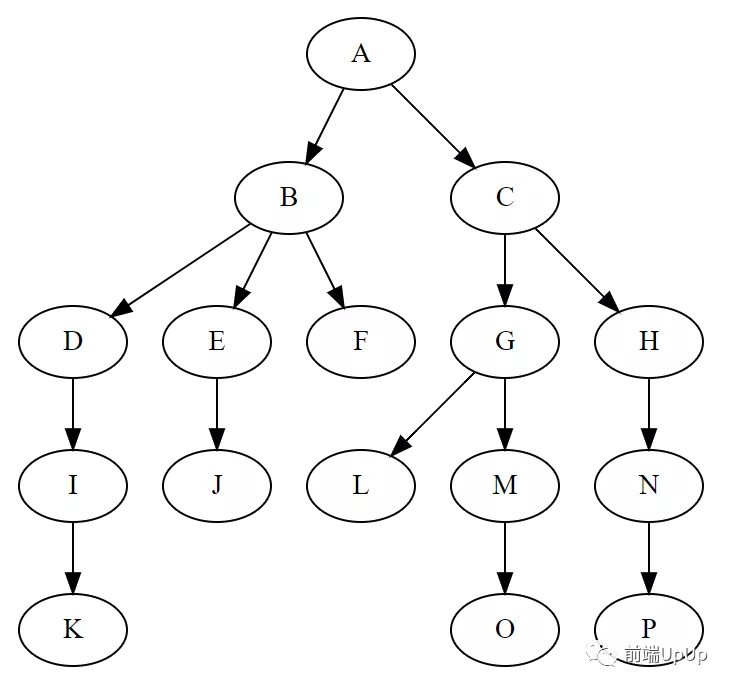
從圖中來看,以上的五個特點都可以很好的總結出來
- A節點作為根節點,沒有父節點,所以是根節點。
- 除根節點(A)外,其他的節點都有父節點,并且每個節點只有有限個子節點或無子節點。
- 從某個節點開始,可以分為很多個子樹,舉個例子,從B節點開始,即是如此。
既然對樹有一定認識后,我們需要了解它的一些術語。
基本術語
樹的基本術語
為了更加規范的總結,這里給出的描述來自于維基百科:
- 「節點的度」:一個節點含有的子樹的個數稱為該節點的度;
- 「樹的度」:一棵樹中,最大的節點度稱為樹的度;
- 「葉節點」或「終端節點」:度為零的節點;
- 「非終端節點」或「分支節點」:度不為零的節點;
- 「父親節點」或「父節點」:若一個節點含有子節點,則這個節點稱為其子節點的父節點;
- 「孩子節點」或「子節點」:一個節點含有的子樹的根節點稱為該節點的子節點;
- 「兄弟節點」:具有相同父節點的節點互稱為兄弟節點;
- 節點的「層次」:從根開始定義起,根為第1層,根的子節點為第2層,以此類推;
- 「深度」:對于任意節點n,n的深度為從根到n的唯一路徑長,根的深度為0;
- 「高度」:對于任意節點n,n的高度為從n到一片樹葉的最長路徑長,所有樹葉的高度為0;
- 「堂兄弟節點」:父節點在同一層的節點互為堂兄弟;
- 「節點的祖先」:從根到該節點所經分支上的所有節點;
- 「子孫」:以某節點為根的子樹中任一節點都稱為該節點的子孫;
- 「森林」:由m(m>=0)棵互不相交的樹的集合稱為森林。
可以結合上述的圖來理解這些概念,通過兩者的結合,你一定會對樹有進一步的了解的。
有以上基本概念,以及一些專業術語的掌握,接下來我們需要對樹進行一個分類,看看樹有哪些種類。
樹的種類
理解了樹的概念以及基本術語,接下來,我們需要拓展的內容就是樹的種類。
我們可以根據維基百科的依據來作為分類的標準👇
- 無序樹:樹中任意節點的子節點之間沒有順序關系,這種樹稱為無序樹,也稱為自由樹;
- 有序樹:樹中任意節點的子節點之間有順序關系,這種樹稱為有序樹;
- 完全二叉樹:對于一顆二叉樹,假設其深度為d(d>1)。除了第d層外,其它各層的節點數目均已達最大值,且第d層所有節點從左向右連續地緊密排列,這樣的二叉樹被稱為完全二叉樹;
- 平衡二叉樹(AVL樹):當且僅當任何節點的兩棵子樹的高度差不大于1的二叉樹;
- 排序二叉樹(英語:Binary Search Tree)):也稱二叉搜索樹、有序二叉樹;
- 滿二叉樹:所有葉節點都在最底層的完全二叉樹;
- 二叉樹:每個節點最多含有兩個子樹的樹稱為二叉樹;
- 霍夫曼樹:帶權路徑最短的二叉樹稱為哈夫曼樹或最優二叉樹;
- B樹:一種對讀寫操作進行優化的自平衡的二叉查找樹,能夠保持數據有序,擁有多于兩個子樹。
既然樹的分類有這么多的話,那么我們是不是都需要一一掌握呢,我個人覺得,掌握二叉樹這種結構就足夠了,它也是樹最簡單、應用最廣泛的種類。
那么接下來,我們就來介紹一下二叉樹吧。
二叉樹的概念
二叉樹是一種典型的樹樹狀結構。如它名字所描述的那樣,二叉樹是每個節點最多有兩個子樹的樹結構,通常子樹被稱作“左子樹”和“右子樹”。
二叉樹
從這個圖片的內容來看,應該很清楚的展示了二叉樹的結構。
至于二叉樹的性質的話,可以參考下圖,作為補充知識吧,個人覺得這個不是重點。
二叉樹的性質
重點的話,我們需要掌握的應該是它的遍歷方式。
二叉樹的遍歷
我們知道對于二叉樹的遍歷而言,有常見得三種遍歷方式,分別是以下三種:
- 前序遍歷
- 中序遍歷
- 后續遍歷
對于任何一種遍歷方式而言,我們不僅需要掌握它的非遞歸版本,同時對于它的遞歸版本來說,更是考察一個人的算法基本功,那么接下來,我們來看看吧。
前序遍歷
點擊這里,練習二叉樹的前序遍歷
給你二叉樹的根節點 root ,返回它節點值的 「前序」 遍歷。
假設我們mock一下假數據👇
- 輸入: [1,null,2,3]
- 1
- \
- 2
- /
- 3
- 輸出: [1,3,2]
那么根據我們對前序遍歷的理解,我們可以寫出解題偽代碼👇
- // TianTianUp
- // * function TreeNode(val, left, right) {
- // * this.val = (val===undefined ? 0 : val)
- // * this.left = (left===undefined ? null : left)
- // * this.right = (right===undefined ? null : right)
- // * }
- let inorderTraversal = (root, arr = []) => {
- if(root) {
- inorderTraversal(root.left, arr)
- arr.push(root.value)
- inorderTraversal(root.right, arr)
- }
- return arr
- }
非遞歸版本👇
對于非遞歸的話,我們需要借助一個數據結構去存儲它的節點,需要使用的就是棧,它的思路可以借鑒👇
- 根節點為目標節點,開始向它子節點遍歷
- 1.訪問目標節點
- 2.左孩子入棧 -> 直至左孩子為空的節點
- 3.節點出棧,以右孩子為目標節點,再依次執行1、2、3
- let preorderTraversal = (root, arr = []) => {
- const stack = [], res = []
- let current = root
- while(current || stack.length > 0) {
- while (current) {
- res.push(current.val)
- stack.push(current)
- current = current.left
- }
- current = stack.pop()
- current = current.right
- }
- return res
- }
中序遍歷
給定一個二叉樹,返回它的中序 遍歷。
示例:
- 輸入: [1,null,2,3] 1
- 2 / 3
- 輸出: [1,3,2]
進階: 遞歸算法很簡單,你可以通過迭代算法完成嗎?
遞歸版本👇
- const inorderTraversal = (root, arr = []) => {
- if(root) {
- inorderTraversal(root.left, arr)
- arr.push(root.val)
- inorderTraversal(root.right, arr)
- }
- return arr
- }
非遞歸版本,這里就不解釋了,跟前序遍歷一樣,思路一樣,用棧維護節點信息。
- const inorderTraversal = (root, arr = []) => {
- const stack = [], res = []
- let current = root
- while(current || stack.length > 0) {
- while (current) {
- stack.push(current)
- current = current.left
- }
- current = stack.pop()
- res.push(current.val)
- current = current.right
- }
- return res
- }
后續遍歷
給定一個二叉樹,返回它的 后序 遍歷。
示例:
- 輸入: [1,null,2,3]
- 1
- 2 / 3
- 輸出: [3,2,1]
進階: 遞歸算法很簡單,你可以通過迭代算法完成嗎?
來源:力扣(LeetCode) 鏈接:https://leetcode-cn.com/problems/binary-tree-postorder-traversal 著作權歸領扣網絡所有。商業轉載請聯系官方授權,非商業轉載請注明出處。
遞歸版本👇
- const postorderTraversal = (root, arr = []) => {
- if(root) {
- postorderTraversal(root.left, arr)
- postorderTraversal(root.right, arr)
- arr.push(root.val)
- }
- return arr
- }
非遞歸版本👇
其實,嗯,做完前面兩個后,會發現都是有套路滴~
- const postorderTraversal = (root, arr = []) => {
- const stack = [], res = []
- let current = root, last = null // last指針記錄上一個節點
- while(current || stack.length > 0) {
- while (current) {
- stack.push(current)
- current = current.left
- }
- current = stack[stack.length - 1]
- if (!current.right || current.right == last) {
- current = stack.pop()
- res.push(current.val)
- last = current
- current = null // 繼續彈棧
- } else {
- current = current.right
- }
- }
- return res
- }
二叉樹的層次遍歷 ⭐⭐
鏈接:二叉樹的層序遍歷
給你一個二叉樹,請你返回其按 「層序遍歷」 得到的節點值。(即逐層地,從左到右訪問所有節點)。
示例:二叉樹:[3,9,20,null,null,15,7],
- 3
- /
- 9 20 /
- 15 7
返回其層次遍歷結果:
- [ [3], [9,20], [15,7] ]
來源:力扣(LeetCode) 鏈接:https://leetcode-cn.com/problems/binary-tree-level-order-traversal 著作權歸領扣網絡所有。商業轉載請聯系官方授權,非商業轉載請注明出處。
遞歸版本👇
- const levelOrder = function(root) {
- if(!root) return []
- let res = []
- dfs(root, 0, res)
- return res
- }
- function dfs(root, step, res){
- if(root){
- if(!res[step]) res[step] = []
- res[step].push(root.val)
- dfs(root.left, step + 1, res)
- dfs(root.right, step + 1, res)
- }
- }
非遞歸版本👇
這里借助的就是隊列這個數據結構,先進先出的機制。
- const levelOrder = (root) => {
- let queue = [], res = []
- if (root) queue.push(root);
- while (queue.length) {
- let next_queue = [],
- now_res = []
- while (queue.length) {
- root = queue.shift()
- now_res.push(root.val)
- root.left && next_queue.push(root.left)
- root.right && next_queue.push(root.right)
- }
- queue = next_queue
- res.push(now_res)
- }
- return res
- }
題目匯總
還是那句話,題目做不完的,剩下的就靠刷leetcode了,我還準備了一些常見的二叉樹題集,題目的質量還是不錯的👇
- 二叉樹的最小深度⭐
- 二叉樹的最大深度⭐
- 相同的樹⭐
- 二叉搜索樹的范圍和⭐
- 對稱二叉樹⭐
- 將有序數組轉換為二叉搜索樹⭐
- 二叉樹的層次遍歷 II⭐⭐
- 二叉樹的最近公共祖先⭐⭐
- 驗證二叉搜索樹⭐⭐
- 路徑總和 III⭐⭐
- 存在重復元素 III⭐⭐
- 計算右側小于當前元素的個數⭐⭐⭐