二叉樹的定義以及存儲結構
二叉樹的定義:
二叉樹是n個結點的有限集合,該集合或者為空集,或者由一個根結點和兩顆互不相交的、分別稱為根結點的左子樹和右子樹的二叉樹組成。
二叉樹具有五種基本的形態:
- 空二叉樹。
- 只有一個根結點。
- 根結點只有左子樹。
- 根結點只有右子樹。
特殊的二叉樹
- 斜樹。
- 滿二叉樹。
- 完全二叉樹。
二叉樹的順序存儲結構:
二叉樹的順序存儲結構就是用一維數組存儲二叉樹中的結點,并且結點的存儲位置,也就是數組的下標要能體現結點之間的邏輯關系,比如雙親與孩子的關系,左右兄弟的關系。
使用順序存儲結構表現二叉樹的時候,在其線性結構中,會存在一些空結點,但是其會占據一定的內存空間,會造成存儲空間的浪費;所以,順序存儲結構一般只用于完全二叉樹。
二叉樹的鏈式存儲結構:
由于二叉樹的每個結點最多有兩個孩子,所以為每個結點設計一個數據域和兩個指針域,通常將其稱之為二叉鏈表。
二叉鏈表的結點結構定義代碼:
- typedef char TElemType;
- typedef struct BinaryTreeNode{
- TElemType data;
- //lchild指向左結點的指針
- //rchild指向右結點的指針
- struct BinaryTreeNode *lchild,*rchild;
- }BinaryTreeNode,*BinaryTree;
二叉樹的遍歷
二叉樹的遍歷是指從根結點出發,按照某種次序一次訪問二叉樹中所有結點,使得每個結點被訪問一次且僅被訪問一次。
二叉樹的遍歷方法:
- 前序遍歷
- 中序遍歷
- 后序遍歷
1.首先創建一棵二叉樹
構建二叉樹,向結點的數據域中添加字符。
- void CreateBinaryTree(BinaryTree *T){
- TElemType ch;
- cin>>ch;
- if (ch=='$'){
- *T=NULL;
- }else{
- *T=new BinaryTreeNode;
- if (!*T)return;
- (*T)->data=ch;
- CreateBinaryTree(&(*T)->lchild);
- CreateBinaryTree(&(*T)->rchild);
- }
- }
2.二叉樹的前序遍歷算法
- void PreOrderTraverse(BinaryTree T){
- if (T==NULL){
- cout<<"#"<<" ";
- return;
- }
- cout<<T->data<<" ";
- PreOrderTraverse(T->lchild);
- PreOrderTraverse(T->rchild);
- }
3.二叉樹的中序遍歷算法
- void InOderTraverse(BinaryTree T){
- if(T!=NULL){
- cout<<"#"<<" ";
- return;
- }
- InOderTraverse(T->lchild);
- cout<<T->data<<" ";
- InOrderTraverse(T->rchild);
- }
4.二叉樹的后序遍歷算法
- void PostOrderTraverse(BinaryTree T){
- if (T->NULL){
- cout<<"#"<<" ";
- return;
- }
- PostOrderTraverse(T->lchild);
- PostOrderTraverse(T->rchild);
- cout<<T->data<<" ";
- }
前序遍歷、中序遍歷和后序遍歷算法的核心算法大致相同,都是利用了函數遞歸的原理。這里順帶補充一下關于函數遞歸調用的原理:
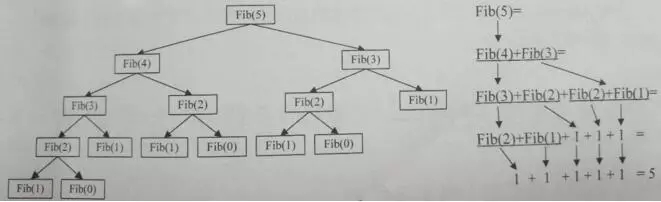
裴波那契數列的實現來講解函數的遞歸調用,假設存在這樣一個函數:
使用遞歸實現裴波那契數列代碼如下:
- int Fibonacci(int i){
- if (i<2){
- return i==0?0:1;
- }
- return Fibonacci(i-1)+Fibonacci(i-2);
- }
通過二叉樹的結構來分析遞歸調用的執行過程:(摘自大話數據結構 P103頁)
主函數中的測試代碼如下:
- //測試代碼int main()
- {
- BinaryTree tree = new BinaryTreeNode;
- cout << "構建一顆由字符構成的二叉樹,#代表空" << endl;
- CreateBinaryTree(&tree);
- cout << "二叉樹的前序遍歷輸出" << endl;
- PreOderTraverse(tree);
- cout << endl;
- cout << "二叉樹的中序遍歷輸出" << endl;
- InOderTraverse(tree);
- cout << endl;
- cout << "二叉樹的后序遍歷輸出" << endl;
- PostOderTraverse(tree);
- cout << endl;
- return 0;
- }
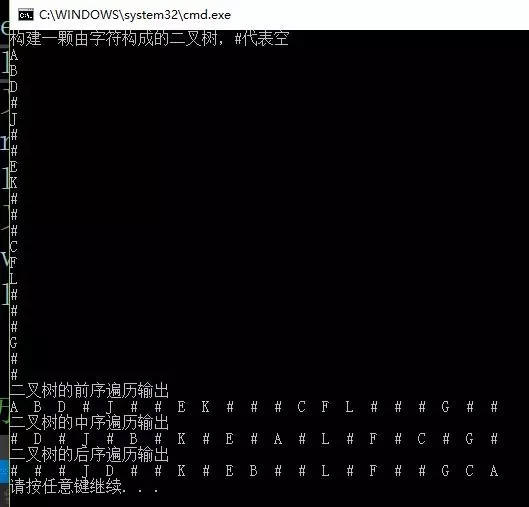
輸出如下圖所示:
假設輸入這樣一個二叉樹數據結構:
代表當前節點的數據域為空
ABD#J##EK###CFL###G##