Java編程內功-數據結構與算法「平衡二叉樹」

作者：Java精髓 2021-04-01 10:34:18

開發后端算法

本篇繼續給大家介紹關于Java編程的相關知識，今天主要介紹數據結構與算法之平衡二叉樹，希望對你有所幫助！

[[390860]]

二叉排序樹可能的問題

給定一個數列{1,2,3,4,5,6}，要求創建一個二叉排序樹(BST)，分析問題所在

問題分析：

左子樹全部為空，從形式上看，更像一個單鏈表;
插入速度沒有影響;
查詢速度明顯降低(因為需要一次比較)，不能發揮BST的優勢。因為每次還要比較左子樹，其查詢速度，比單鏈表還慢。
解決方案-平衡二叉樹(ALV)

基本介紹

平衡二叉樹也叫平衡二叉搜索樹(Self-balancing binary search tree)，又稱為AVL樹，可以保證查詢效率較高。
具有以下特點：它是一顆空樹或它的左右兩個子樹的高度差的絕對值不超過1，并且左右兩個子樹都是一顆平衡二叉樹。平衡二叉樹的常用實現方法有紅黑樹、AVL、替罪羊樹、Treap、伸展樹等;
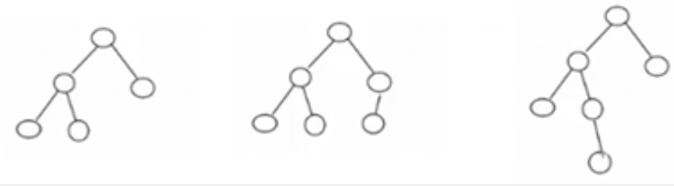
舉例說明，下圖前兩個都是平衡二叉樹，第一個左右子樹的高度差絕對值是1，第二個左右子樹高度差的絕對值是0，而第三個的左右子樹高度差的絕對值是2，這樣第三個就不是平衡二叉樹;

平衡二叉樹之左旋轉

步驟：

創建一個新的節點newNode，值等于當前根節點的值。
把新節點的左子樹設置成當前節點的左子樹。
把新節點的右子樹設置成當前節點的右子樹的左子樹。
把當前節點的值換為當前右子節點的值。
把當前節點的右子樹設置成右子樹的右子樹。
把當前節點的左子樹設置為新的節點。

平衡二叉樹之右旋轉

步驟：

創建一個新的節點，值等于當前根的節點的值。
把新節點的右子樹設置成當前節點的右子樹。
把新節點的左子樹設置成當前節點的左子樹的右子樹。
把當前節點的值換位左子節點的值。
把當前節點的左子樹設置成左子樹的左子樹。
把當前節點的右子樹設置為新的節點。

平衡二叉樹之雙旋轉

在某些情況下，單旋轉不能完成完成平衡二叉樹的轉換，需要進行兩次旋轉。

如果它的右子樹的左子樹的高度大于它的右子樹的右子樹的高度，需要先對右子樹進行右旋轉，再對當前節點進行左旋轉。
如果它的左子樹的右子樹高度大于它的左子樹的左子樹高度，
需要對左子樹先進行左旋轉,再對當前節點進行右旋轉。

代碼案例

package com.xie.avl; 
 
public class AVLTreeDemo { 
    public static void main(String[] args) { 
        int[] arr = {4, 3, 6, 5, 7, 8}; 
        AVLTree avlTree = new AVLTree(); 
        for (int i = 0; i < arr.length; i++) { 
            avlTree.add(new Node(arr[i])); 
        } 
        System.out.println("中序遍歷"); 
        avlTree.infixOrder(); 
        System.out.println("在沒有平衡處理前~~"); 
        System.out.println("樹的高度=" + avlTree.getRoot().height()); 
        System.out.println("樹的左子樹的高度=" + avlTree.getRoot().leftHeight()); 
        System.out.println("樹的右子樹的高度=" + avlTree.getRoot().rightHeight()); 
    } 
} 
 
class AVLTree { 
    private Node root; 
 
    public Node getRoot() { 
        return root; 
    } 
 
    public void setRoot(Node root) { 
        this.root = root; 
    } 
 
    //查找要刪除的節點的父節點 
    public Node searchParent(Node node) { 
        if (root != null) { 
            return root.searchParent(node); 
        } else { 
            return null; 
        } 
    } 
 
    //查找要刪除的節點 
    public Node search(int value) { 
        if (root == null) { 
            return null; 
        } else { 
            return root.search(value); 
        } 
    } 
 
    /** 
     * 找到以node 根的二叉排序樹的最小值，并刪除以node 為根節點的二叉排序樹的最小節點 
     * 
     * @param node 傳入節點（當做二叉排序樹的根節點) 
     * @return 返回以node為根節點的二叉排序樹的最小節點值 
     */ 
    public int delRightTreeMin(Node node) { 
        Node target = node; 
        //循環查找左節點 
        while (target.left != null) { 
            target = target.left; 
        } 
        //刪除最小節點 
        delNode(target.value); 
        return target.value; 
    } 
 
    /** 
     * 找到以node 根的二叉排序樹的最大值，并刪除以node 為根節點的二叉排序樹的最大節點 
     * 
     * @param node 傳入節點（當做二叉排序樹的根節點) 
     * @return 返回以node為根節點的二叉排序樹的最大節點值 
     */ 
    public int delLeftTreeMax(Node node) { 
        Node target = node; 
        while (target.right != null) { 
            target = target.right; 
        } 
 
        //刪除最大節點 
        delNode(target.value); 
        return target.value; 
    } 
 
    //刪除節點 
    public void delNode(int value) { 
        if (root == null) { 
            return; 
        } else { 
            Node targetNode = search(value); 
            if (targetNode == null) { 
                return; 
            } 
            if (targetNode == root) { 
                root = null; 
                return; 
            } 
            Node parentNode = searchParent(targetNode); 
 
            if (targetNode.left == null && targetNode.right == null) { 
                //如果要刪除的節點是葉子節點 
                if (parentNode.left != null && parentNode.left.value == targetNode.value) { 
                    parentNode.left = null; 
                } 
                if (parentNode.right != null && parentNode.right.value == targetNode.value) { 
                    parentNode.right = null; 
                } 
            } else if (targetNode.left != null && targetNode.right != null) { 
                //如果要刪除的節點是有兩個子樹的節點 
                int minValue = delRightTreeMin(targetNode.right); 
                targetNode.value = minValue; 
                //上下代碼刪除效果一樣 
                //int maxValue = delLeftTreeMax(targetNode.left); 
                //targetNode.value = maxValue; 
            } else { 
                //要刪除的節點是只有左子節點 
                if (targetNode.left != null) { 
                    if (parentNode != null) { 
                        if (parentNode.left == targetNode) { 
                            parentNode.left = targetNode.left; 
                        } else { 
                            parentNode.right = targetNode.left; 
                        } 
                    } else { 
                        //如果父節點是空，讓root換位 
                        root = targetNode.left; 
                    } 
                } else {//要刪除的節點是只有右子節點 
                    if (parentNode != null) { 
                        if (parentNode.left == targetNode) { 
                            parentNode.left = targetNode.right; 
                        } else { 
                            parentNode.right = targetNode.right; 
                        } 
                    } else { 
                        //如果父節點是空，讓root換位 
                        root = targetNode.right; 
                    } 
 
                } 
            } 
        } 
    } 
 
    //添加節點 
    public void add(Node node) { 
        if (root == null) { 
            root = node; 
        } else { 
            root.add(node); 
        } 
    } 
 
    //中序遍歷 
    public void infixOrder() { 
        if (root != null) { 
            root.infixOrder(); 
        } else { 
            System.out.println("二叉排序為空，不能遍歷"); 
        } 
    } 
} 
 
class Node { 
    int value; 
    Node left; 
    Node right; 
 
    public Node(int value) { 
        this.value = value; 
    } 
 
    /** 
     * 返回左子樹的高度 
     * 
     * @return 
     */ 
    public int leftHeight() { 
        if (left == null) { 
            return 0; 
        } 
        return left.height(); 
    } 
 
    /** 
     * 返回右子樹的高度 
     * 
     * @return 
     */ 
    public int rightHeight() { 
        if (this.right == null) { 
            return 0; 
        } 
        return right.height(); 
    } 
 
    /** 
     * 返回以該節點為根節點的樹的高度 
     * 
     * @return 
     */ 
    public int height() { 
        return Math.max(this.left == null ? 0 : this.left.height(), this.right == null ? 0 : this.right.height()) + 1; 
    } 
 
    /** 
     * 左旋轉 
     */ 
    public void leftRotate() { 
        //創建新的節點，以當前根節點的值 
        Node newNode = new Node(value); 
        //把新的節點的左子樹設置為當前節點的左子樹 
        newNode.left = left; 
        //把新的右子樹設置為當前節點的右子樹的左子樹 
        newNode.right = right.left; 
        //把當前節點的值替換成右子節點的值 
        value = right.value; 
        //把當前節點的右子樹設置成當前節點的右子節點的右子樹 
        right = right.right; 
        //把當前的節點的左子節點(左子樹),設置成新的節點 
        left = newNode; 
    } 
 
    /** 
     * 右旋轉 
     */ 
    public void rightRotate() { 
        //創建新的節點，以當前根節點的值 
        Node newNode = new Node(value); 
        //把新的節點的右子樹設置成當前節點的右子樹 
        newNode.right = right; 
        //把新的節點的左子樹設置為當前節點左子樹的右子樹 
        newNode.left = left.right; 
        //把當前節點的值換為左子節點的值 
        value = left.value; 
        //把當前節點左子樹設置成左子樹的左子樹 
        left = left.left; 
        //把當前節點的右子樹設置新節點 
        right = newNode; 
    } 
 
    /** 
     * 查找要刪除節點的父節點 
     * 
     * @param node 要刪除的節點 
     * @return 要刪除節點的父節點 
     */ 
    public Node searchParent(Node node) { 
        //如果當前節點就是要刪除節點的父節點就返回 
        if ((this.left != null && this.left.value == node.value) || 
                (this.right != null && this.right.value == node.value)) { 
            return this; 
        } else { 
            if (this.left != null && node.value < this.value) { 
                //如果查找的節點的值小于當前節點的值，向左子樹遞歸查找 
                return this.left.searchParent(node); 
            } else if (this.right != null && value >= this.value) { 
                //如果查找的節點的值小于當前節點的值，向左子樹遞歸查找 
                return this.right.searchParent(node); 
            } else { 
                return null; 
            } 
        } 
    } 
 
    /** 
     * 查找要刪除的節點 
     * 
     * @param value 要刪除的節點的值 
     * @return 刪除的節點 
     */ 
    public Node search(int value) { 
        if (value == this.value) { 
            return this; 
        } else if (value < this.value) { 
            if (this.left != null) { 
                return this.left.search(value); 
            } else { 
                return null; 
            } 
        } else { 
            if (this.right != null) { 
                return this.right.search(value); 
            } else { 
                return null; 
            } 
        } 
    } 
 
    //遞歸的形式添加節點，滿足二叉排序樹的要求 
    public void add(Node node) { 
        if (node == null) { 
            return; 
        } 
        if (node.value < this.value) { 
            if (this.left == null) { 
                this.left = node; 
            } else { 
                //遞歸向左子樹添加 
                this.left.add(node); 
            } 
        } else { 
            if (this.right == null) { 
                this.right = node; 
            } else { 
                //遞歸向右子節點添加 
                this.right.add(node); 
            } 
        } 
 
        //當添加完一個節點后，如果（右子樹高度-左子樹高度）> 1 ，進行左旋轉 
        if (rightHeight() - leftHeight() > 1) { 
            //如果它的右子樹的左子樹的高度大于它的右子樹的右子樹的高度，需要先對右子樹進行右旋轉，再對當前節點進行左旋轉 
            if(right != null && right.leftHeight()>right.rightHeight()){ 
                right.rightRotate(); 
                leftRotate(); 
            }else{ 
                //直接進行左旋轉即可 
                leftRotate(); 
            } 
            return; 
        } 
 
        //當添加完一個節點后，如果（左子樹高度-右子樹高度）> 1 ，進行右旋轉 
        if (leftHeight() - rightHeight() > 1) { 
            //如果它的左子樹的右子樹高度大于它的左子樹的左子樹高度，需要對左子樹先進行左旋轉,再對當前節點進行右旋轉 
            if(left != null && left.rightHeight() > left.leftHeight()){ 
                left.leftRotate(); 
                rightRotate(); 
            }else{ 
                //直接進行右旋轉即可 
                rightRotate(); 
            } 
 
        } 
    } 
 
    //中序遍歷 
    public void infixOrder() { 
        if (this.left != null) { 
            this.left.infixOrder(); 
        } 
        System.out.println(this); 
        if (this.right != null) { 
            this.right.infixOrder(); 
        } 
    } 
 
    @Override 
    public String toString() { 
        return "Node{" + 
                "value=" + value + 
                '}'; 
    } 
}

【編輯推薦】

微服務面試必問的Dubbo，這么詳細還怕自己找不到工作？
2021年值得關注的5個IT行業發展趨勢
免費的安全軟件落寞！讓人唏噓
界面UI即將大改！Windows1021H2最新預覽版搶先看
微軟為 Windows101909 推送 KB5000850 更新，修復資源管理器搜索等問題

責任編輯：姜華來源：今日頭條

Java編程數據結構算法

成人免费xxxxx在线视频软件_久久精品久久久_亚洲国产精品久久久_天天色天天色_亚洲人成一区_欧美一级欧美三级在线观看

Java編程內功-數據結構與算法「平衡二叉樹」

二叉排序樹可能的問題

基本介紹

平衡二叉樹之左旋轉

平衡二叉樹之右旋轉

平衡二叉樹之雙旋轉

代碼案例