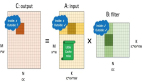
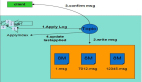
感知器及其在Python中的實現
什么是感知器?
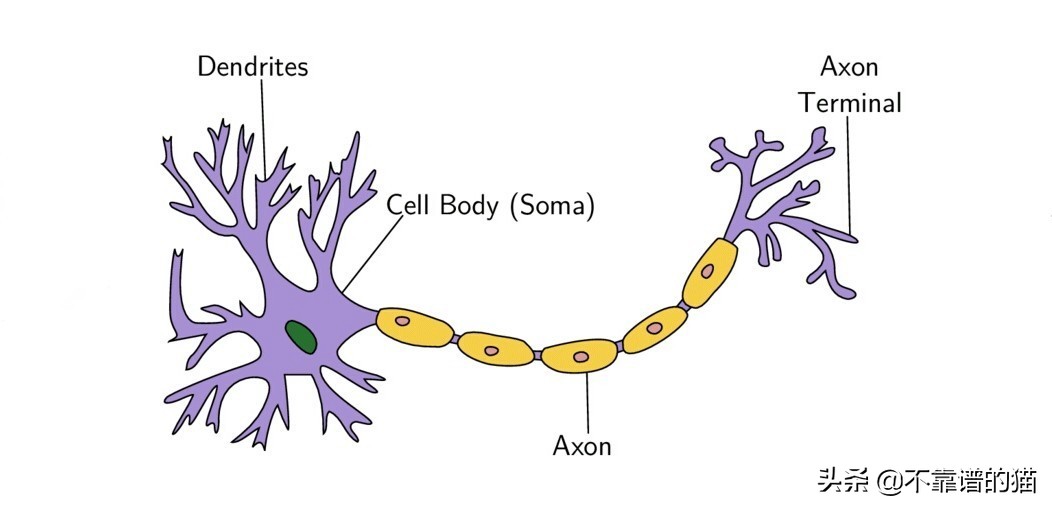
生物神經元示意圖
感知器的概念類似于大腦基本處理單元神經元的工作原理。神經元由許多由樹突攜帶的輸入信號、胞體和軸突攜帶的一個輸出信號組成。當細胞達到特定閾值時,神經元會發出一個動作信號。這個動作要么發生,要么不發生。
類似地,感知器具有許多輸入(通常稱為特征),這些輸入被饋送到產生一個二元輸出的線性單元中。因此,感知器可用于解決二元分類問題,其中樣本將被識別為屬于預定義的兩個類之一。
算法

感知器原理圖
由于感知器是二元類器(0/1),我們可以將它們的計算定義如下:
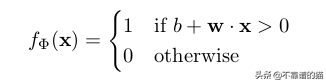
讓我們回想一下,兩個長度為n的向量的點積由下式給出:
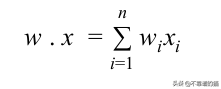
函數f(x)= b + w.x是權重和特征向量的線性組合。 因此,感知器是線性分類器-一種使用線性預測器函數進行預測的算法。
權重表示x中每個特征xᵢ 對機器學習模型行為的有效性。特征xᵢ的權重wᵢ越高,對輸出的影響就越大。偏差“ b”類似于線性方程式中的截距,它是一個常數,可以幫助機器學習模型以最適合數據的方式進行調整。偏差項假設虛擬輸入特征系數x₀= 1。
可以使用以下算法訓練模型:

Python實現
我們考慮用于實現感知器的機器學習數據集是鳶尾花數據集。這個數據集包含描述花的4個特征,并將它們歸類為屬于3個類中的一個。我們剝離了屬于類' Iris-virginica '的數據集的最后50行,只使用了兩個類' Iris-setosa '和' Iris-versicolor ',因為這些類是線性可分的,算法通過最終找到最優權重來收斂到局部最小值。
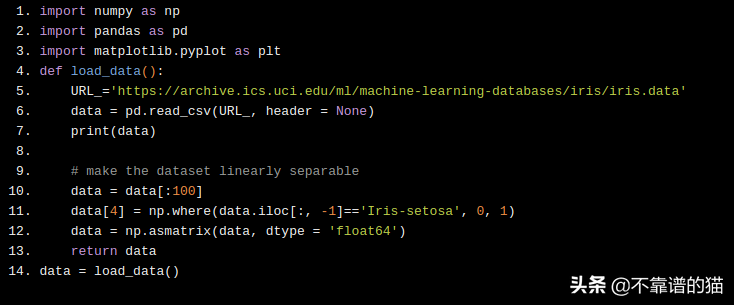
- import numpy as np
- import pandas as pd
- import matplotlib.pyplot as plt
- def load_data():
- URL_='https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
- data = pd.read_csv(URL_, header = None)
- print(data)
- # make the dataset linearly separable
- data = data[:100]
- data[4] = np.where(data.iloc[:, -1]=='Iris-setosa', 0, 1)
- data = np.asmatrix(data, dtype = 'float64')
- return data
- data = load_data()
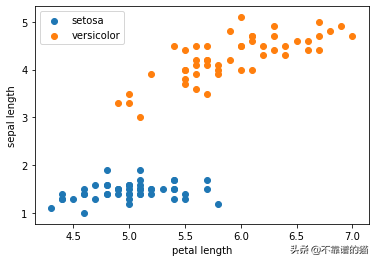
將具有兩個特征的數據集可視化,我們可以看到,通過在它們之間畫一條直線,可以清楚地分隔數據集。
我們的目標是編寫一個算法來找到這條線并正確地對所有這些數據點進行分類。
- plt.scatter(np.array(data[:50,0]), np.array(data[:50,2]), marker='o', label='setosa')
- plt.scatter(np.array(data[50:,0]), np.array(data[50:,2]), marker='x', label='versicolor')
- plt.xlabel('petal length')
- plt.ylabel('sepal length')
- plt.legend()
- plt.show()

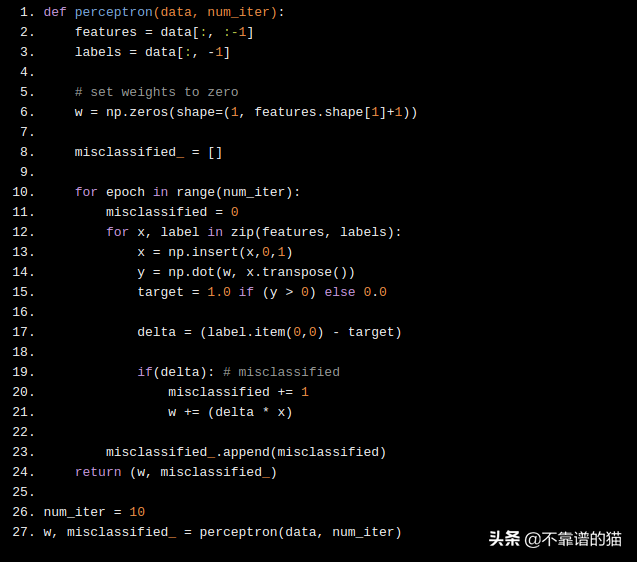
現在我們實現上面提到的算法,看看它是如何工作的。我們有4個特征,因此每個特征有4個權重。請記住,我們定義了一個偏置項w₀,假設x₀= 1,使其總共具有5個權重。
我們將迭代次數定義為10。這是超參數之一。在每次迭代時,算法都會為所有數據點計算類別(0或1),并隨著每次錯誤分類更新權重。
如果樣本分類錯誤,則權值將由向相反方向移動的增量更新。因此,如果再次對樣本進行分類,結果就會“錯誤較少”。我們將任何label≤0歸類為“0”(Iris-setosa),其它歸類為“1”(Iris-versicolor)。
- def perceptron(data, num_iter):
- features = data[:, :-1]
- labels = data[:, -1]
- # set weights to zero
- w = np.zeros(shape=(1, features.shape[1]+1))
- misclassified_ = []
- for epoch in range(num_iter):
- misclassified = 0
- for x, label in zip(features, labels):
- x = np.insert(x,0,1)
- y = np.dot(w, x.transpose())
- target = 1.0 if (y > 0) else 0.0
- delta = (label.item(0,0) - target)
- if(delta): # misclassified
- misclassified += 1
- w += (delta * x)
- misclassified_.append(misclassified)
- return (w, misclassified_)
- num_iter = 10
- w, misclassified_ = perceptron(data, num_iter)
現在,讓我們繪制每次迭代中分類錯誤的樣本數。我們可以看到該算法在第4次迭代中收斂。也就是說,所有樣本在第4次通過數據時都已正確分類。
感知器的一個特性是,如果數據集是線性可分離的,那么該算法一定會收斂!
- epochs = np.arange(1, num_iter+1)
- plt.plot(epochs, misclassified_)
- plt.xlabel('iterations')
- plt.ylabel('misclassified')
- plt.show()

局限性
- 僅當數據集可線性分離時,單層感知器才有效。
- 該算法僅用于二元分類問題。但是,我們可以通過在每個類中引入一個感知器來擴展算法以解決多類分類問題。