免費Python機器學習課程二:多元線性回歸
從頭開始學習為Python中任意數量的變量開發多元線性回歸。
線性回歸可能是最簡單的機器學習算法。對于初學者來說非常好,因為它使用簡單的公式。因此,這對學習機器學習概念很有幫助。在本文中,我將嘗試逐步解釋多元線性回歸。
概念和公式
線性回歸使用我們在學校都學過的簡單公式:
Y = C + AX
提醒一下,Y是輸出或因變量,X是輸入或自變量,A是斜率,C是截距。
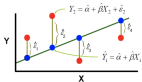
對于線性回歸,對于相同的公式,我們遵循以下符號:
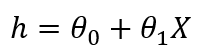
如果我們有多個自變量,則線性回歸的公式將如下所示:
在這里," h"稱為假設。這是預測的輸出變量。Theta0是偏差項,所有其他theta值是系數。它們首先是隨機啟動的,然后使用算法進行優化,以便此公式可以緊密預測因變量。
成本函數和梯度下降
當theta值從一開始就被初始化時,該公式未經過訓練以預測因變量。該假設與原始輸出變量" Y"相去甚遠。這是估算所有訓練數據的累積距離的公式:
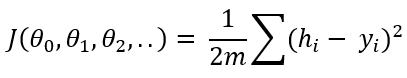
這稱為成本函數。如果您注意到了,它從假設(預測輸出)中減去y(原始輸出),取平方去掉負數,求和除以2乘以m。在此,m是訓練數據的數量。您可能會看到成本函數是原始輸出和預測輸出之間差異的指示。機器學習算法的思想是最小化成本函數,以使原始輸出與預測輸出之間的差異更小。為此,我們需要優化theta值。
這是我們更新theta值的方法。我們將成本函數相對于每個theta值的偏微分,然后從現有theta值中減去該值,
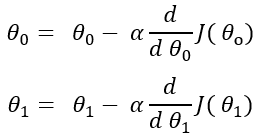
在此,alpha是學習率,它是一個常數。我沒有為所有theta值顯示相同的公式。但這是所有theta值的相同公式。經過微分后,公式得出為:
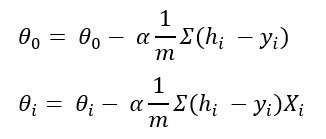
這稱為梯度下降。
逐步實現算法
我要使用的數據集來自吳安德(Andre Ng)的Coursera機器學習課程。我將在此頁面底部提供鏈接。請隨時下載數據集并通過本教程進行練習。我鼓勵您在閱讀數據集時進行練習(如果這對您來說是新的)。那是了解它的唯一方法。
在此數據集中,只有兩個變量。但是我開發了適用于任意數量變量的算法。如果您對10個變量或20個變量使用相同的算法,那么它也應該工作。我將在Python中使用Numpy和Pandas庫。所有這些豐富的Python庫使機器學習算法更加容易。導入包和數據集:
- import pandas as pd
- import numpy as np
- df = pd.read_csv('ex1data2.txt', header = None)
- df.head()
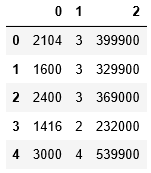
(1) 在偏項中添加一列。之所以選擇1,是因為如果您將一個值乘以任意值,則該值不會改變。
- df = pd.concat([pd.Series(1, index=df.index, name='00'), df], axis=1)
- df.head()
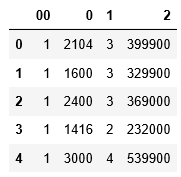
(2) 定義輸入變量或自變量X以及輸出變量或因變量y。在此數據集中,列0和1是輸入變量,列2是輸出變量。
- X = df.drop(columns=2)
- y = df.iloc[:, 3]
(3) 通過將每一列除以該列的最大值來標準化輸入變量。這樣,每列的值將在0到1之間。此步驟不是必需的。但這會使算法更快地達到最佳狀態。同樣,如果您注意到數據集,則列0的元素與列1的元素相比太大。如果對數據集進行規范化,則可以防止第一列在算法中占主導地位。
- for i in range(1, len(X.columns)):
- X[i-1] = X[i-1]/np.max(X[i-1])
- X.head()
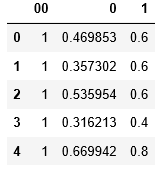
(4) 初始化theta值。我將它們初始化為零。但是任何其他數字都可以。
- theta = np.array([0]*len(X.columns))
- #Output: array([0, 0, 0])
(5) 計算在上式中以m表示的訓練數據的數量:
- m = len(df)
(6) 定義假設函數
- def hypothesis(theta, X):
- return theta*X
(7) 使用上述成本函數的公式定義成本函數
- def computeCost(X, y, theta):
- y1 = hypothesis(theta, X)
- y1=np.sum(y1, axis=1)
- return sum(np.sqrt((y1-y)**2))/(2*47)
(8) 編寫梯度下降函數。此函數將以X,y,theta,學習率(公式中的alpha)和歷元(或迭代)作為輸入。我們需要不斷更新theta值,直到成本函數達到最小值為止。
- def gradientDescent(X, y, theta, alpha, i):
- J = [] #cost function in each iterations
- k = 0
- while k < i:
- y1 = hypothesis(theta, X)
- y1 = np.sum(y1, axis=1)
- for c in range(0, len(X.columns)):
- theta[c] = theta[c] - alpha*(sum((y1-y)*X.iloc[:,c])/len(X))
- j = computeCost(X, y, theta)
- J.append(j)
- k += 1
- return J, j, theta
(9) 使用梯度下降函數獲得最終成本,每次迭代的成本列表以及優化的參數theta。我選擇alpha為0.05。但是您可以嘗試使用其他一些值(例如0.1、0.01、0.03、0.3)來查看會發生什么。我運行了10000次迭代。請嘗試進行更多或更少的迭代,以查看差異。
- J, j, theta = gradientDescent(X, y, theta, 0.05, 10000)
(10) 使用優化的theta預測輸出
- y_hat = hypothesis(theta, X)y_hat = np.sum(y_hat, axis=1)
(11) 繪制原始y和預測輸出y_hat
- %matplotlib inline
- import matplotlib.pyplot as plt
- plt.figure()
- plt.scatter(x=list(range(0, 47)),yy= y, color='blue')
- plt.scatter(x=list(range(0, 47)), y=y_hat, color='black')
- plt.show()
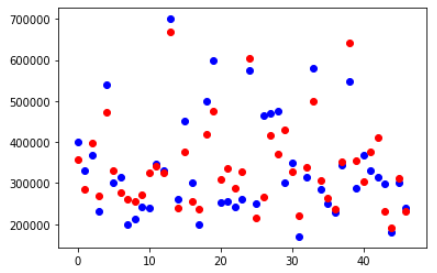
一些輸出點幾乎與預測輸出重疊。有些接近但不重疊。
(12) 繪制每次迭代的成本以查看行為
- plt.figure()
- plt.scatter(x=list(range(0, 10000)), y=J)
- plt.show()
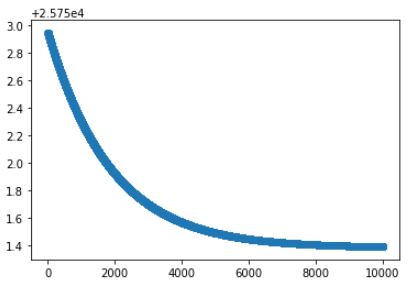
每次迭代的成本都在下降。這表明算法運行良好。
希望對您有所幫助,您也可以自己嘗試一下。我鼓勵您下載數據集,并在閱讀本章以學習機器學習概念時嘗試自己運行所有代碼。這是數據集的鏈接:
https://github.com/rashida048/Machine-Learning-With-Python/blob/master/ex1data2.txt