線性回歸和邏輯回歸是當今很受歡迎的兩種機器學習模型。

[[331887]]

本文將教你如何使用 scikit-learn 庫在Python中創建、訓練和測試你的第一個線性、邏輯回歸機器學習模型，本文適合大部分的新人小白。

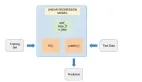
線性回歸機器學習模型

1.要使用的數據集

由于線性回歸是我們在本文中學習的第一個機器學習模型，因此在本文中，我們將使用人工創建的數據集。這能讓你可以更加專注于學習理解機器學習的概念，并避免在清理或處理數據上花費不必要的時間。

更具體地說，我們將使用住房數據的數據集并嘗試預測住房價格。在構建模型之前，我們首先需要導入所需的庫。

2.需要用到的Python庫

我們需要導入的第一個庫是 pandas，它是一個“panel data”的組合體，是處理表格數據比較流行的Python庫。

一般我們會用pd來命名該庫，你可以使用以下語句導入Pandas：

import pandas as pd 

接下來，我們需要導入NumPy，這是一個很常用的數值計算庫。Numpy以其Numpy數組數據結構以及非常有用的reshee、arange和append而聞名。

一般我們也會用np作為Numpy的別名，你可以使用以下語句進行導入：

import numpy as np 

接下來，我們需要導入matplotlib，這是Python很受歡迎的數據可視化庫。

matplotlib通常以別名導入plt。你可以使用以下語句導入：

import matplotlib.pyplot as plt 
 
%matplotlib inline 

該%matplotlib inline語句可以將我們的matplotlib可視化直接嵌入到我們的Jupyter Notebook中，更易于訪問和解釋。

最后，你還要導入seaborn，這是另一個Python數據可視化庫，你可以更輕松地使用matplotlib創建漂亮的可視化數據。

你可以使用以下語句導入：

import seaborn as sns 

總結一下，這是本文必需的庫的導入：

import pandas as pd 
 
import numpy as np 
 
import matplotlib.pyplot as plt 
 
%matplotlib inline 
 
import seaborn as sns 

導入數據集

如前所述，我們將使用住房信息數據集。在下面的URL鏈接中，有我們的.csv文件數據集：

https://nickmccullum.com/files/Housing_Data.csv 

要將數據集導入到Jupyter Notebook中，首先要做的是通過將該URL復制并粘貼到瀏覽器中來下載文件。然后，將文件移到Jupyter Notebook的目錄下。

完成此操作后，以下Python語句可以將住房數據集導入到Jupyter Notebook中：

raw_data = pd.read_csv('Housing_Data.csv') 

該數據集具有許多功能，包括：

• 房屋面積的平均售價
• 該地區平均客房總數
• 房子賣出的價格
• 房子的地址

此數據是隨機生成的，因此你會看到一些可能沒有意義的細微差別(例如，在應該為整數的數字之后的大量小數位)。

了解數據集

現在已經在raw_data變量下導入了數據集，你可以使用該info方法獲取有關數據集的一些高級信息。具體來說，運行raw_data.info()可以得出：

<class 'pandas.core.frame.DataFrame'> 
 
RangeIndex: 5000 entries, 0 to 4999 
 
Data columns (total 7 columns): 
 
Avg. Area Income                5000 non-null float64 
 
Avg. Area House Age             5000 non-null float64 
 
Avg. Area Number of Rooms       5000 non-null float64 
 
Avg. Area Number of Bedrooms    5000 non-null float64 
 
Area Population                 5000 non-null float64 
 
Price                           5000 non-null float64 
 
Address                         5000 non-null object 
 
dtypes: float64(6), object(1) 
 
memory usage: 273.6+ KB 

另一個有用的方法是生成數據。您可以為此使用seaborn方法pairplot，并將整個DataFrame作為參數傳遞。通過下面的一行代碼進行說明：

sns.pairplot(raw_data) 

該語句的輸出如下：

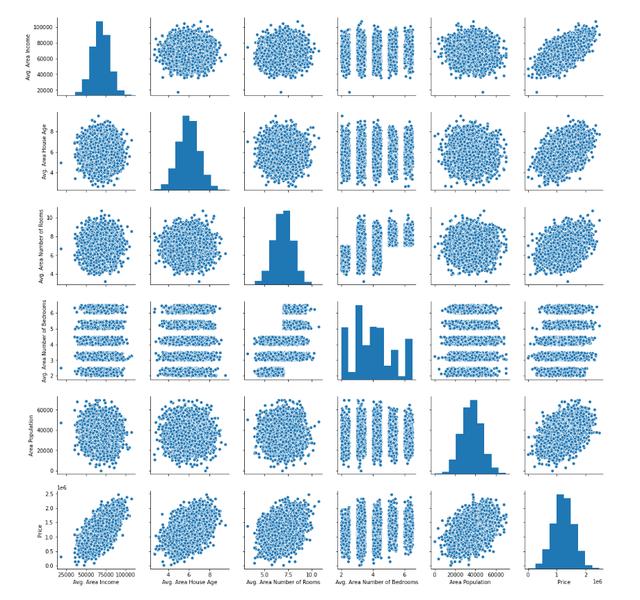
接下來，讓我們開始構建線性回歸模型。

建立機器學習線性回歸模型

我們需要做的第一件事是將我們的數據分為一個x-array(包含我們將用于進行預測y-array的數據)和一個(包含我們正在嘗試進行預測的數據)。

首先，我們應該決定要包括哪些列，你可以使用生成DataFrame列的列表，該列表raw_data.columns輸出：

Index(['Avg. Area Income', 'Avg. Area House Age', 'Avg. Area Number of Rooms', 
 
       'Avg. Area Number of Bedrooms', 'Area Population', 'Price', 'Address'], 
 
      dtype='object') 

x-array除了價格(因為這是我們要預測的變量)和地址(因為它僅包含文本)之外，我們將在所有這些變量中使用。

讓我們創建x-array并將其分配給名為的變量x。

x = raw_data[['Avg. Area Income', 'Avg. Area House Age', 'Avg. Area Number of Rooms', 
 
       'Avg. Area Number of Bedrooms', 'Area Population']] 

接下來，讓我們創建我們的代碼y-array并將其分配給名為的變量y。

y = raw_data['Price'] 

我們已經成功地將數據集劃分為和x-array(分別為模型的輸入值)和和y-array(分別為模型的輸出值)。在下一部分中，我們將學習如何將數據集進一步分為訓練數據和測試數據。

將我們的數據集分為訓練數據和測試數據

scikit-learn 可以很容易地將我們的數據集分為訓練數據和測試數據。為此，我們需要 train_test_split 從中的 model_selection 模塊導入函數 scikit-learn。

這是執行此操作的完整代碼：

from sklearn.model_selection import train_test_split 

該train_test_split數據接受三個參數：

• x-array
• y-array
• 測試數據的期望大小

有了這些參數，該 train_test_split 功能將為我們拆分數據!如果我們想讓測試數據占整個數據集的30%，可以使用以下代碼：

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3) 

讓我們解開這里發生的一切。

train_test_split 函數返回長度為4的Python列表，其中列表中的每個項分別是x_train、x_test、y_train和y_test。然后我們使用列表解包將正確的值賦給正確的變量名。

現在我們已經正確地劃分了數據集，是時候構建和訓練我們的線性回歸機器學習模型了。

建立和訓練模型

我們需要做的第一件事是從scikit learn導入LinearRegression估計器。下面是Python語句：

from sklearn.linear_model import LinearRegression 

接下來，我們需要創建一個線性回歸Python對象的實例。我們將把它賦給一個名為model的變量。下面是代碼：

model = LinearRegression() 

我們可以使用 scikit-learn 中的 fit 方法在訓練數據上訓練該模型。

model.fit(x_train, y_train) 

我們的模型現已訓練完畢，可以使用以下語句檢查模型的每個系數：

print(model.coef_) 

輸出：

[2.16176350e+01 1.65221120e+05 1.21405377e+05 1.31871878e+03 
 
 1.52251955e+01] 

類似地，下面是如何查看回歸方程的截距：

print(model.intercept_) 

輸出：

-2641372.6673013503 

查看系數的更好方法是將它們放在一個數據幀中，可以通過以下語句實現：

pd.DataFrame(model.coef_, x.columns, columns = ['Coeff']) 

這種情況下的輸出更容易理解：

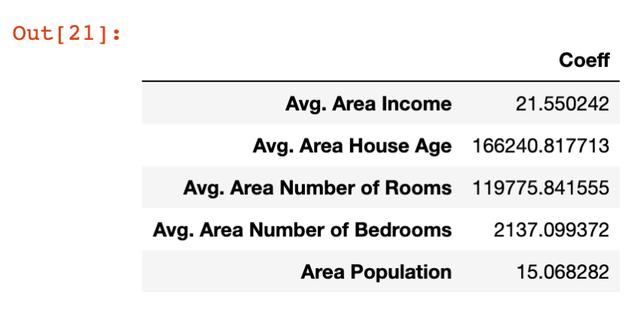
讓我們花點時間來理解這些系數的含義。讓我們具體看看面積人口變量，它的系數約為15。

這意味著，如果你保持所有其他變量不變，那么區域人口增加一個單位將導致預測變量(在本例中為價格)增加15個單位。

換言之，某個特定變量上的大系數意味著該變量對您試圖預測的變量的值有很大的影響。同樣，小值的影響也很小。

現在我們已經生成了我們的第一個機器學習線性回歸模型，現在是時候使用該模型從我們的測試數據集進行預測了。

根據我們的模型做出預測

scikit-learn使得從機器學習模型做出預測變得非常容易，我們只需調用前面創建的模型變量的 predict 方法。

因為 predict 變量是用來進行預測的，所以它只接受一個 x-array 參數，它將為我們生成y值!

以下是使用 predict 方法從我們的模型生成預測所需的代碼：

predictions = model.predict(x_test) 

預測變量保存 x_test 中存儲的要素的預測值。 由于我們使用 train_test_split 方法將實際值存儲在y_test中，因此我們接下來要做的是將預測數組的值與 y_test 的值進行比較。

這里有一種簡單的方法是使用散點圖繪制兩個數組。 使用 plt.scatter 方法可以輕松構建 matplotlib 散點圖。 以下為代碼：

plt.scatter(y_test, predictions) 

這是代碼生成的散點圖：

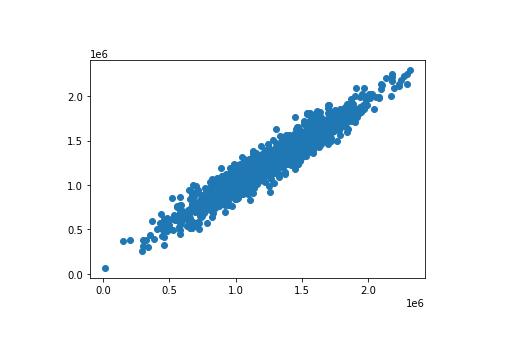
如圖所見，我們的預測值非常接近數據集中觀測值的實際值。在這個散點圖中一條完美的直線表明我們的模型完美地預測了 y-array 的值。

另一種直觀評估模型性能的方法是繪制殘差，即實際y數組值與預測 y-array 值之間的差異。

使用以下代碼語句可以輕松實現：

plt.hist(y_test - predictions) 

以下為代碼生成的可視化效果：

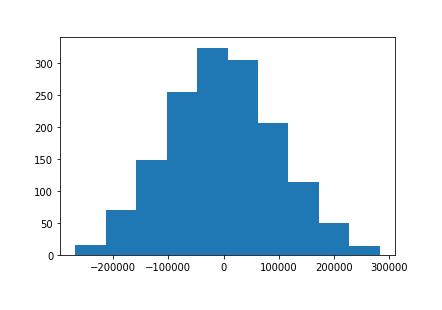
這是我們的機器學習模型殘差的直方圖。

你可能會注意到，我們的機器學習模型中的殘差似乎呈正態分布。這正好是一個很好的信號!

它表明我們已經選擇了適當的模型類型(在這種情況下為線性回歸)來根據我們的數據集進行預測。在本課程的后面，我們將詳細了解如何確保使用了正確的模型。

測試模型的性能

我們在本課程開始時就了解到，回歸機器學習模型使用了三個主要性能指標：

• 平均絕對誤差
• 均方誤差
• 均方根誤差

現在，我們來看看如何為本文中構建的模型計算每個指標。在繼續之前，記得在Jupyter Notebook中運行以下import語句：

from sklearn import metrics 

平均絕對誤差(MAE)

可以使用以下語句計算Python中的平均絕對誤差：

metrics.mean_absolute_error(y_test, predictions) 

均方誤差(MSE)

同樣，你可以使用以下語句在Python中計算均方誤差：

metrics.mean_squared_error(y_test, predictions) 

均方根誤差(RMSE)

與平均絕對誤差和均方誤差不同，scikit learn實際上沒有計算均方根誤差的內置方法。

幸運的是，它真的不需要。由于均方根誤差只是均方根誤差的平方根，因此可以使用NumPy的sqrt方法輕松計算：

np.sqrt(metrics.mean_squared_error(y_test, predictions)) 

附完整代碼

這是此Python線性回歸機器學習教程的全部代碼。

import pandas as pd 
 
import numpy as np 
 
import matplotlib.pyplot as plt 
 
import seaborn as sns 
 
%matplotlib inline 
 
raw_data = pd.read_csv('Housing_Data.csv') 
 
x = raw_data[['Avg. Area Income', 'Avg. Area House Age', 'Avg. Area Number of Rooms', 
 
       'Avg. Area Number of Bedrooms', 'Area Population']] 
 
y = raw_data['Price'] 
 
from sklearn.model_selection import train_test_split 
 
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3) 
 
from sklearn.linear_model import LinearRegression 
 
model = LinearRegression() 
 
model.fit(x_train, y_train) 
 
print(model.coef_) 
 
print(model.intercept_) 
 
pd.DataFrame(model.coef_, x.columns, columns = ['Coeff']) 
 
predictions = model.predict(x_test) 
 
# plt.scatter(y_test, predictions) 
 
plt.hist(y_test - predictions) 
 
from sklearn import metrics 
 
metrics.mean_absolute_error(y_test, predictions) 
 
metrics.mean_squared_error(y_test, predictions) 
 
np.sqrt(metrics.mean_squared_error(y_test, predictions))