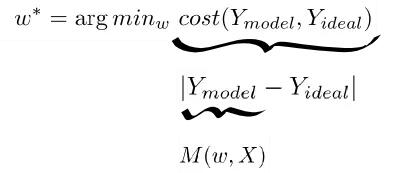初學TensorFlow機器學習:如何實現線性回歸?
TensorFlow 入門級文章:小白也能看懂的TensorFlow介紹
還記得你小學時學習的科學課程嗎?也許就在不久前,誰知道呢——也許你正在上小學,但是已經早早開始了你的機器學習之旅。不管是哪種方式,不管是生物、化學或者物理,一種分析數據的常用技術是用繪圖來觀察一個變量的變化對其它變量的影響。
設想你要繪制降雨頻率與農作物產量間的相關性圖。你也許會觀察到隨著降雨量的增加農業生產率也會增加。通過對這些數據擬合一條線,你可以預測不同降雨條件下的農業生產率。如果你能夠從幾個數據點發現隱式函數關系,那么你就可以利用此學習到的函數來預測未知數據的值。
回歸算法研究的是如何最佳擬合概括數據的曲線。它是有監督學習算法中最強大和被研究最多的一類算法。在回歸中,我們嘗試通過找到可能生成數據的曲線來理解數據。通過這樣做,我們為給定數據散點的分布原因找到了一種解釋。最佳擬合曲線給出了一個解釋數據集是如何生成的模型。
在本文中,你將學習如何用回歸來解決一個實際問題。你將看到,如果你想擁有最強大的預測器,TensorFlow 工具將是正確的選擇。
基本概念
如果你有工具,那么干什么事情都會很容易。我將演示第一個重要的機器學習工具——回歸(regression),并給出精確的數學表達式。首先,你在回歸中學習到的很多技能會幫助你解決可能遇到的其它類型的問題。讀完本文,回歸將成為你的機器學習工具箱中的得力工具。
假設我們的數據記錄了人們在每瓶啤酒瓶上花多少錢。A 花了 2 美元 1 瓶,B 花了 4 美元 2 瓶,C 花了 6 美元 3 瓶。我們希望找到一個方程,能夠描述啤酒的瓶數如何影響總花費。例如,如果每瓶啤酒都花費 2 美元,則線性方程 y=2x 可以描述購買特定數量啤酒的花費。
當一條線能夠很好的擬合一些數據點時,我們可以認為我們的線性模型表現良好。實際上,我們可以嘗試許多可能的斜率,而不是固定選擇斜率值為 2。斜率為參數,產生的方程為模型。用機器學習術語來說,最佳擬合曲線的方程來自于學習模型的參數。
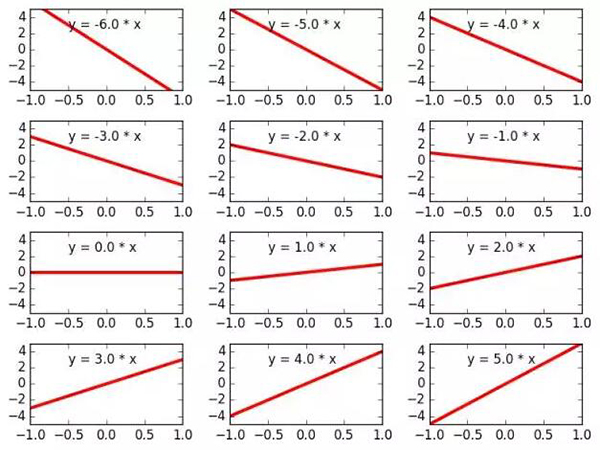
另一個例子,方程 y=3x 也是一條直線,除了具有更陡的斜率。你可以用任何實數替換該系數,這個系數稱為 w,方程仍為一條直線:y=wx。圖 1 顯示了改變參數 w 如何影響模型。我們將這種方式生成的所有方程的集合表示為 M={ y=wx | w∈ℝ}。
這個集合表示「所有滿足 y=wx 的方程,其中 w 是實數」。
圖 1.
圖 1:參數 w 的不同值代表不同的線性方程。所有這些線性方程的集合構成線性模型 M。
M 是所有可能的模型的集合。每選定一個 w 的值就會生成候選模型 M(w):y=wx。在 TensorFlow 中編寫的回歸算法將迭代收斂到更好的模型參數 w。我們稱最佳參數為 w*,最佳擬合方程為 M(w*):y=w*x。
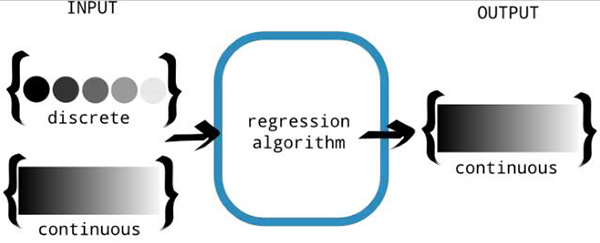
本質上,回歸算法嘗試設計一個函數(讓我們將其稱為 f),將輸入映射到輸出。函數的域是一個實數向量 ℝd,其范圍是實數集 ℝ。函數的輸入可以是連續的或離散的。然而,輸出必須是連續的,如圖 2 所示。
圖 2.
圖 2:回歸算法是為了產生連續的輸出。輸入允許是離散的或連續的。這種區別是重要的,因為離散的輸出值能更適合分類問題,我們將在下一章中討論這個問題。
附帶說明,回歸的預測值為連續輸出,但有時這是過度的。有時我們只想預測一個離散的輸出,例如 0 或 1(0 和 1 之間不產生任何數值)。分類是一種更適合這類任務的技術。
我們希望找到與給定數據(即是輸入/輸出數據對)相一致的函數 f。不幸的是,可能的函數的數量是無限的,所以我們不能一個一個地嘗試。有太多的選擇通常并不是一件好事。需要縮小我們要處理的所有函數的范圍。例如,若我們僅查找擬合數據的直線(不包含曲線),則搜索將變得更加容易。
- 練習 1:將 10 個整數映射到 10 個整數的所有可能函數有多少?例如,令 f(x) 是輸入變量取數字 0 到 9 且輸出為數字 0 到 9 的函數。例如模擬其輸入的恒等函數(identity function),如 f(0)=0,f(1)=1,依此類推。還存在多少其它的函數?
- 答案:10^10=10000000000
如何判斷回歸算法可行?
假設我們正在向房地產公司兜售房地產市場預測算法。該算法在給定一些如臥室數量、公寓面積等房屋屬性后能夠預測房產的價格。房地產公司可以利用房價信息輕松地賺取數百萬美元,但是在購買算法之前他們需要一些算法可行的證據。
衡量訓練后的算法是否成功有兩個重要指標:方差(variance)和偏差(bias)。
方差反映的是預測值對于訓練集的敏感度(波動)。我們希望在理想情況下,訓練集的選擇對結果影響很小——意味著需要較小的方差值。
偏差代表了訓練集假設的可信度。太多的假設可能會難以泛化,所以也需要較小的偏差值。
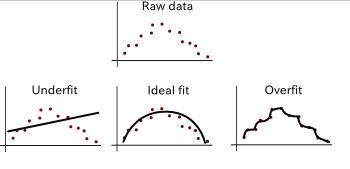
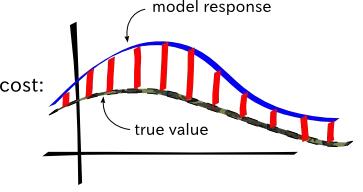
一方面,過于靈活的模型可能導致模型意外地記住訓練集,而不是發現有用的模式特征。你可以想象一個彎曲的函數經過數據集的每個點而不產生錯誤。如果發生這種情況,我們說學習算法對訓練數據過擬合。在這種情況下,最佳擬合曲線將很好地擬合訓練數據;然而,當用測試集進行評估時,結果可能非常糟糕(參見圖 3)。
圖 3
圖 3: 理想情況下,最佳擬合曲線同時適用于訓練集和測試集。然而,如果看到測試集的表現比訓練集更好,那么我們的模型有可能欠擬合。相反,如果在測試集上表現不佳,而對訓練集表現良好,那么我們的模型是過擬合的。
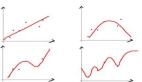
另一方面,不那么靈活的模型可以更好地概括未知的測試數據,但是在訓練集上表現欠佳。這種情況稱為欠擬合。一個過于靈活的模型具有高方差和低偏差,而一個不靈活的模型具有低方差和高偏差。理想情況下,我們想要一個具有低方差誤差和低偏差誤差的模型。這樣一來,它們就能夠概括未知的數據并捕獲數據的規律性。參見圖 4 的例子。
圖 4. 數據欠擬合和過擬合的例子。
具體來說,模型的方差是衡量響應的波動程度有多大的一個標準,偏差是響應與實際數據相差的程度。最后,希望模型達到準確(低偏差)和可重復(低方差)的效果。
- 練習 2:假設我們的模型為 M(w):y=wx。如果權重 w 的值必須為 0-9 之間的整數,則有多少個可能的函數?
- 答案:只有 10 種情況,即 { y=0,y=x,y=2x,...,y=9x }。
為了評估機器學習模型,我們將數據集分為兩組:訓練集和測試集。訓練集用來學習模型,測試集用來評估性能。存在很多可能的權重參數,但我們的目標是找到最適合數據的權重。用來衡量「最適合」的方式是定義成本函數(cost function)。
線性回歸
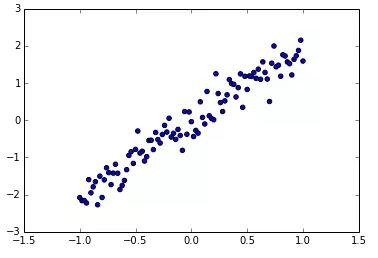
讓我們利用模擬數據來進行線性回歸。創建一個名為 regression.py 的 Python 源文件,并按照列表 1 初始化數據。代碼將產生類似于圖 5 的輸出。
列表 1:可視化原始輸入
- import numpy as np //#Aimport matplotlib.pyplot as plt //#B
- x_train = np.linspace(-1, 1, 101) //#C
- y_train = 2 * x_train + np.random.randn(*x_train.shape) * 0.33 //#D
- plt.scatter(x_train, y_train) //#E
- plt.show() //#E
- # A:導入 NumPy 包,用來生成初始化的原始數據
- # B:使用 matplotlib 可視化數據
- # C:輸入值為 -1 到 1 之間的 101 個均勻間隔的數字
- # D:生成輸出值,與輸入值成正比并附加噪聲
- # E:使用 matplotlib 的函數繪制散點圖
圖 5. 散點圖 y=x+ε,ε 為噪聲。
現在你可以利用這些數據點嘗試擬合一條直線。在 TensorFlow 中,你至少需要為嘗試的每個候選參數打分。該打分通常稱為成本函數。成本函數值越高,模型參數越差。例如,如果最佳擬合直線為 y=2x,選擇參數值為 2.01 時應該有較低的成本函數值,但是選擇參數值為 -1 時應該具有較高的成本函數值。
這時,我們的問題就轉化為最小化成本函數值,如圖 6 所示,TensorFlow 試圖以有效的方式更新參數,并最終達到最佳的可能值。每個更新所有參數的步驟稱為 epoch。
圖 6
圖 6:無論哪個參數 w,最優的成本函數值都是最小的。成本函數的定義是真實值與模型響應之間的誤差的范數(norm,可以是 2 次方、絕對值、3 次方……)。最后,響應值由模型的函數計算得出。
在本例中,成本函數定義為誤差的和(sum of errors)。通常用實際值 f(x) 與預測值 M(w,x) 之間的平方差來計算預測 x 的誤差。因此,成本函數值是實際值和預測值之間的平方差之和,如圖 7 所示。
圖 7. 成本函數值是模型響應與真實值之間的逐點差異的范數。
更新列表 1 中的代碼,見列表 2。該代碼定義了成本函數,并要求 TensorFlow 運行(梯度下降)優化來找到最佳的模型參數。
列表 2:求解線性回歸
- import tensorflow as tf //#Aimport numpy as np //#Aimport matplotlib.pyplot as plt //#A
- learning_rate = 0.01 //#B
- training_epochs = 100 //#B
- x_train = np.linspace(-1, 1, 101) //#C
- y_train = 2 * x_train + np.random.randn(*x_train.shape) * 0.33 //#C
- X = tf.placeholder("float") //#D
- Y = tf.placeholder("float") //#Ddef model(X, w): //#E return tf.multiply(X, w)
- w = tf.Variable(0.0, name="weights") //#F
- y_model = model(X, w) //#G
- cost = tf.square(Y-y_model) //#G
- train_op = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) //#H
- sess = tf.Session() //#I
- init = tf.global_variables_initializer() //#I
- sess.run(init) //#Ifor epoch in range(training_epochs): //#J for (x, y) in zip(x_train, y_train): //#K
- sess.run(train_op, feed_dict={X: x, Y: y}) //#L
- w_val = sess.run(w) //#M
- sess.close() //#N
- plt.scatter(x_train, y_train) //#O
- y_learned = x_train*w_val //#P
- plt.plot(x_train, y_learned, 'r') //#P
- plt.show() //#P
- #A:載入 TensorFlow 包用于學習算法,載入 NumPy 包來設置初始數據,載入 matplotlib 包來可視化數據
- #B:定義學習算法使用的一些常數,稱為超參數
- #C:初始化線性模擬數據
- #D:將輸入和輸出節點設置為占位符,而真實數值將傳入 x_train 和 y_train
- #E:將模型定義為 y=w*x
- #F:設置權重變量
- #G:定義成本函數
- #H:定義在學習算法的每次迭代中將被調用的操作
- #I:設置會話并初始化所有變量
- #J:多次循環遍歷數據集
- #K:循環遍歷數據集中的每個數據
- #L:更新模型參數以嘗試最小化成本函數
- #M:得到最終參數值
- #N:關閉會話
- #O:繪制原始數據
- #P:繪制最佳擬合直線
恭喜你使用 TensorFlow 解決了線性回歸!另外,只需要對列表 2 稍加修改就能解決回歸中的其它問題。整個流程包括使用 TensorFlow 更新模型參數,如圖 8 所示。
圖 8. 學習算法更新模型的參數以最小化給定的成本函數。
原文:https://machinelearning.technicacuriosa.com/2017/04/22/machine-learning-with-tensorflow/
【本文是51CTO專欄機構機器之心的原創譯文,微信公眾號“機器之心( id: almosthuman2014)”】