MySQL索引底層:B+樹詳解
前言
當我們發現SQL執行很慢的時候,自然而然想到的就是加索引。對于范圍查詢,索引的底層結構就是B+樹。今天我們一起來學習一下B+樹哈~
- 樹簡介、樹種類
- B-樹、B+樹簡介
- B+樹插入
- B+樹查找
- B+樹刪除
- B+樹經典面試題
樹的簡介
樹的簡介
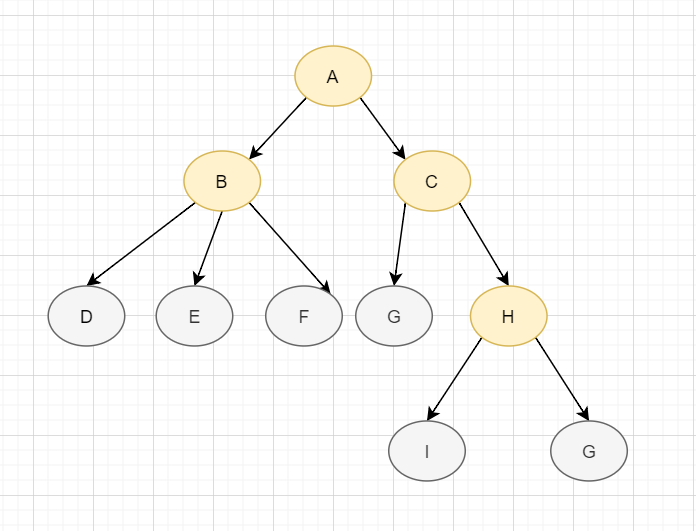
樹跟數組、鏈表、堆棧一樣,是一種數據結構。它由有限個節點,組成具有層次關系的集合。因為它看起來像一棵樹,所以得其名。一顆普通的樹如下:
樹是包含n(n為整數,大于0)個結點, n-1條邊的有窮集,它有以下特點:
- 每個結點或者無子結點或者只有有限個子結點;
- 有一個特殊的結點,它沒有父結點,稱為根結點;
- 每一個非根節點有且只有一個父節點;
- 樹里面沒有環路
一些有關于樹的概念:
- 結點的度:一個結點含有的子結點個數稱為該結點的度;
- 樹的度:一棵樹中,最大結點的度稱為樹的度;
- 父結點:若一個結點含有子結點,則這個結點稱為其子結點的父結點;
- 深度:對于任意結點n,n的深度為從根到n的唯一路徑長,根結點的深度為0;
- 高度:對于任意結點n,n的高度為從n到一片樹葉的最長路徑長,所有樹葉的高度為0;
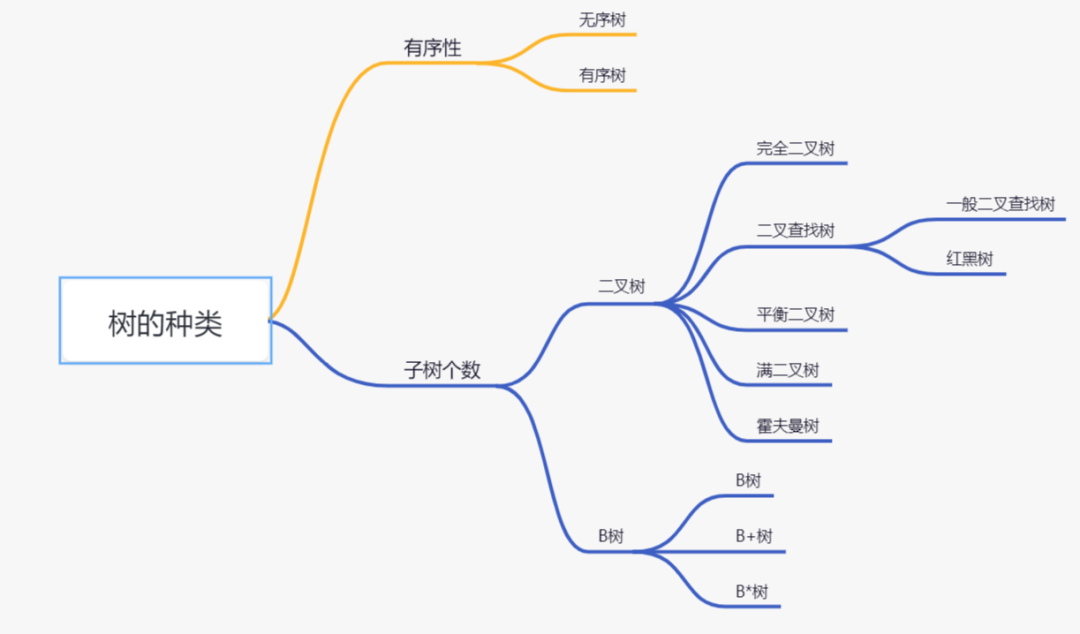
樹的種類
按照有序性,可以分為有序樹和無序樹:
- 無序樹:樹中任意節點的子結點之間沒有順序關系
- 有序樹:樹中任意節點的子結點之間有順序關系
按照節點包含子樹個數,可以分為B樹和二叉樹,二叉樹可以分為以下幾種:
- 二叉樹:每個節點最多含有兩個子樹的樹稱為二叉樹;
- 二叉查找樹:首先它是一顆二叉樹,若左子樹不空,則左子樹上所有結點的值均小于它的根結點的值;若右子樹不空,則右子樹上所有結點的值均大于它的根結點的值;左、右子樹也分別為二叉排序樹;
- 滿二叉樹:葉節點除外的所有節點均含有兩個子樹的樹被稱為滿二叉樹;
- 完全二叉樹:如果一顆二叉樹除去最后一層節點為滿二叉樹,且最后一層的結點依次從左到右分布
- 霍夫曼樹:帶權路徑最短的二叉樹。
- 紅黑樹:紅黑樹是一顆特殊的二叉查找樹,每個節點都是黑色或者紅色,根節點、葉子節點是黑色。如果一個節點是紅色的,則它的子節點必須是黑色的。
- 平衡二叉樹(AVL):一 棵空樹或它的左右兩個子樹的高度差的絕對值不超過1,并且左右兩個子樹都是一棵平衡二叉樹
B-樹、B+樹簡介
B-樹簡介
B-樹,也稱為B樹,是一種平衡的多叉樹(可以對比一下平衡二叉查找樹),它比較適用于對外查找。看下這幾個概念哈:
- 階數:一個節點最多有多少個孩子節點。(一般用字母m表示)
- 關鍵字:節點上的數值就是關鍵字
- 度:一個節點擁有的子節點的數量。
一顆m階的B-樹,有以下特征:
- 根結點至少有兩個子女;
- 每個非根節點所包含的關鍵字個數 j 滿足:⌈m/2⌉ - 1 <= j <= m - 1.(⌈⌉表示向上取整)
- 有k個關鍵字(關鍵字按遞增次序排列)的非葉結點恰好有k+1個孩子。
- 所有的葉子結點都位于同一層。
一棵簡單的B-樹如下:
B+ 樹簡介
B+樹是B-樹的變體,也是一顆多路搜索樹。一棵m階的B+樹主要有這些特點:
- 每個結點至多有m個子女;
- 非根節點關鍵值個數范圍:⌈m/2⌉ - 1 <= k <= m-1
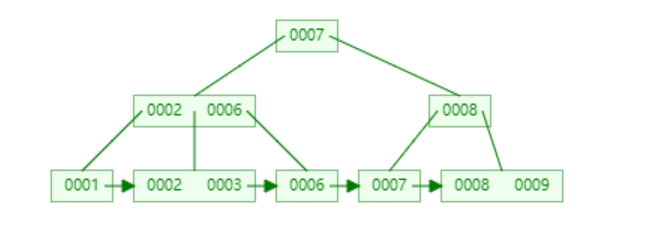
- 相鄰葉子節點是通過指針連起來的,并且是關鍵字大小排序的。
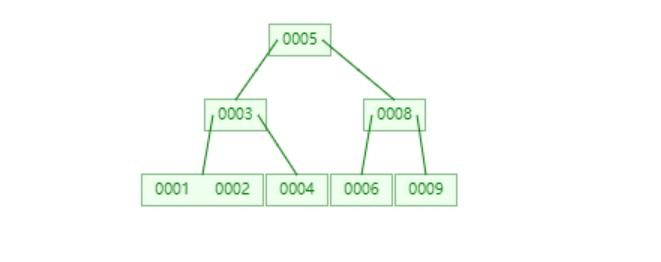
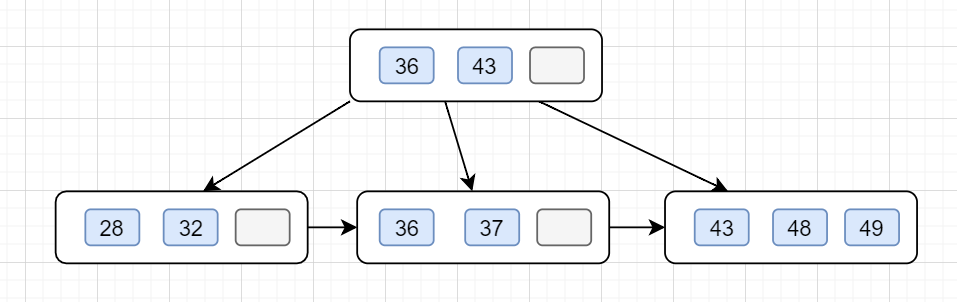
一顆3階的B+樹如下:
B+樹和B-樹的主要區別如下:
- B-樹內部節點是保存數據的;而B+樹內部節點是不保存數據的,只作索引作用,它的葉子節點才保存數據。
- B+樹相鄰的葉子節點之間是通過鏈表指針連起來的,B-樹卻不是。
- 查找過程中,B-樹在找到具體的數值以后就結束,而B+樹則需要通過索引找到葉子結點中的數據才結束
- B-樹中任何一個關鍵字出現且只出現在一個結點中,而B+樹可以出現多次。
B+樹的插入
B+樹插入要記住這幾個步驟:
- 1.B+樹插入都是在葉子結點進行的,就是插入前,需要先找到要插入的葉子結點。
- 2.如果被插入關鍵字的葉子節點,當前含有的關鍵字數量是小于階數m,則直接插入。
- 3.如果插入關鍵字后,葉子節點當前含有的關鍵字數目等于階數m,則插,該節點開始「分裂」為兩個新的節點,一個節點包含⌊m/2⌋ 個關鍵字,另外一個關鍵字包含⌈m/2⌉個關鍵值。(⌊m/2⌋表示向下取整,⌈m/2⌉表示向上取整,如⌈3/2⌉=2)。
- 4.分裂后,需要將第⌈m/2⌉的關鍵字上移到父結點。如果這時候父結點中包含的關鍵字個數小于m,則插入操作完成。
- 5.分裂后,需要將⌈m/2⌉的關鍵字上移到父結點。如果父結點中包含的關鍵字個數等于m,則繼續分裂父結點。
以一顆4階的B+樹為例子吧,4階的話,關鍵值最多3(m-1)個。假設插入以下數據43,48,36,32,37,49,28.
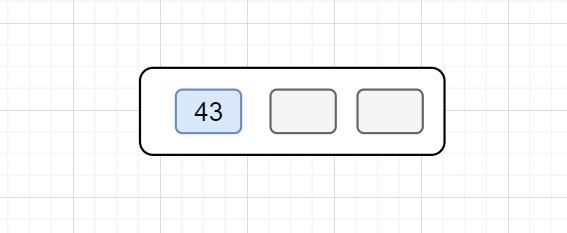
1.在空樹中插入43
這時候根結點就一個關鍵值,此時它是根結點也是葉子結點。
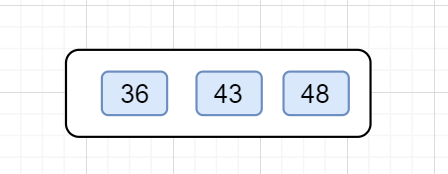
2.依次插入48,36
這時候跟節點擁有3個關鍵字,已經滿了
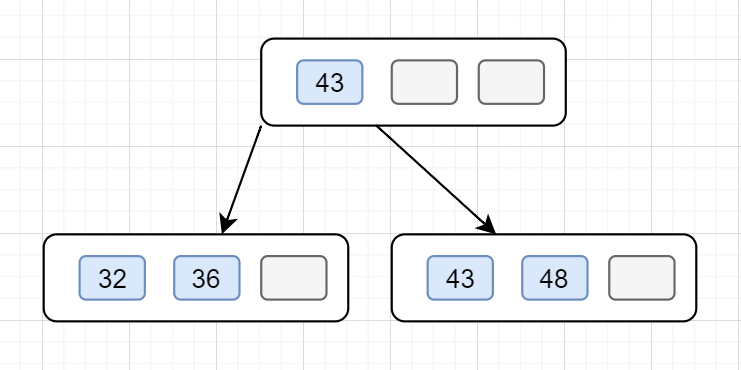
3.繼續插入 32,發現當前節點關鍵字已經不小于階數4了,于是分裂 第⌈4/2⌉=2(下標0,1,2)個,也即43上移到父節點。
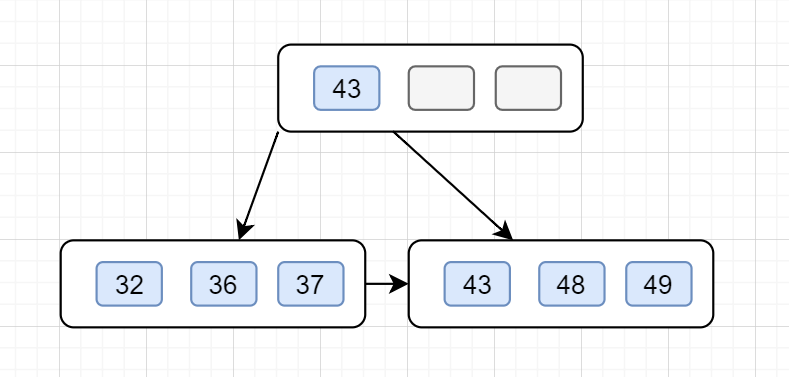
4.繼續插入37,49,前節點關鍵字都是還沒滿的,直接插入,如下:
5.最后插入28,發現當前節點關鍵字也是不小于階數4了,于是分裂,于是分裂, 第 ⌈4/2⌉=2個,也就是36上移到父節點,因父子節點只有2個關鍵值,還是小于4的,所以不用繼續分裂,插入完成
B+樹的查找
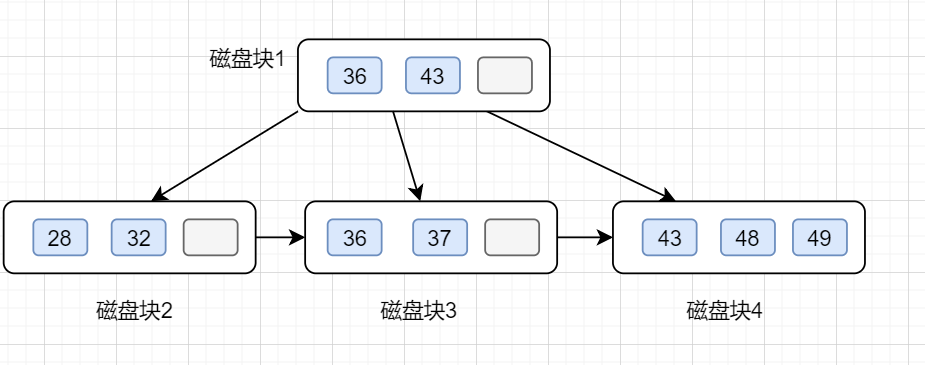
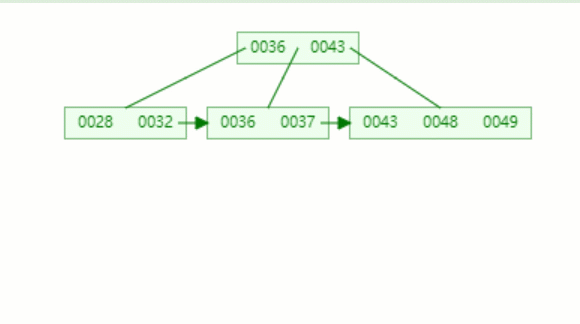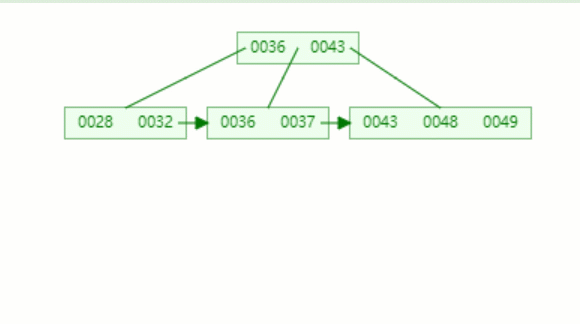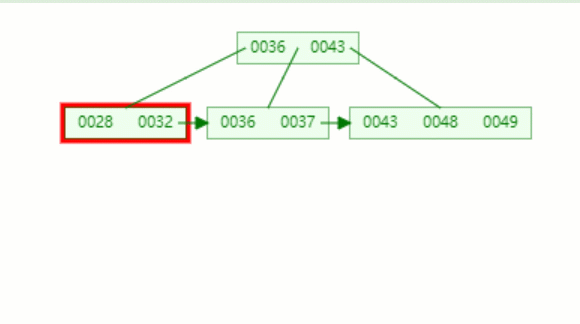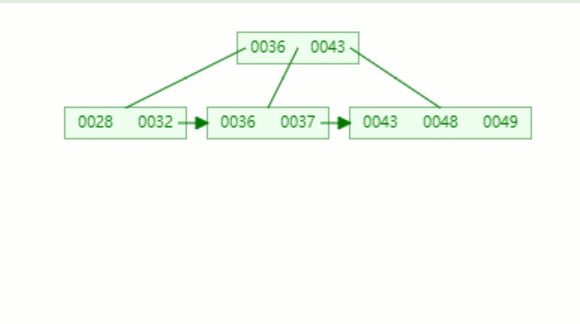
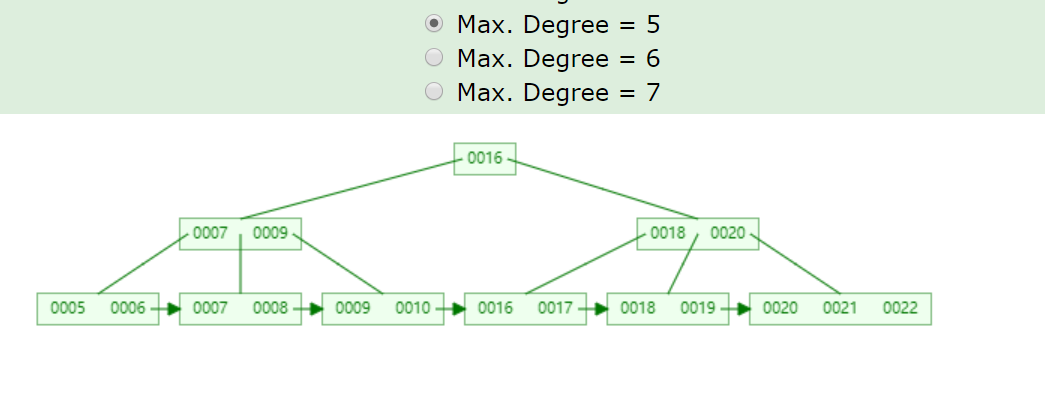
因為B+樹的數據都是在葉子節點上的,內部節點只是指針索引的作用,因此,查找過程需要搜索到葉子節點上。還是以這顆B+樹為例吧:
B+ 樹單值查詢
假設我們要查的值為32.
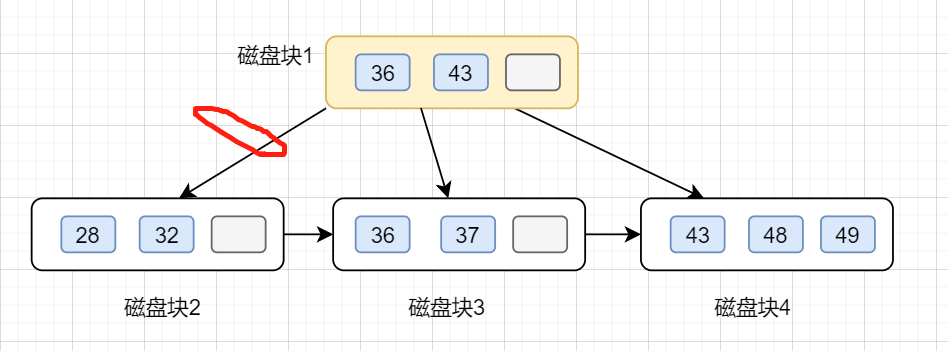
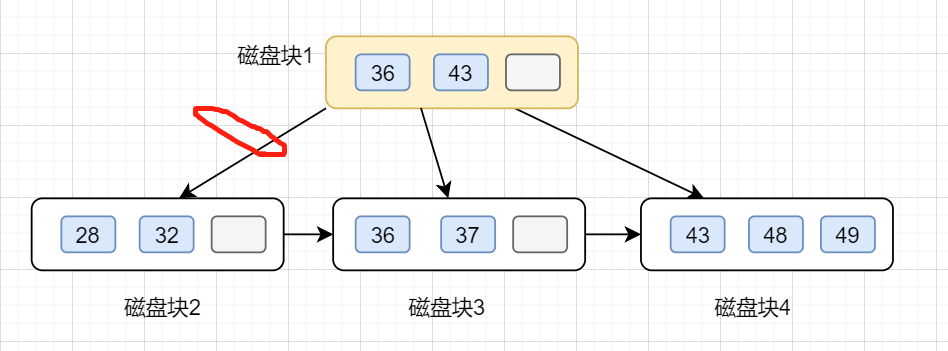
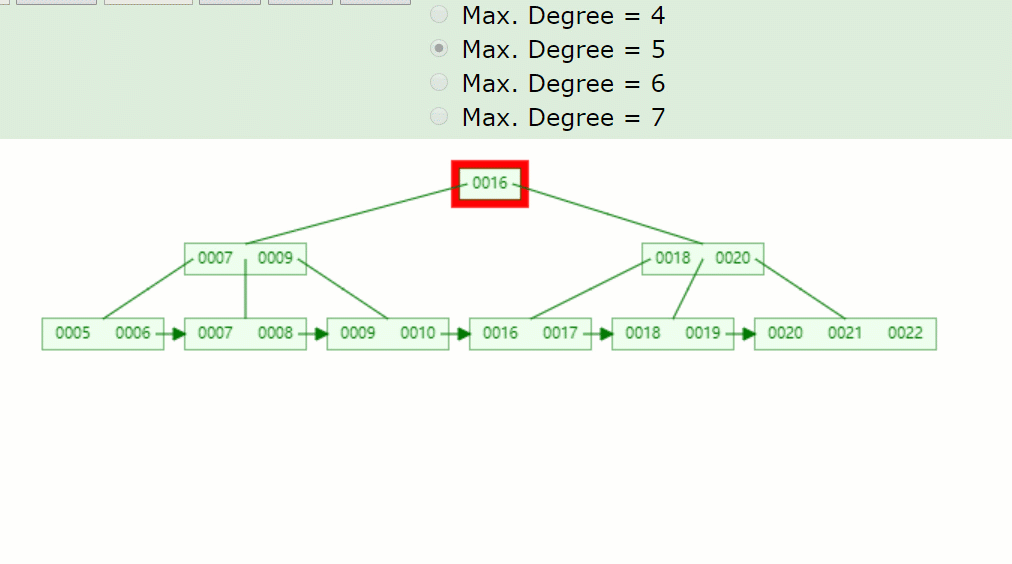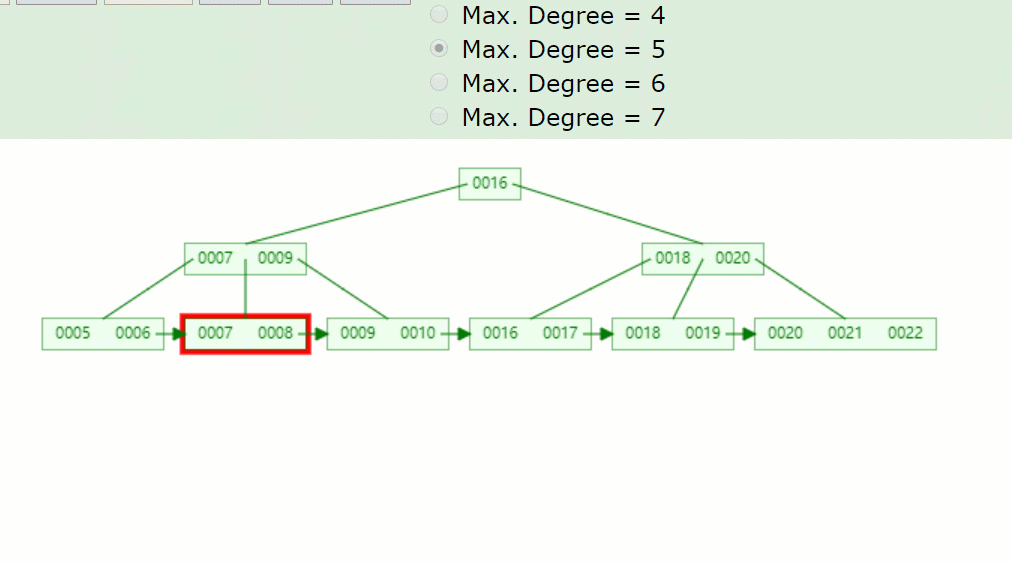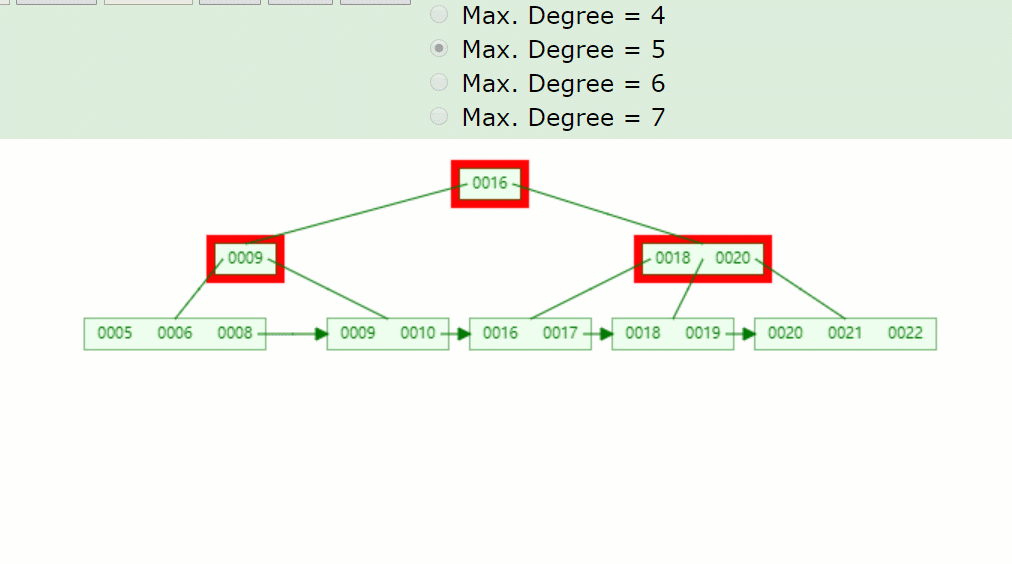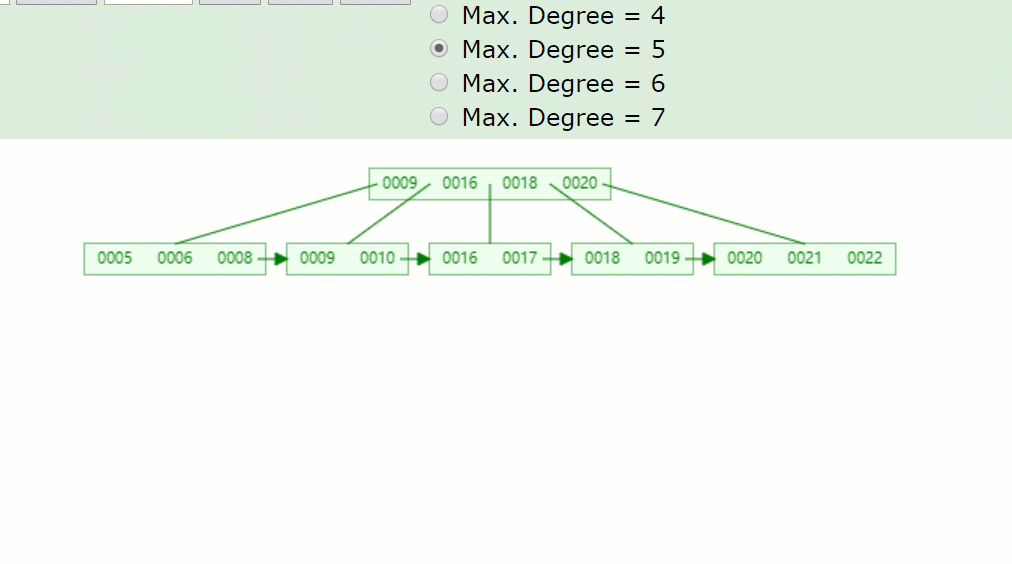
第一次磁盤 I/O,查找磁盤塊1,即根節點(36,43),因為32小于36,因此訪問根節點的左邊第一個孩子節點
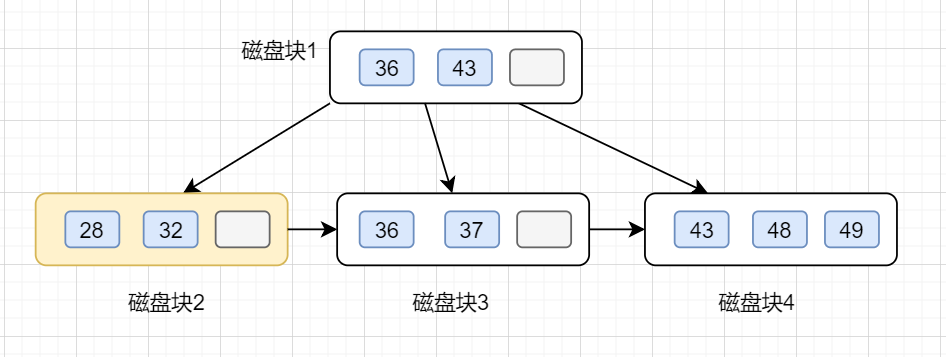
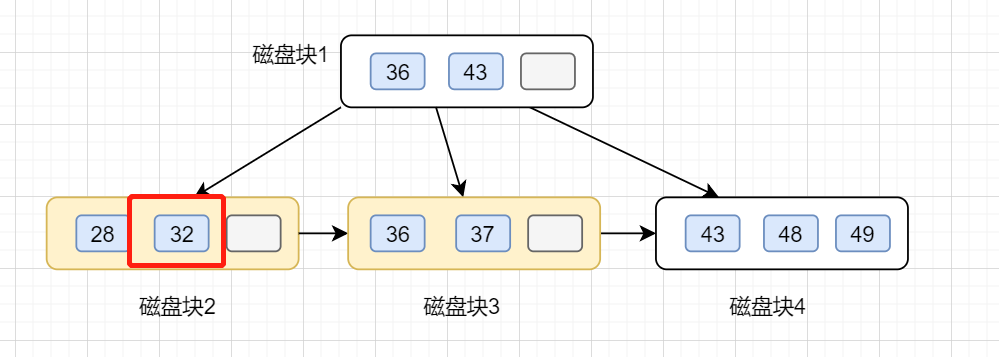
第二次磁盤 I/O, 查找磁盤塊2,即根節點的第一個孩子節點,獲得區間(28,32),遍歷即可得32.
動態圖如下:
B+ 樹范圍查詢
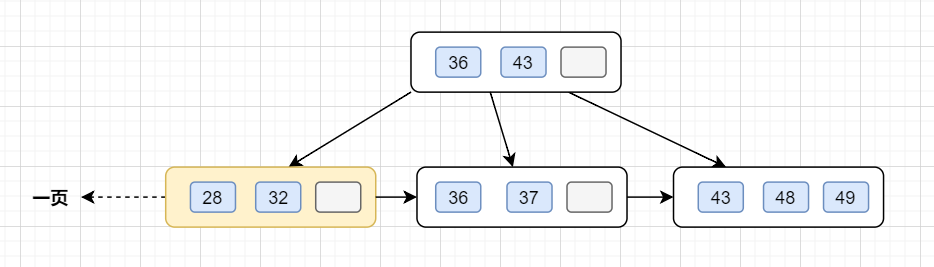
假設我們要查找區間 [32,40]區間的值.
第一步先訪問根節點,發現區間的左端點32小于36,則訪問根節點的第一個左子樹(28,32);
第二步訪問節點(28,32),找到32,于是開始遍歷鏈表,把[32,40]區間值找出來,這也是B+樹比B-樹高效的地方。
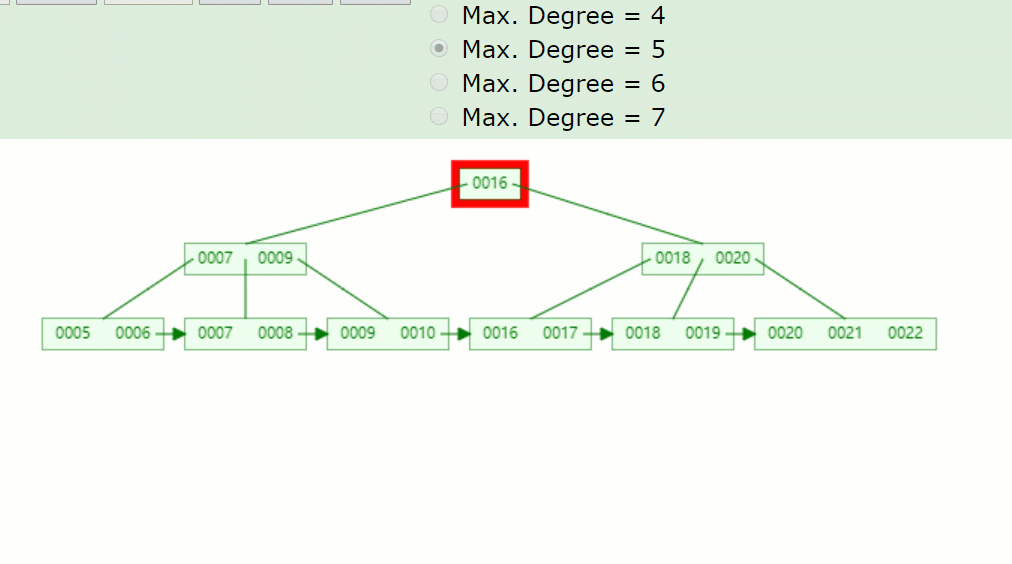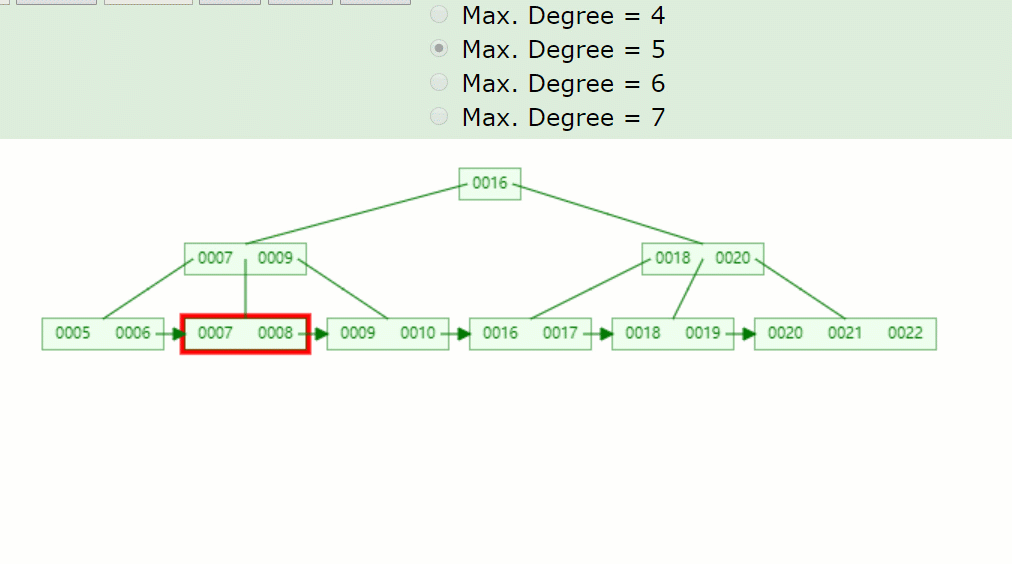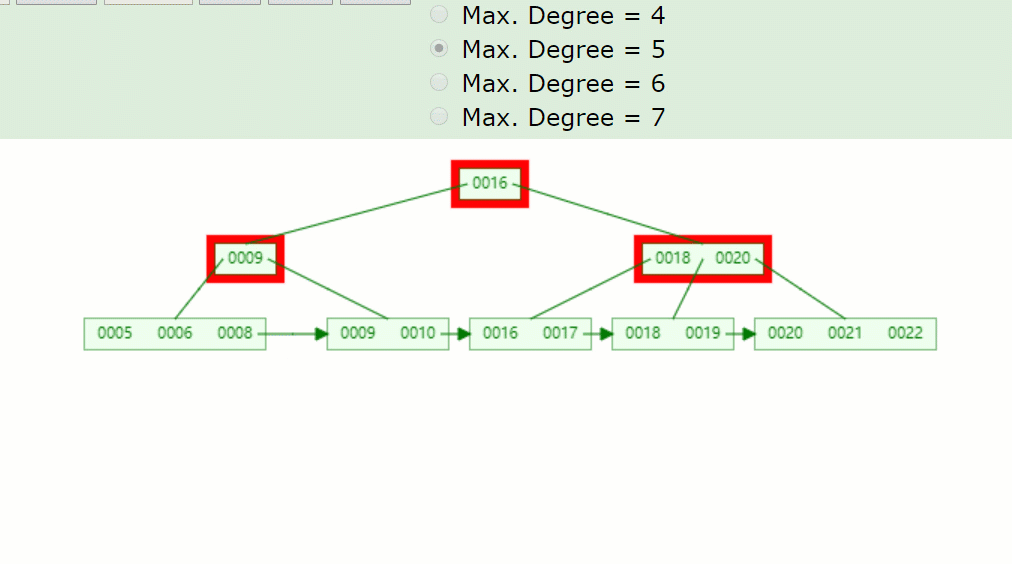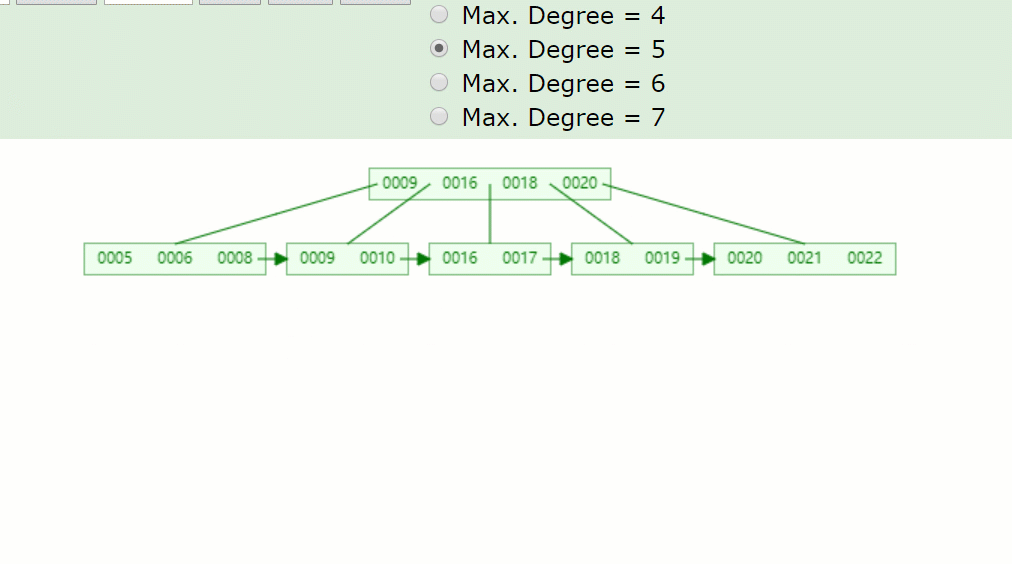
B+樹的刪除
B+樹刪除關鍵字,分這幾種情況
- 找到包含關鍵值的結點,如果關鍵字個數大于⌈m/2⌉-1,直接刪除即可;
- 找到包含關鍵值的結點,如果關鍵字個數大于⌈m/2⌉-1,并且關鍵值是當前節點的最大(小)值,并且該關鍵值存在父子節點中,那么刪除該關鍵字,同時需要相應調整父節點的值。
- 找到包含關鍵值的結點,如果刪除該關鍵字后,關鍵字個數小于⌈m/2⌉,并且其兄弟結點有多余的關鍵字,則從其兄弟結點借用關鍵字
- 找到包含關鍵值的結點,如果刪除該關鍵字后,關鍵字個數小于⌈m/2⌉,并且其兄弟結點沒有多余的關鍵字,則與兄弟結點合并。
如果關鍵字個數大于⌈m/2⌉,直接刪除即可;
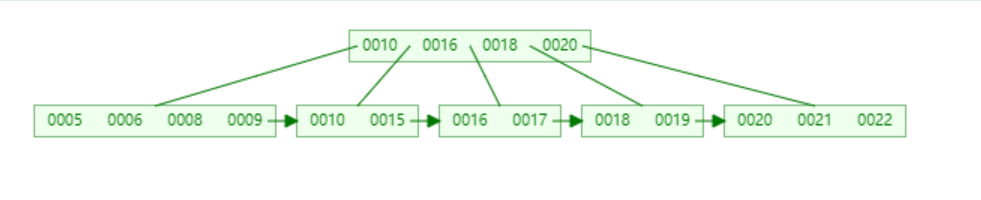
假設當前有這么一顆5階的B+樹
如果刪除22,因為關鍵字個數為3 > ⌈5/2⌉-1=2, 直接刪除(⌈⌉表示向上取整的意思)
如果關鍵字個數大于⌈m/2⌉-1,并且刪除的關鍵字存在于父子節點中,那么需要相應調整父子節點的值
如果刪除20,因為關鍵字個數為3 > ⌈5/2⌉-1=2,并且20是當前節點的邊界值,且存在父子節點中,所以刪除后,其父子節點也要響應調整。
如果刪除該關鍵字后,關鍵字個數小于⌈m/2⌉-1,兄弟節點可以借用
以下這顆5階的B+樹,
如果刪除15,刪除關鍵字的結點只剩1個關鍵字,小于⌈5/2⌉-1=2,不滿足B+樹特點,但是其兄弟節點擁有3個元素(7,8,9),可以借用9過來,如圖:
在刪除關鍵字后,如果導致其結點中關鍵字個數不足,并且兄弟結點沒有得借用的話,需要合并兄弟結點
以下這顆5階的B+樹:
如果刪除關鍵字7,刪除關鍵字的結點只剩1個關鍵字,小于⌈5/2⌉-1=2,不滿足B+樹特點,并且兄弟結點沒法借用,因此發生合并,如下:
主要流程醬紫:
- 因為7被刪掉后,只剩一個8的關鍵字,不滿足B+樹特點(⌈m/2⌉-1<=關鍵字<=m-1)。
- 并且沒有兄弟結點關鍵字借用,因此8與前面的兄弟結點結合。
- 被刪關鍵字結點的父節點,7索引也被刪掉了,只剩一個9,并且其右兄弟結點(18,20)只有兩個關鍵字,也是沒得借,因此在此合并。
- 被刪關鍵字結點的父子節點,也和其兄弟結點合并后,只剩一個子樹分支,因此根節點(16)也下移了。
所以刪除關鍵字7后的結果如下:
B+樹經典面試題
- InnoDB一棵B+樹可以存放多少行數據?
- 為什么索引結構默認使用B+樹,而不是hash,二叉樹,紅黑樹,B-樹?
- B-樹和B+樹的區別
InnoDB一棵B+樹可以存放多少行數據?
這個問題的簡單回答是:約2千萬行。
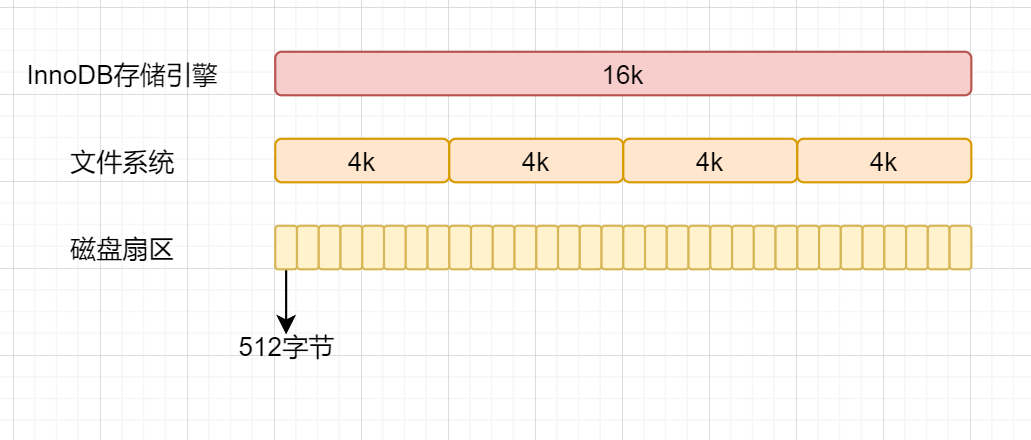
- 在計算機中,磁盤存儲數據最小單元是扇區,一個扇區的大小是512字節。
- 文件系統中,最小單位是塊,一個塊大小就是4k;
- InnoDB存儲引擎最小儲存單元是頁,一頁大小就是16k。
因為B+樹葉子存的是數據,內部節點存的是鍵值+指針。索引組織表通過非葉子節點的二分查找法以及指針確定數據在哪個頁中,進而再去數據頁中找到需要的數據;
假設B+樹的高度為2的話,即有一個根結點和若干個葉子結點。這棵B+樹的存放總記錄數為=根結點指針數*單個葉子節點記錄行數。
- 如果一行記錄的數據大小為1k,那么單個葉子節點可以存的記錄數 =16k/1k =16.
- 非葉子節點內存放多少指針呢?我們假設主鍵ID為bigint類型,長度為8字節,而指針大小在InnoDB源碼中設置為6字節,所以就是8+6=14字節,16k/14B =16*1024B/14B = 1170
因此,一棵高度為2的B+樹,能存放1170 * 16=18720條這樣的數據記錄。同理一棵高度為3的B+樹,能存放1170 *1170 *16 =21902400,也就是說,可以存放兩千萬左右的記錄。B+樹高度一般為1-3層,已經滿足千萬級別的數據存儲。
為什么索引結構默認使用B+樹,而不是B-Tree,Hash哈希,二叉樹,紅黑樹?
簡單版回答如下:
- Hash哈希,只適合等值查詢,不適合范圍查詢。
- 一般二叉樹,可能會特殊化為一個鏈表,相當于全表掃描。
- 紅黑樹,是一種特化的平衡二叉樹,MySQL 數據量很大的時候,索引的體積也會很大,內存放不下的而從磁盤讀取,樹的層次太高的話,讀取磁盤的次數就多了。
- B-Tree,葉子節點和非葉子節點都保存數據,相同的數據量,B+樹更矮壯,也是就說,相同的數據量,B+樹數據結構,查詢磁盤的次數會更少。
B-樹和B+樹的區別
- B-樹內部節點是保存數據的;而B+樹內部節點是不保存數據的,只作索引作用,它的葉子節點才保存數據。
- B+樹相鄰的葉子節點之間是通過鏈表指針連起來的,B-樹卻不是。
- 查找過程中,B-樹在找到具體的數值以后就結束,而B+樹則需要通過索引找到葉子結點中的數據才結束
- B-樹中任何一個關鍵字出現且只出現在一個結點中,而B+樹可以出現多次。
參考與感謝
- B+樹看這一篇就夠了[1]
- B樹和B+樹的插入、刪除圖文詳解[2]
- InnoDB一棵B+樹可以存放多少行數據?[3]
本文轉載自微信公眾號「撿田螺的小男孩」,可以通過以下二維碼關注。轉載本文請聯系撿田螺的小男孩公眾號。