結合隨機微分方程,多大Duvenaud團隊提出無限深度貝葉斯神經網絡
把神經網絡的限制視為無限多個殘差層的組合,這種觀點提供了一種將其輸出隱式定義為常微分方程 ODE 的解的方法。連續深度參數化將模型的規范與其計算分離。雖然范式的復雜性增加了,但這種方法有幾個好處:(1)通過指定自適應計算的容錯,可以以細粒度的方式用計算成本換取精度;(2)通過及時運行動態 backward 來重建反向傳播所需中間狀態的激活函數,可以使訓練的內存成本顯著降低。
另一方面,對神經網絡的貝葉斯處理改動了典型的訓練 pipeline,不再執行點估計,而是推斷參數的分布。雖然這種方法增加了復雜性,但它會自動考慮模型的不確定性——可以通過模型平均來對抗過擬合和改進模型校準,尤其是對于分布外數據。
近日,來自多倫多大學和斯坦福大學的一項研究表明貝葉斯連續深度神經網絡的替代構造具有一些額外的好處,開發了一種在連續深度貝葉斯神經網絡中進行近似推理的實用方法。該論文的一作是多倫多大學 Vector Institute 的本科學生 Winnie Xu,二作是 NeurIPS 2018 最佳論文的一作陳天琦,他們的導師 David Duvenaud 也是論文作者之一。
 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">- 論文地址:https://arxiv.org/pdf/2102.06559.pdf
- 項目地址:https://github.com/xwinxu/bayesian-sde
具體來說,該研究考慮了無限深度貝葉斯神經網絡每層分別具有未知權重的限制,提出一類稱為 SDE-BNN(SDE- Bayesian neural network )的模型。該研究表明,使用 Li 等人(2020)描述的基于可擴展梯度的變分推理方案可以有效地進行近似推理。
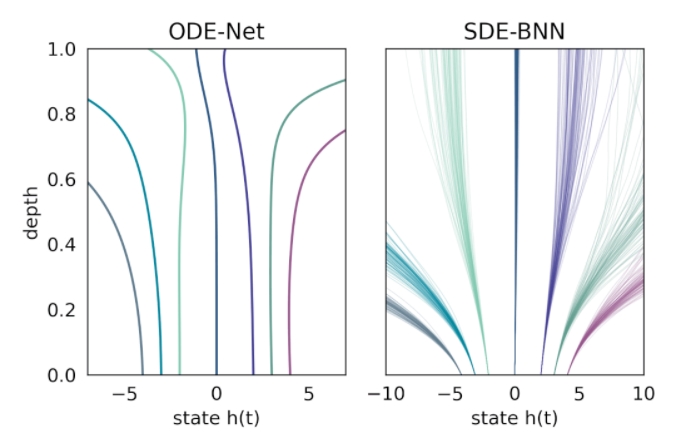
在這種方法中,輸出層的狀態由黑盒自適應隨機微分方程(SDE 求解器計算,并訓練模型以最大化變分下界。下圖將這種神經 SDE 參數化與標準神經 ODE 方法進行了對比。這種方法保持了訓練貝葉斯神經 ODE 的自適應計算和恒定內存成本。
無限深度貝葉斯神經網絡(BNN)
標準離散深度殘差網絡可以被定義為以下形式的層的組合:
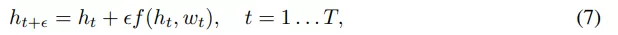 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">其中 t 是層索引,
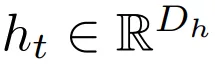 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">表示 t 層隱
藏單元激活向量,輸入 h_0 = x,
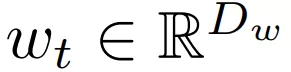 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">表示 t 層的參數,在離散設置中
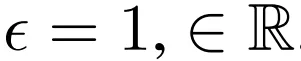 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">該研究通過設置
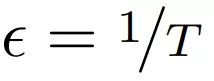 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">并將極限
設為
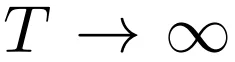 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">來構建殘差網絡的連續深度變體。 這樣產生一個微分方程,該方程將隱藏單元進化描述為深度 t 的函數。 由于標準殘差網絡每層使用不同的權重進行參數化,因此該研究用 w_t 表示第 t 層的權重。此外該研究還引入一個超網絡(hypernetwork) f_w,它將權重的變化指定為深度和當前權重的函數。然后將隱藏單元激活函數的進化和權重組合成一個微分方程:
 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">權重先驗過程:該研究使用 Ornstein-Uhlenbeck (OU) 過程作為權重先驗,該過程的特點是具有漂移(drift)和彌散(diffusion)的 SDE:
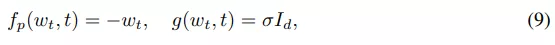 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">權重近似后驗使用另一個具有以下漂移函數的 SDE 隱式地進行參數化:
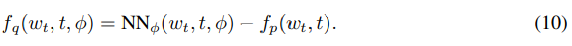 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">然后該研究在給定輸入下評估了該網絡需要邊緣化權重和隱藏單元軌跡(trajectory)。這可以通過簡單的蒙特卡羅方法來完成,從后驗過程中采樣權重路徑 {w_t},并在給定采樣權重和輸入的情況下評估網絡激活函數 {h_t}。這兩個步驟都需要求解一個微分方程,兩步可以通過調用增強狀態 SDE 的單個 SDE 求解器同時完成:
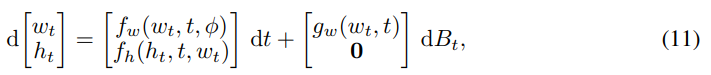 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">為了讓網絡擬合數據,該研究最大化由無限維 ELBO 給出的邊緣似然(marginal likelihood)的下限:
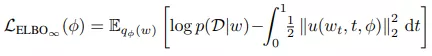 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">采樣權重、隱藏激活函數和訓練目標都是通過一次調用自適應 SDE 求解器同時計算的。
減小方差的梯度估計
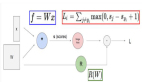
該研究使用 STL(sticking the landing) 估計器來替換 path 空間 KL 中的原始估計器以適應 SDE 設置:
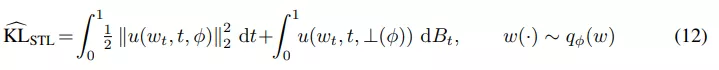 無限深度貝葉斯神經網絡">
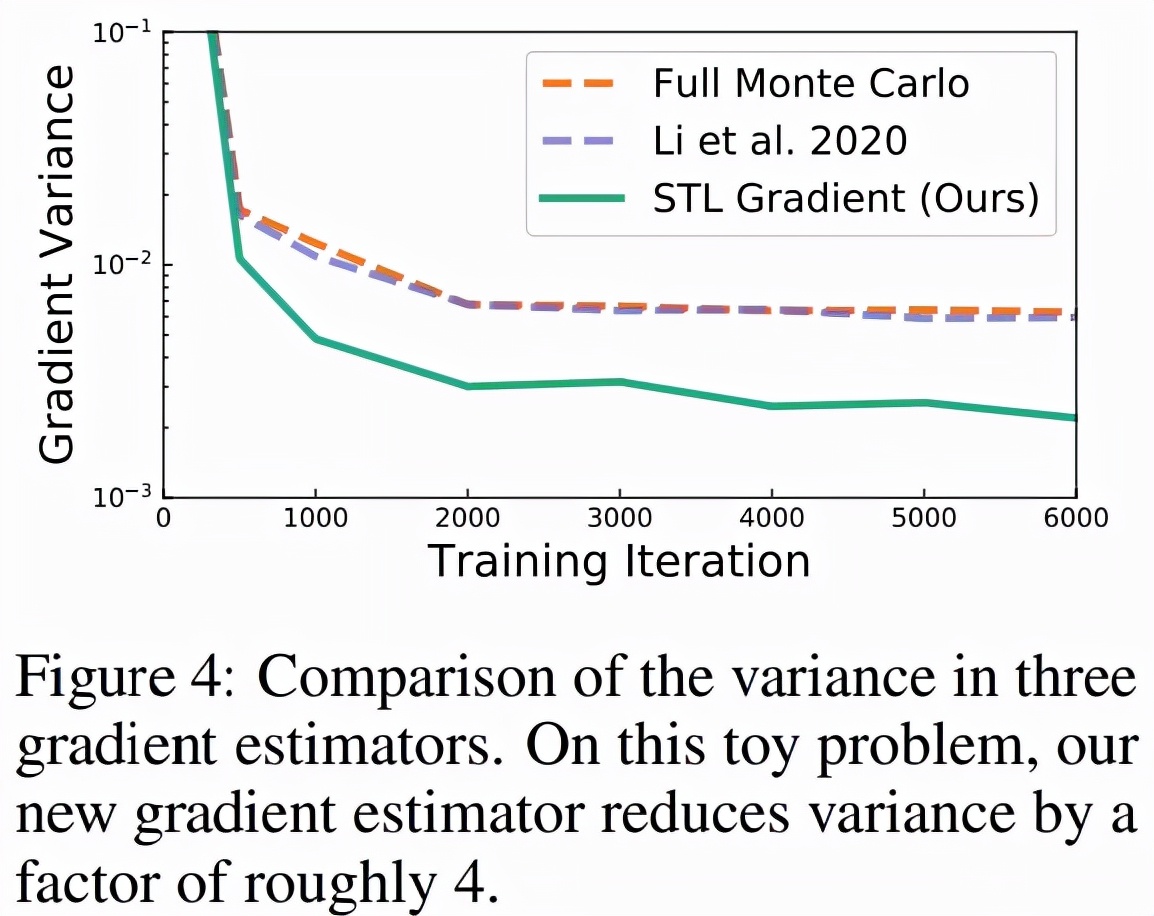
無限深度貝葉斯神經網絡">等式 (12) 中的第二項是鞅(martingale),期望值為零。在之前的工作中,研究者僅對第一項進行了蒙特卡羅估計,但該研究發現這種方法不一定會減少梯度的方差,如下圖 4 所示。
 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">因為該研究提出的近似后驗可以任意表達,研究者推測如果參數化網絡 f_w 的表達能力足夠強,該方法可在訓練結束時實現任意低的梯度方差。
圖 4 顯示了多個梯度估計器的方差,該研究將 STL 與「完全蒙特卡羅(Full Monte Carlo)」估計進行了比較。圖 4 顯示,當匹配指數布朗運動時,STL 獲得的方差比其他方案低。下表 4 顯示了訓練性能的改進。
 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">實驗
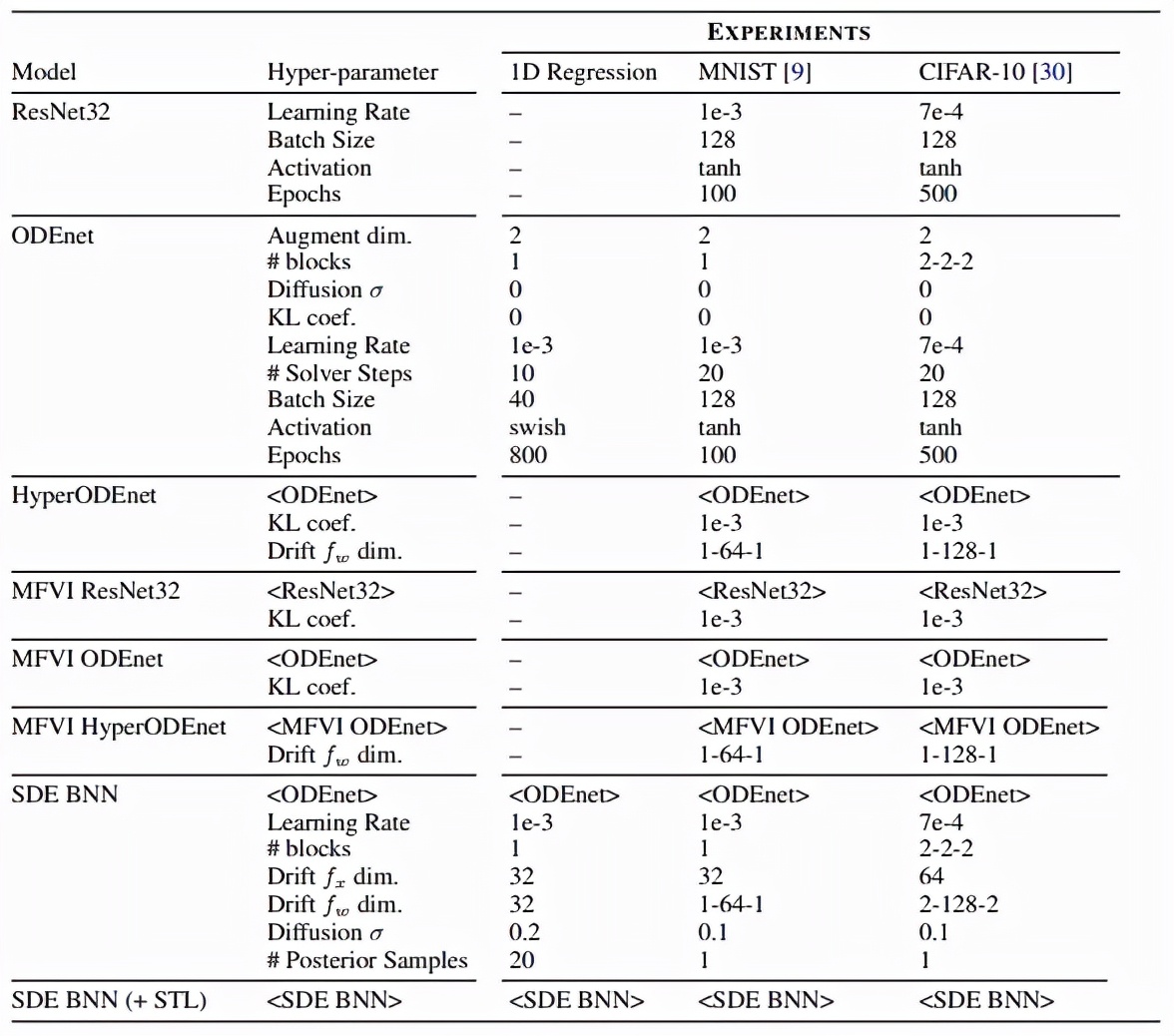
該研究的實驗設置如下表所示,該研究在 MNIST 和 CIFAR-10 上進行了 toy 回歸、圖像分類任務,此外他們還研究了分布外泛化任務:
 無限深度貝葉斯神經網絡">
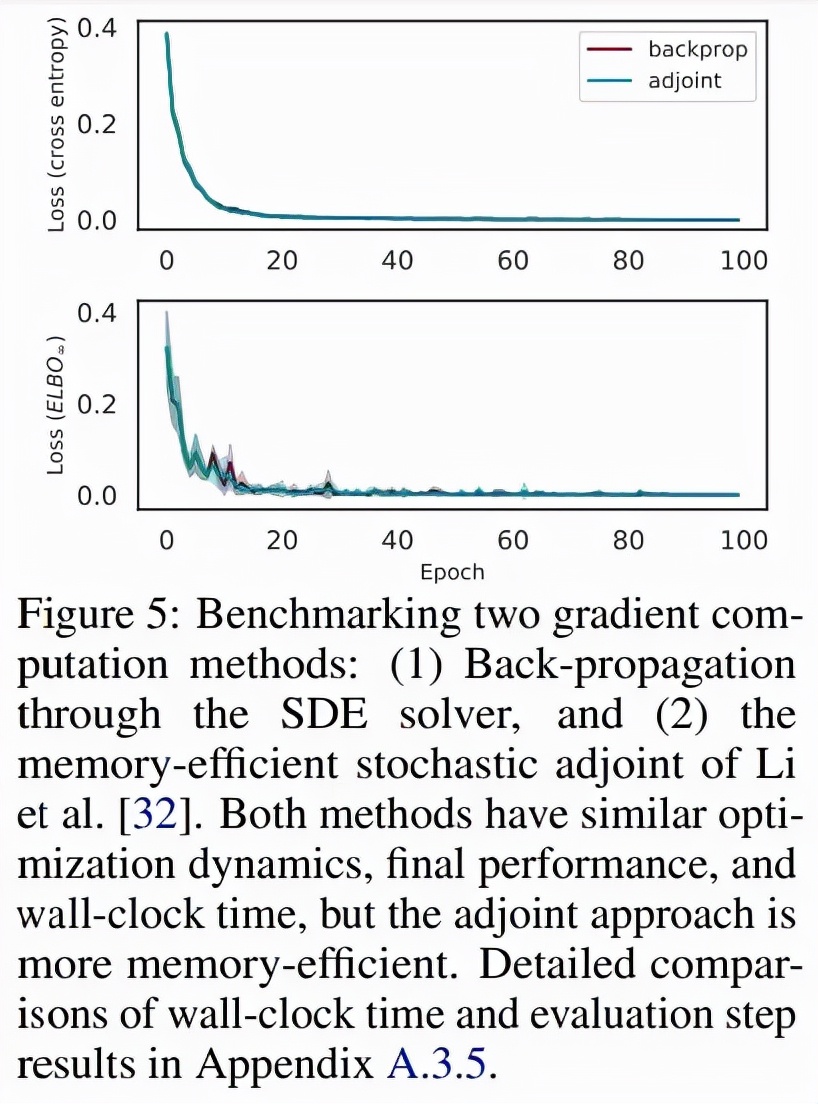
無限深度貝葉斯神經網絡">為了對比求解器與 adjoint 的反向傳播,研究者比較了固定和自適應步長的 SDE 求解器,并比較了 Li 等人提出的隨機 adjoint 之間的比較, 圖 5 顯示了這兩種方法具有相似的收斂性:
 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">1D 回歸
該研究首先驗證了 SDE-BNN 在 1D 回歸問題上的表現。以彌散過程的樣本為條件,來自 1D SDE-BNN 的每個樣本都是從輸入到輸出的雙向映射。這意味著從 1D SDE-BNN 采樣的每個函數都是單調的。為了能夠對非單調函數進行采樣,該研究使用初始化為零的 2 個額外維度來增加狀態。圖 2 顯示了模型在合成的非單調 1D 數據集上學習了相當靈活的近似后驗。
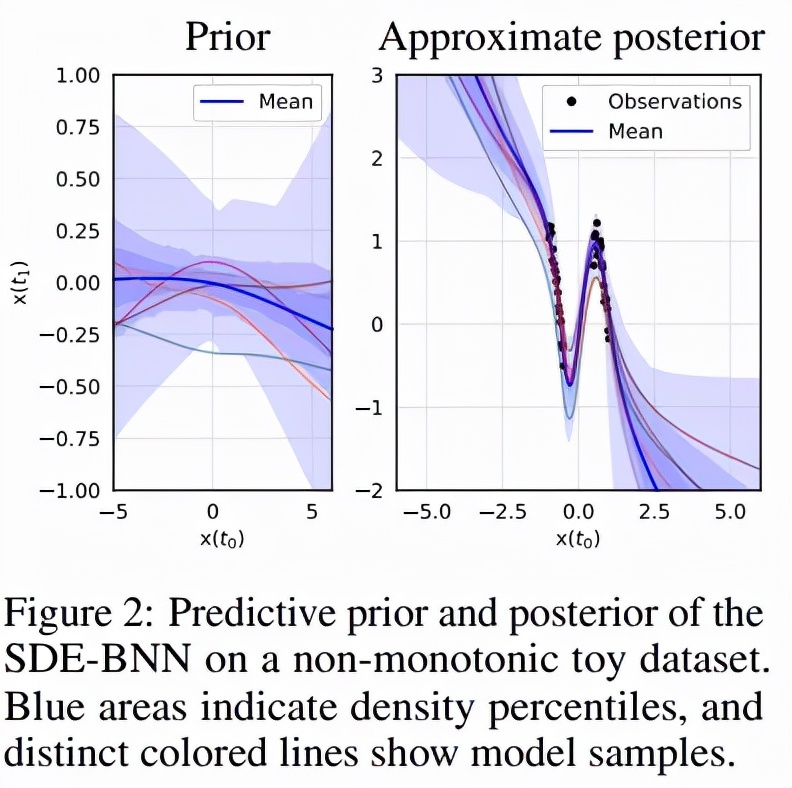 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">圖像分類
表 1 給出了圖像分類實驗的結果。SDE-BNN 通常優于基線,由結果可得雖然連續深度神經 ODE (ODEnet) 模型可以在標準殘差網絡上實現類似的分類性能,但校準(calibration)較差。
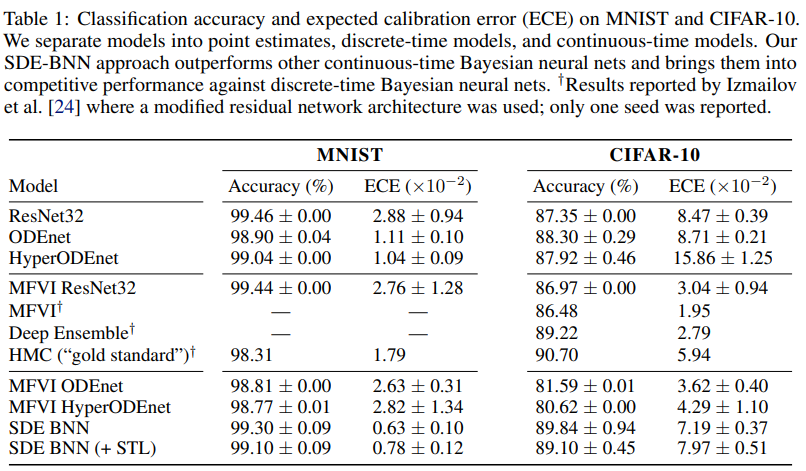 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">圖 6a 展示了 SDE-BNN 的性能,圖 6b 顯示具有相似準確率但比神經 ODE 校準更好的結果。
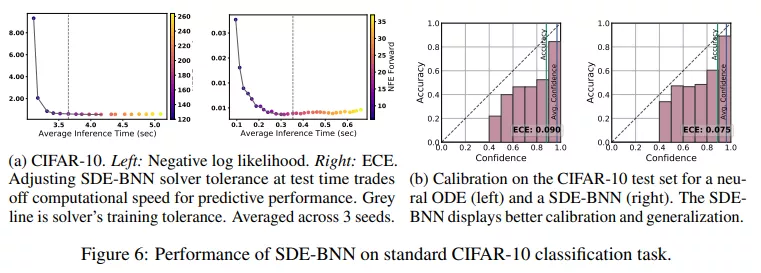 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">表 1 用預期校準誤差量化了模型的校準。SDE-BNN 似乎比神經 ODE 和平均場 ResNet 基線能更好地校準。
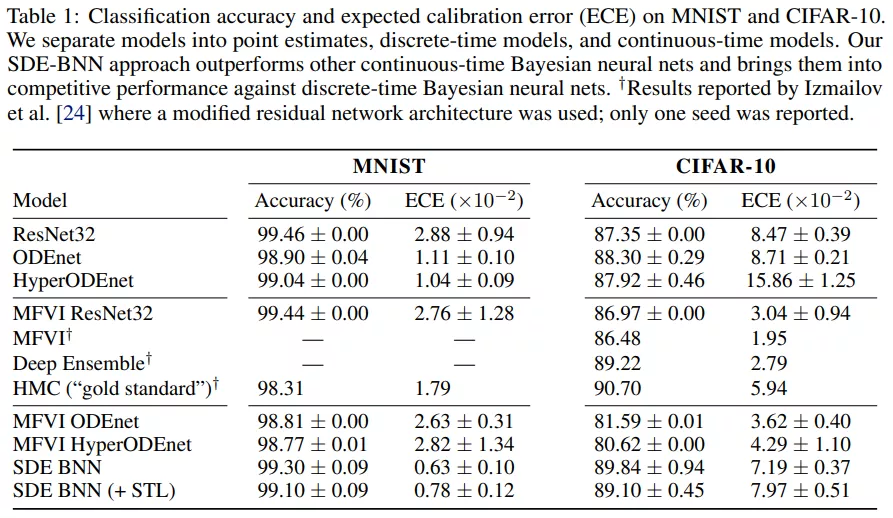 無限深度貝葉斯神經網絡">
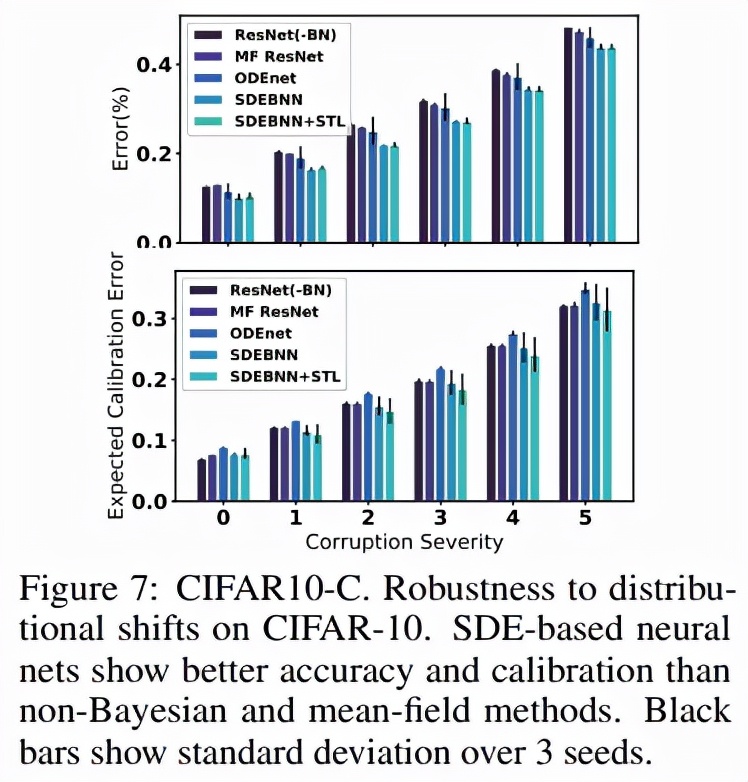
無限深度貝葉斯神經網絡">下圖 7 顯示了損壞測試集上相對于未損壞數據的誤差,表明隨著擾動嚴重性級別的增加以及表 1 中總結的總體誤差度量,mCE 穩步增加。在 CIFAR10 和 CIFAR10-C 上,SDE-BNN 和 SDE -BNN + STL 模型實現了比基線更低的整體測試誤差和更好的校準。
 無限深度貝葉斯神經網絡">
無限深度貝葉斯神經網絡">與標準基線(ResNet32 和 MF ResNet32)相比,SDE-BNN 的絕對損壞誤差(CE)降低了約 4.4%。域外輸入的學習不確定性的有效性表明,盡管沒有在多種形式的損壞上進行訓練,但 SDE-BNN 對觀測擾動也更加穩健。