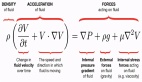
偏微分方程有了基礎模型:樣本需求數(shù)量級減少,14項任務表現(xiàn)最佳
偏微分方程(PDEs)被稱為物理學的語言,因為它們可以在廣泛的時間 - 空間尺度上對各種各樣的物理現(xiàn)象進行數(shù)學建模。常用的有限差分、有限元等數(shù)值方法通常用于近似或模擬偏微分方程。
然而,這些方法計算成本高昂,特別是對于多查詢問題更是如此,因而人們設計了各種數(shù)據(jù)驅動的機器學習(ML)方法來模擬偏微分方程。其中,算子學習( operator learning)算法近年來受到越來越多的關注。
然而,現(xiàn)有的算子學習方法樣本效率并不高,因為它們需要大量的訓練樣例才能以期望的準確率學習目標解算子(如圖 1 所示)。這阻礙了算子學習的廣泛使用,因為通過數(shù)值模擬或底層物理系統(tǒng)的測量來生成特定任務的訓練數(shù)據(jù)非常昂貴。
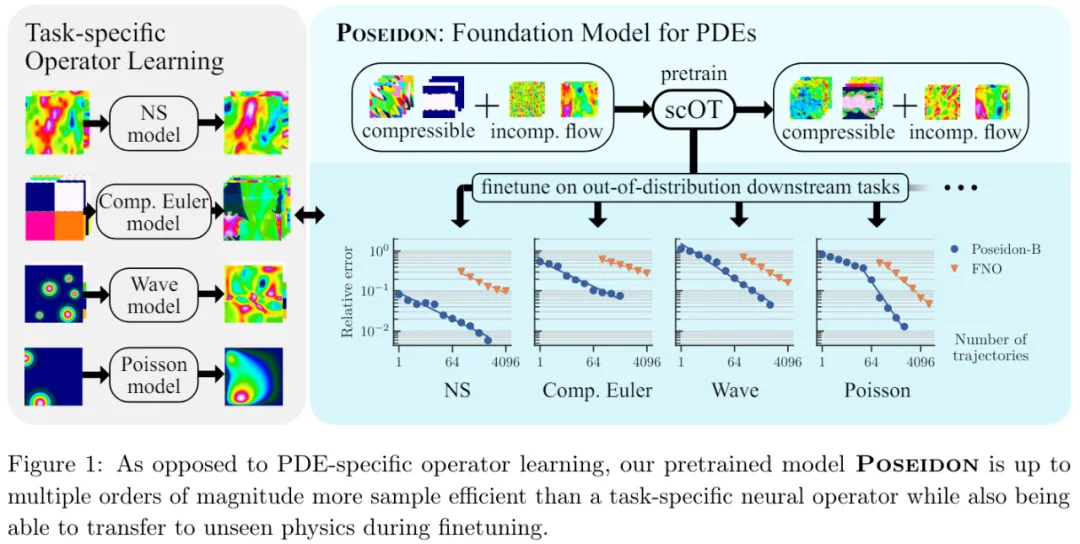
研究者不禁提出,如何才能顯著減少 PDE 學習所需的訓練樣本數(shù)量?
來自蘇黎世聯(lián)邦理工學院等機構的研究者提出了 Poseidon,這是一種用于學習 PDE 解算子的基礎模型。該模型基于多尺度 operator transformer,可實現(xiàn)連續(xù)時間評估。
研究者將 Poseidon 在大規(guī)模數(shù)據(jù)集上進行了預訓練,然后對其進行評估。具體而言,他們在 15 項具有挑戰(zhàn)性的下游任務上對 Poseidon 進行了評估,這些任務涵蓋線性和非線性、時間相關以及橢圓、拋物線、雙曲線和混合型 PDE。
結果表明,Poseidon 在樣本效率和準確率方面都遠遠超過基線,展現(xiàn)出優(yōu)異的性能。
Poseidon 還可以很好地泛化到預訓練期間未見過的物理學問題。此外,Poseidon 可以根據(jù)模型和數(shù)據(jù)大小進行擴展,無論是預訓練還是下游任務。總結來看,本文展示了 Poseidon 的驚人能力,它能夠在預訓練期間從非常小的一組 PDE 中學習有效表示,從而很好地擴展到下游未見過和不相關的 PDE,證明了其作為有效通用 PDE 基礎模型的潛力。
這些結果首次肯定了 PDE 基礎模型的可行性這一基本問題,并為進一步開發(fā)和部署 Poseidon 作為高效的通用 PDE 基礎模型鋪平了道路。
最后,Poseidon 模型以及底層預訓練和下游數(shù)據(jù)集都是開源的。

- 論文地址:https://arxiv.org/pdf/2405.19101
- 項目地址:https://github.com/camlab-ethz/poseidon
- 論文標題:Poseidon: Efficient Foundation Models for PDEs
方法介紹
問題描述:該研究將偏微分方程表示為:
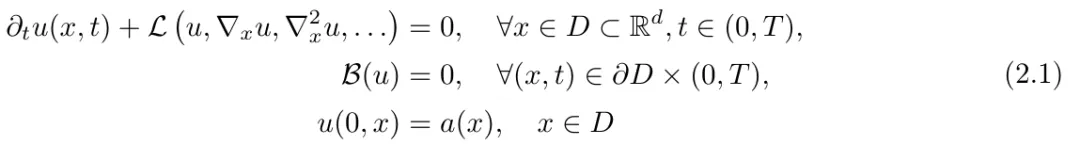
然后假設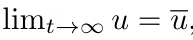 ,可以得到與時間無關的 PDE 的解:
,可以得到與時間無關的 PDE 的解:
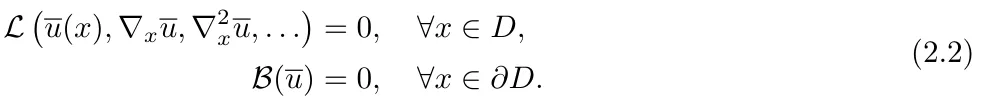
模型架構。Poseidon(圖 1 和圖 2)包括:i)可擴展的 Operator Transformer 或 scOT,這是一種具有(移位)窗口或 Swin 注意力機制的多尺度視覺 transformer,適用于算子學習;ii)一種新穎的 all2all 訓練策略;iii)以及一個開源大型預訓練數(shù)據(jù)集。
其中 scOT 是一種具有前置時間條件的分層多尺度視覺 transformer,用來處理前置時間 t 和函數(shù)空間值初始數(shù)據(jù)輸入 a,以近似 PDE (2.1) 的解算子 S (t, a)。
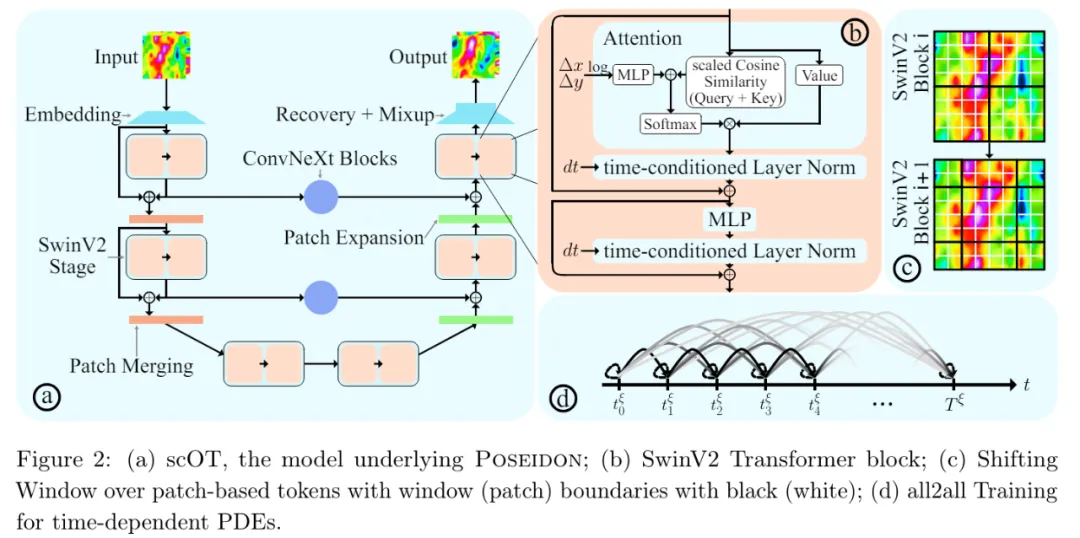
接著如圖 2 (a) 所示,研究者通過 SwinV2 transformer 塊對 patch 嵌入的輸出進行處理,每個 transformer 塊的結構表示為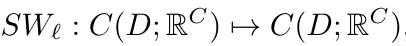 ,得到:
,得到:
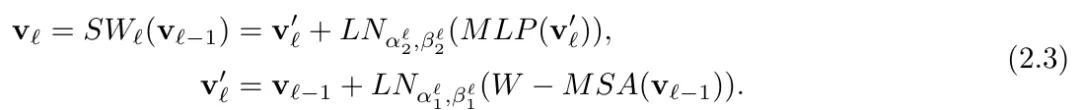
通過在 (2.3) 中引入前置時間條件層范數(shù),該研究提出了一種時間調(diào)節(jié)策略。
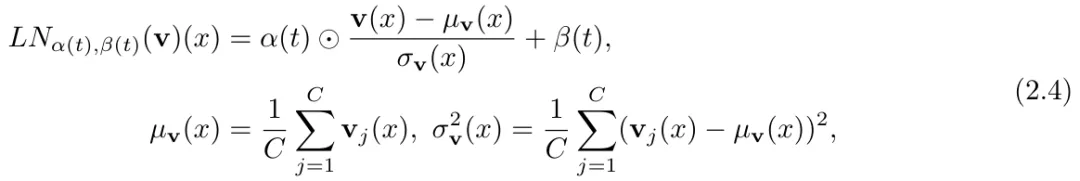
最后,如圖 2 (a) 所示,SwinV2 transformer 塊在 U-Net 類型的編碼器 - 解碼器架構中以層級多尺度方式排列,通過使用 patch 合并(下采樣)和 patch 擴展(上采樣)操作完成。
實驗結果
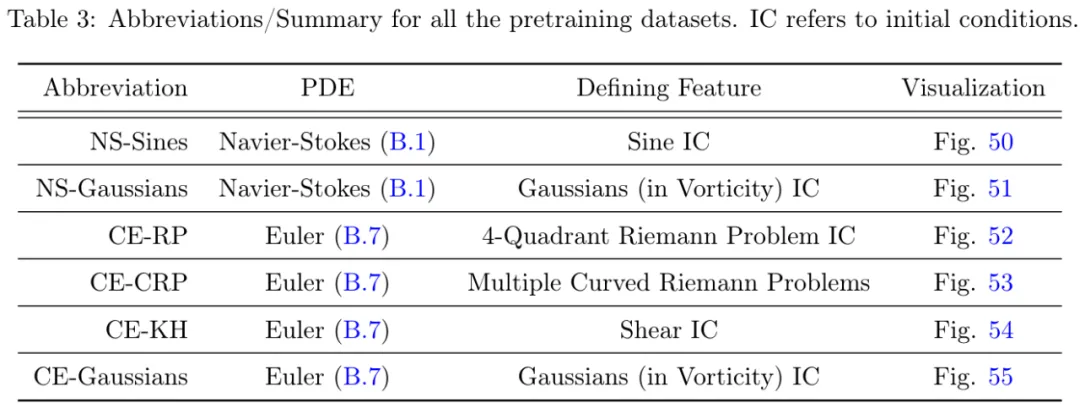
預訓練數(shù)據(jù):研究者提供了包含 6 個算子的數(shù)據(jù)集,詳細信息如下所示。
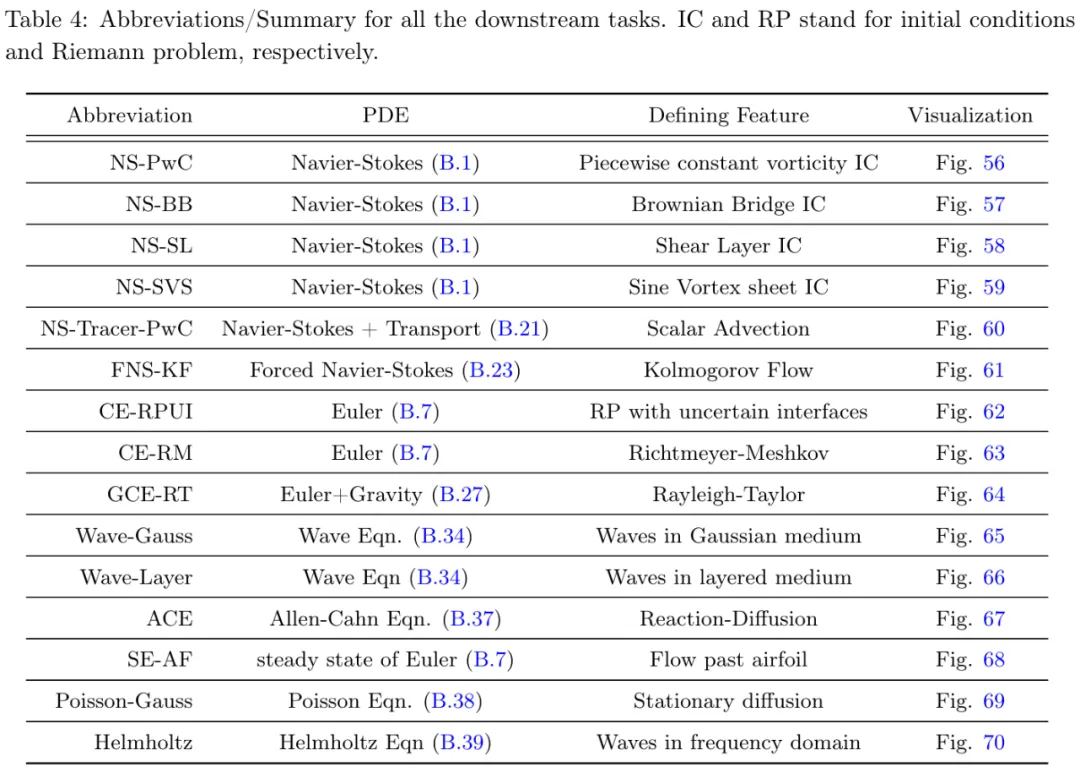
下游任務:研究者在 15 個具有挑戰(zhàn)性的下游任務上進行了實驗,如表 4 所示。
模型:本文考慮了三種不同的 Poseidon 模型:i) Poseidon-T ≈ 21M 個參數(shù),ii) Poseidon-B ≈ 158M 個參數(shù),iii) Poseidon-L ≈ 629M 個參數(shù)。
實驗結果顯示,Poseidon 在 15 個下游任務中都表現(xiàn)良好,明顯優(yōu)于 FNO( Fourier Neural Operator )(參考論文中的圖 7 - 圖 21,這里只展示圖 7 )。
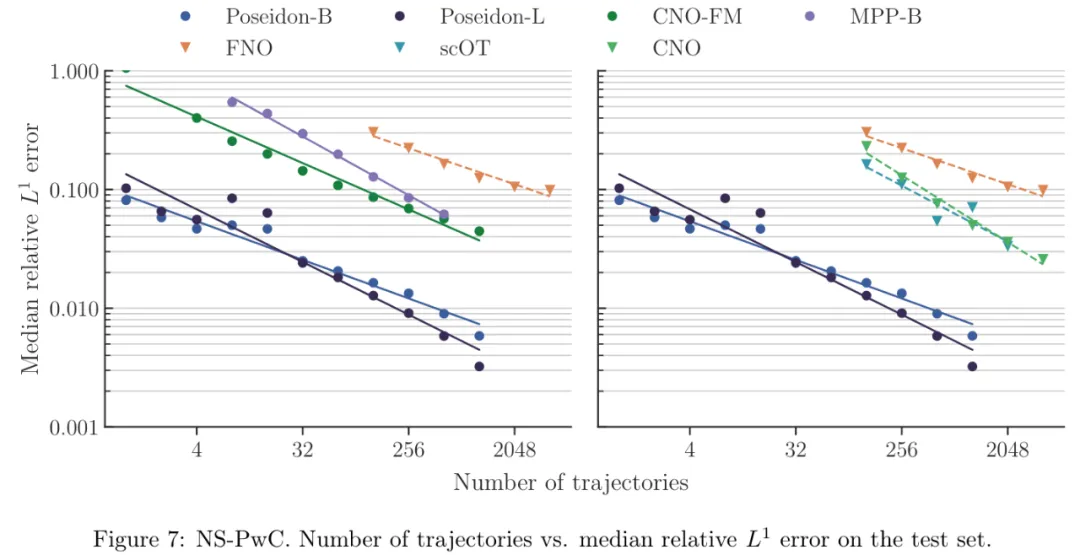
表 1 進一步支持了這一點。
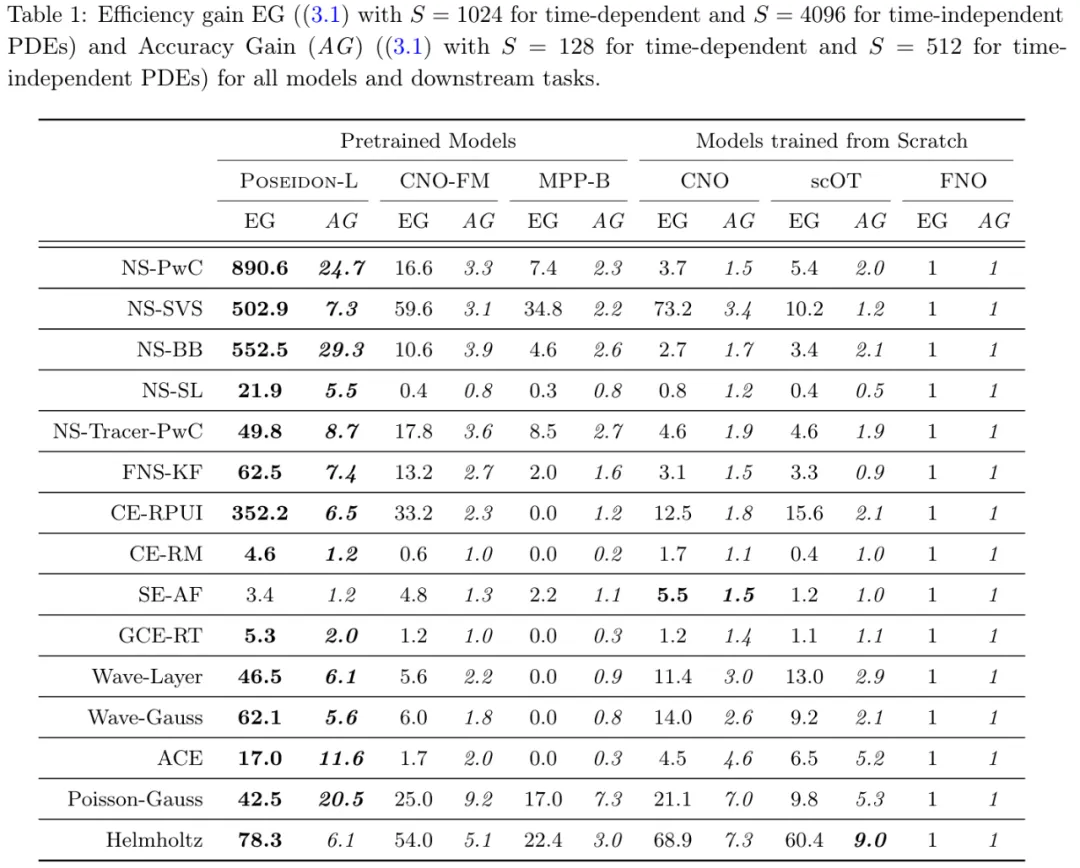
從表 9 可得,平均而言,Poseidon-L 僅需要 20 個樣本即可達到 FNO 的 1024 個樣本的誤差,并且在 13 個(15 個)任務中,Poseidon-L 所需的樣本比 FNO 少一個數(shù)量級。同樣,從表 1 和表 9 中可以看到,對于相同數(shù)量的樣本,Poseidon-L 的誤差明顯低于 FNO,增益范圍從 10% 到 25 倍不等 ,此外,Poseidon 可以很好地泛化到未見過的物理任務。
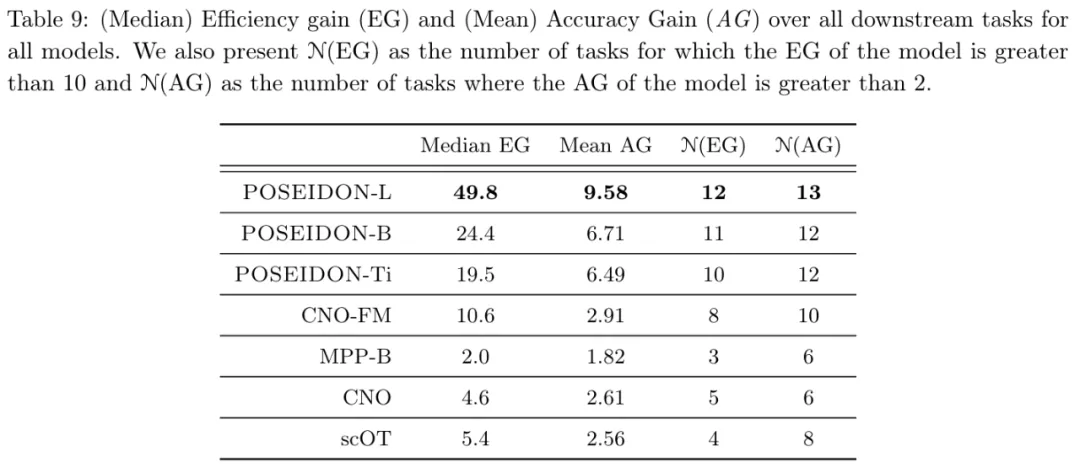
從表 1 和表 9 可以觀察到,在 15 項下游任務中,Poseidon 在 14 項上的表現(xiàn)明顯優(yōu)于 CNO-FM。平均而言,CNO-FM 需要大約 100 個特定于任務的示例才能達到 FNO 的 1024 個樣本的誤差水平,而 Poseidon 只需要大約 20 個。由于 CNO-FM 和 Poseidon 已在完全相同的數(shù)據(jù)集上進行了預訓練,因此這種性能差異很大程度上可以歸因于架構差異,因為 CNO-FM 基于多尺度 CNN,而 Poseidon 的主干則是多尺度視覺 transformer。
從圖 22 可以看出,隨著 Poseidon 模型大小的增加,預訓練數(shù)據(jù)集上的訓練和評估(驗證)錯誤都明顯減少。
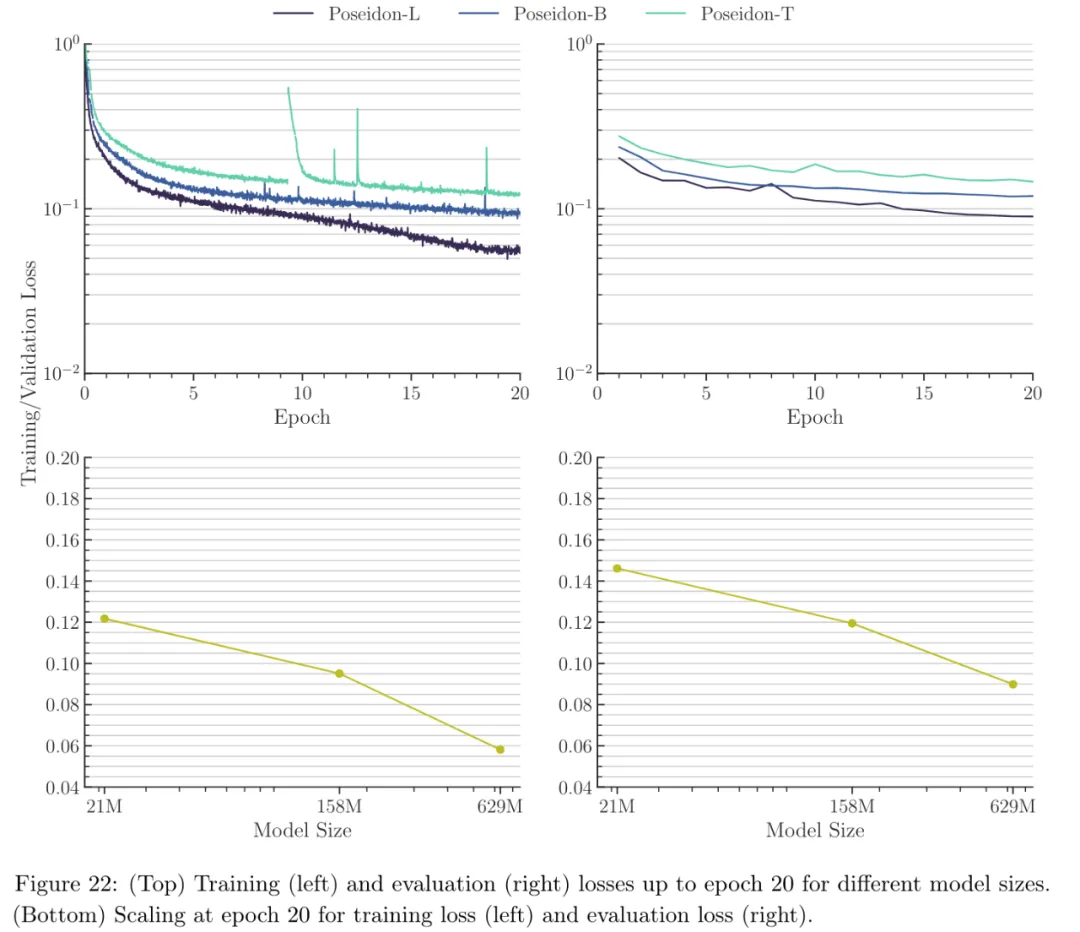
了解更多結果,請參考原論文。