用定租問題學透K近鄰算法
k近鄰思想是我覺得最純粹最清晰的一個思想,k近鄰算法(KNN)只是這個思想在數據領域都一個應用。
你的工資由你周圍的人決定。
你的水平由你身邊最接近的人的水平決定。
你所看到的世界,由你身邊的人決定。
思想歸思想,不能被編碼那也無法應用于數據科學領域。
我們提出問題,然后應用該方法加以解決,以此加深我們對方法的理解。
問題: 假設你是airbnb平臺的房東,怎么給自己的房子定租金呢?
分析: 租客根據airbnb平臺上的租房信息,主要包括價格、臥室數量、房屋類型、位置等等挑選自己滿意的房子。給房子定租金是跟市場動態息息相關的,同樣類型的房子我們收費太高租客肯定不租,收費太低收益又不好。
解答: 收集跟我們房子條件差不多的一些房子信息,確定跟我們房子最相近的幾個,然后求其定價的平均值,以此作為我們房子的租金。
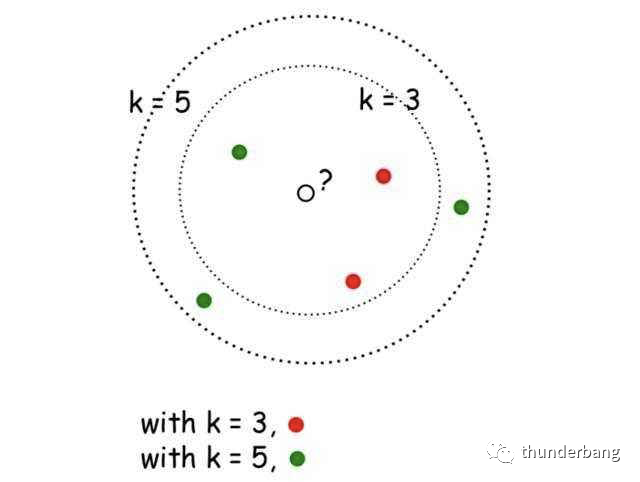
這就是K-Nearest Neighbors(KNN),k近鄰算法。KNN的核心思想是未標記樣本的類別,由距離其最近的k個鄰居投票決定。
本文就基于房租定價問題梳理下該算法應用的全流程,包含如下部分。
- 讀入數據
- 數據處理
- 手寫算法代碼預測
- 利用sklearn作模型預測
- 超參優化
- 交叉驗證
- 總結
提前聲明,本數據集是公開的,你可以在網上找到很多相關主題的材料,本文力圖解釋地完整且精準,如果你找到了更詳實的學習材料,那再好不過了。
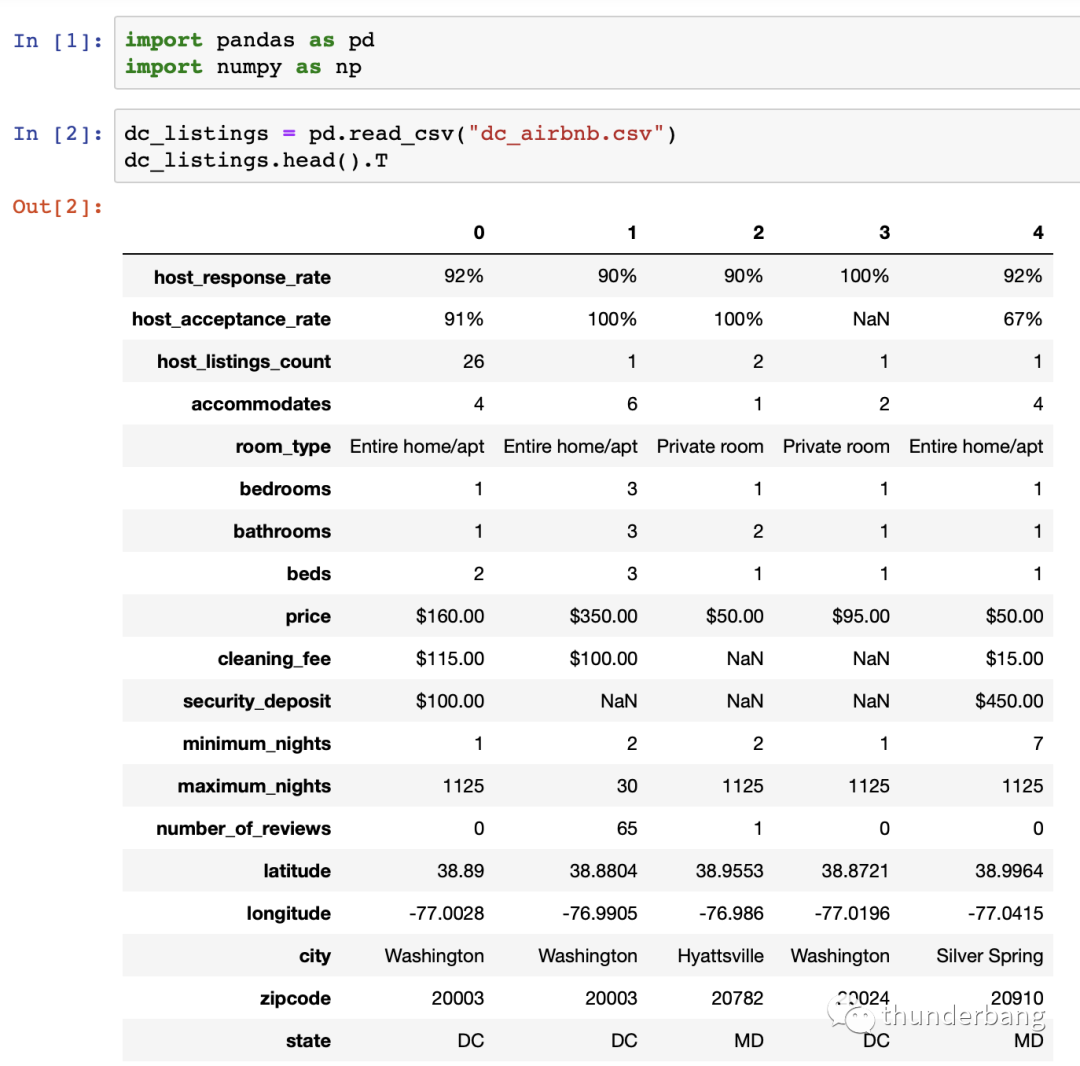
1.讀入數據
先讀入數據,了解下數據情況,發現目標變量price,以及cleaning_fee和security_deposit的格式有點問題,另有一些變量是字符型,都需要處理。我對dataframe進行了轉置顯示,方便查看。
2.數據處理
我們先只處理price,盡量集中在算法思想本身上面去。
- # 處理下目標變量price,并轉換成數值型
- stripped_commas = dc_listings['price'].str.replace(',', '')
- stripped_dollars = stripped_commas.str.replace('$', '')
- dc_listings['price'] = stripped_dollars.astype('float')
- # k近鄰算法也是模型,需要劃分訓練集和測試集
- sample_num = len(dc_listings)
- # 在這我們先把數據隨機打散,保證數據集的切分隨機有效
- dc_listings = dc_listings.loc[np.random.permutation(len(sample_num))]
- train_df = dc_listings.iloc[0:int(0.7*sample_num)]
- test_df = dc_listings.iloc[int(0.7*sample_num):]
3.手寫算法代碼預測
根據k近鄰算法的定義直接編寫代碼,從簡單高效上考慮,我們僅針對單變量作預測。
入住人數應該是和租金關聯度很高的信息,面積應該也是。我們這里采用前者。
我們的目標是理解算法邏輯。實際操作中一般不會只考慮單一變量。
- # 注意,這兒是train_df
- def predict_price(new_listing):
- temp_df = train_df.copy()
- temp_df['distance'] = temp_df['accommodates'].apply(lambda x: np.abs(x - new_listing))
- temp_df = temp_df.sort_values('distance')
- nearest_neighbor_prices = temp_df.iloc[0:5]['price']
- predicted_price = nearest_neighbor_prices.mean()
- return(predicted_price)
- # 這兒是test_df
- test_df['predicted_price'] = test_df['accommodates'].apply(predict_price)
- # MAE(mean absolute error), MSE(mean squared error), RMSE(root mean squared error)
- test_df['squared_error'] = (test_df['predicted_price'] - test_df['price'])**(2)
- mse = test_df['squared_error'].mean()
- rmse = mse ** (1/2)
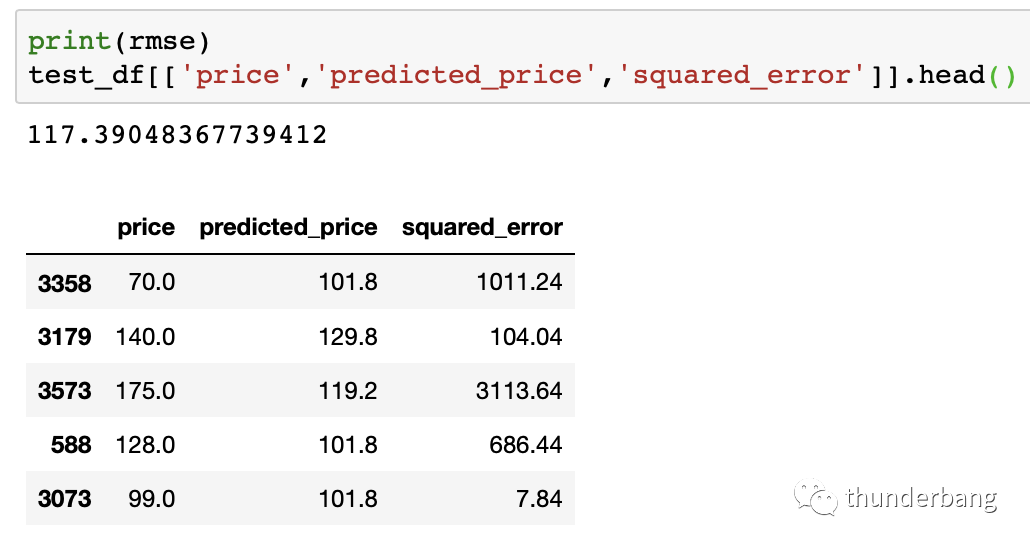
值得強調的是,模型算法的構建都是基于訓練集的,預測評估基于測試集。應用評估嚴格上還有一類樣本,oot:跨時間樣本。
從結果來看,即使我們只用了入住人數accommodates這一個變量去做近鄰選擇,預測結果也是很有效的。
4.利用sklearn作模型預測
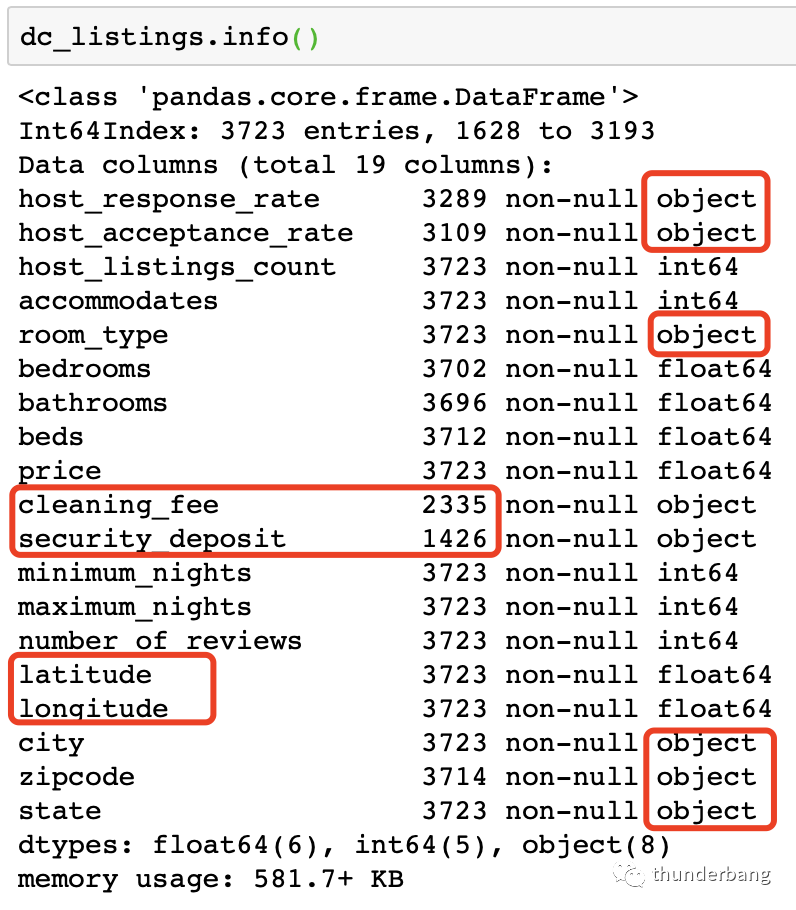
這次我們要用更多的變量,只剔掉字符串和不可解釋的變量,剩下能用的變量都用上。
當用了多個變量的時候,這些不變量綱是不一樣的,我們需要進行標準化處理。保證了各自變量的分布差異,同時又保證變量之間可疊加。
- # 剔掉非數值型變量和不合適的變量
- drop_columns = ['room_type', 'city', 'state', 'latitude', 'longitude', 'zipcode', 'host_response_rate', 'host_acceptance_rate', 'host_listings_count']
- dc_listings = dc_listings.drop(drop_columns, axis=1)
- # 剔掉缺失比例過高的列(變量)
- dc_listings = dc_listings.drop(['cleaning_fee', 'security_deposit'], axis=1)
- # 剔掉有缺失值的行(樣本)
- dc_listings = dc_listings.dropna(axis=0)
- # 多個變量的量綱不一樣,需要標準化
- normalized_listings = (dc_listings - dc_listings.mean())/(dc_listings.std())
- normalized_listings['price'] = dc_listings['price']
- # 于是我們得到了可用于建模的數據集,7:3劃分訓練集測試集
- train_df = normalized_listings.iloc[0:int(0.7*len(normalized_listings))]
- test_df = normalized_listings.iloc[int(0.7*len(normalized_listings)):]
- # price是y,其余變量都是X
- features = train_df.columns.tolist()
- features.remove('price')
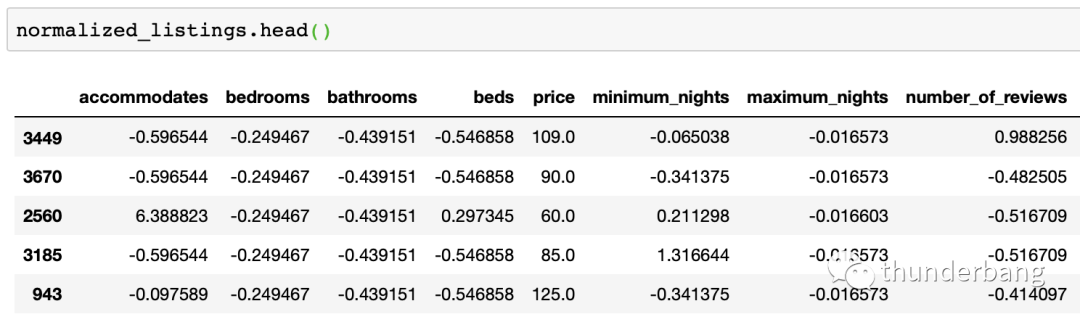
處理后的數據集如下,其中price是我們要預測的目標,其余是可用的變量。
- from sklearn.neighbors import KNeighborsRegressor
- from sklearn.metrics import mean_squared_error
- knn = KNeighborsRegressor(n_neighbors=5, algorithm='brute')
- knn.fit(train_df[features], train_df['price'])
- predictions = knn.predict(test_df[features])
- mse = mean_squared_error(test_df['price'], predictions)
- rmse = mse ** (1/2)
最后得到的rmse=111.9,相比單變量knn的117.4要小,結果得到優化。嚴格來說,這個對比不完全公平,因為我們丟掉了少量的特征缺失樣本。
5.超參優化
在第3和第4部分,我們預設了k=5,但這個拍腦袋確定的。該取值合不合理,是不是最優,都需要進一步確定。
其中,這個k就是一個超參數。對于任何一個數據集,只要你用knn,就需要確定這個k值。
k值不是通過模型基于數據去學習得到的,而是通過預設,然后根據結果反選確定的。任何一個超參數都是這樣確定的,其他算法也如此。
- import matplotlib.pyplot as plt
- %matplotlib inline
- hyper_params = [x for x in range(1,21)]
- rmse_values = []
- features = train_df.columns.tolist()
- features.remove('price')
- for hp in hyper_params:
- knn = KNeighborsRegressor(n_neighbors=hp, algorithm='brute')
- knn.fit(train_df[features], train_df['price'])
- predictions = knn.predict(test_df[features])
- mse = mean_squared_error(test_df['price'], predictions)
- rmse = mse**(1/2)
- rmse_values.append(rmse)
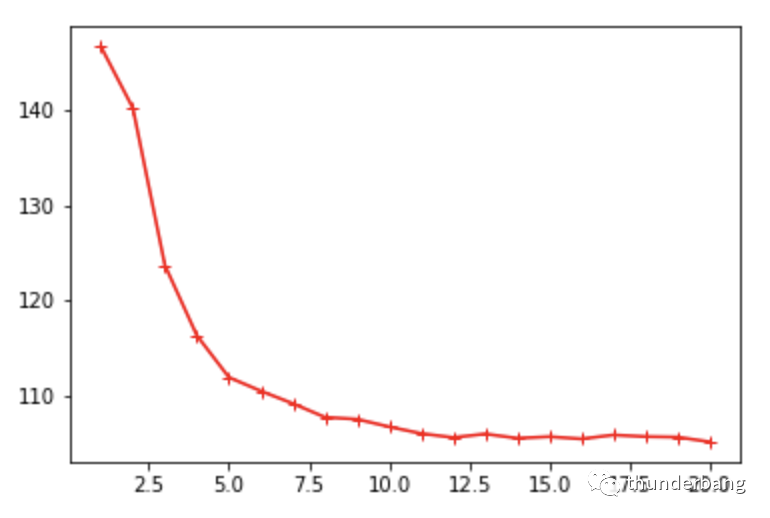
- plt.plot(hyper_params, rmse_values,c='r',linestyle='-',marker='+')
我們發現,k越大,預測價格和真實價格的偏差從趨勢看會更準確。但要注意,k越大計算量就越大。
我們在確定k值時,可以用albow法,也就是看上圖的拐點,形象上就是手肘的肘部。
相比k=5,k=7或10可能是更好的結果。
6.交叉驗證
上面我們的計算結果完全依賴訓練集和測試集,雖然對它們的劃分我們已經考慮了隨機性。但一次結果仍然具備偶爾性,尤其是當樣本量不夠大時。
交叉驗證就是為了解決這個問題。我們可以對同一個樣本集進行不同的訓練集測試集劃分。每次劃分后都重新進行訓練和預測,然后綜合去看待這些結果。
應用最廣泛的是n折交叉驗證,其過程是隨機將數據集切分成n份,用其中n-1個子集做訓練集,剩余1個子集做測試集。這樣一共可以進行n次訓練和預測。
我們可以直接手寫該邏輯,如下。
- sample_num = len(normalized_listings)
- normalized_listings.loc[normalized_listings.index[0:int(0.2*sample_num)], "fold"] = 1
- normalized_listings.loc[normalized_listings.index[int(0.2*sample_num):int(0.4*sample_num)], "fold"] = 2
- normalized_listings.loc[normalized_listings.index[int(0.4*sample_num):int(0.6*sample_num)], "fold"] = 3
- normalized_listings.loc[normalized_listings.index[int(0.6*sample_num):int(0.8*sample_num)], "fold"] = 4
- normalized_listings.loc[normalized_listings.index[int(0.8*sample_num):], "fold"] = 5
- fold_ids = [1,2,3,4,5]
- def train_and_validate(df, folds):
- fold_rmses = []
- for fold in folds:
- # Train
- model = KNeighborsRegressor()
- train = df[df["fold"] != fold]
- test = df[df["fold"] == fold].copy()
- model.fit(train[features], train["price"])
- # Predict
- labels = model.predict(test[features])
- test["predicted_price"] = labels
- mse = mean_squared_error(test["price"], test["predicted_price"])
- rmse = mse**(1/2)
- fold_rmses.append(rmse)
- return(fold_rmses)
- rmses = train_and_validate(normalized_listings, fold_ids)
- avg_rmse = np.mean(rmses)
工程上,我們要充分利用工具和資源。sklearn庫就包含了我們常用的機器學習算法實現,可以直接用來驗證。
- from sklearn.model_selection import cross_val_score, KFold
- kf = KFold(5, shuffle=True, random_state=1)
- model = KNeighborsRegressor()
- mses = cross_val_score(model, normalized_listings[features], normalized_listings["price"], scoring="neg_mean_squared_error", cv=kf)
- rmses = np.sqrt(np.absolute(mses))
- avg_rmse = np.mean(rmses)
交叉驗證的結果置信度會更高,尤其是在小數據集上。因為它能夠一定程度地減輕偶然性誤差。
結合交叉驗證和超參優化,我們一般就得到了該數據集下用knn算法預測的最優結果。
- # 超參優化
- num_folds = [x for x in range(2,50,2)]
- rmse_values = []
- for fold in num_folds:
- kf = KFold(fold, shuffle=True, random_state=1)
- model = KNeighborsRegressor()
- mses = cross_val_score(model, normalized_listings[features], normalized_listings["price"], scoring="neg_mean_squared_error", cv=kf)
- rmses = np.sqrt(np.absolute(mses))
- avg_rmse = np.mean(rmses)
- std_rmse = np.std(rmses)
- rmse_values.append(avg_rmse)
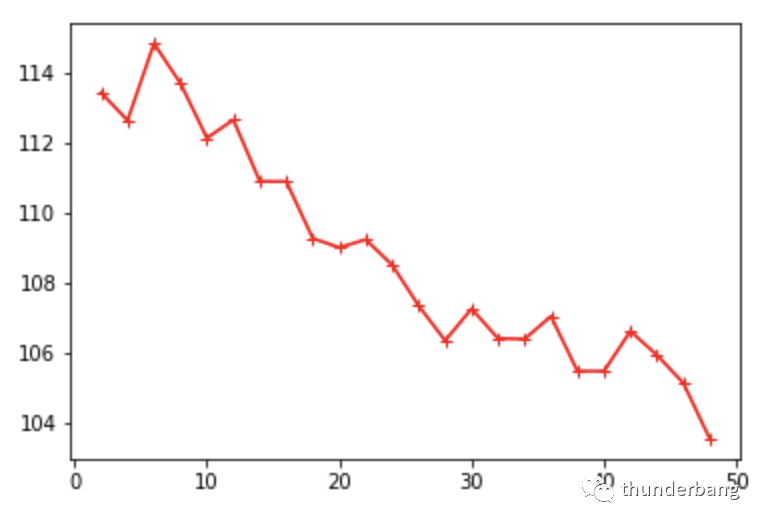
- plt.plot(num_folds, rmse_values,c='r',linestyle='-',marker='+')
我們得到了相同的趨勢,k越大,效果趨勢上更好。同時因為交叉驗證一定程度上解決了過擬合問題,理想的k值越大,模型可以更復雜些。
7.總結
從k-近鄰算法的核心思想以及以上編碼過程可以看出,該算法是基于實例的學習方法,因為它完全依靠訓練集里的實例。
該算法不需什么數學方法,很容易理解。但是非常不適合應用在大數據集上,因為k-近鄰算法每一次預測都需要計算整個訓練集的數據到待預測數據的距離,然后增序排列,計算量巨大。
如果能用數學函數來描述數據集的特征變量與目標變量的關系,那么一旦用訓練集獲得了該函數表示,預測就是簡簡單單的數學計算問題了。計算復雜度大大降低。
其他的經典機器學習算法基本都是一個函數表達問題。后面我們再看。
本文轉載自微信公眾號「 thunderbang」,可以通過以下二維碼關注。轉載本文請聯系 thunderbang公眾號。