譯者 | 朱先忠
審校 | 梁策 孫淑娟
K-最近鄰(K-Nearest Neighbors,KNN)是一種監督學習機器算法,可用于解決機器學習算法中的回歸和分類任務。
KNN可根據當前訓練數據點的特征對測試數據集進行預測。在假設相似的事物在很近的距離內存在的情況下,通過計算測試數據和訓練數據之間的距離來實現這一點。
該算法將學習過的數據存儲起來,使其在預測和分類新數據點時更加有效。當輸入新的數據點時,KNN算法能夠學習該數據的特征。然后,它會把該新的數據點放在那些更接近共享相同特征的當前訓練數據點的位置。
一、KNN中K的含義
通俗來講,KNN中的“K”是一個參數,表示最近鄰的數字。K是一個正整數,通常值很小,建議指定為奇數。K值為數據點創建了一個環境,這樣可以更容易地指定哪個數據點屬于哪個類別。
下面的例子顯示了3個圖表。首先,第一張圖負責完成數據的初始化,其中實現了繪制數據點并把它們歸屬為不同的分類(A與B),并給出了一個待分類的新的樣本。第二張圖負責完成距離的計算。此圖中,計算從新樣本數據點到最近訓練數據點的距離。然而,這仍然沒有完成對新的樣本數據點進行分類。因此,使用K值本質上就是創建了一個鄰域,我們可以在其中對新的樣本數據點進行分類。
于是,我們可以說,當k=3時新數據點將歸屬B類型。因為與A類型相比,有更多訓練過的B類數據點具有與新數據點類似的特征。
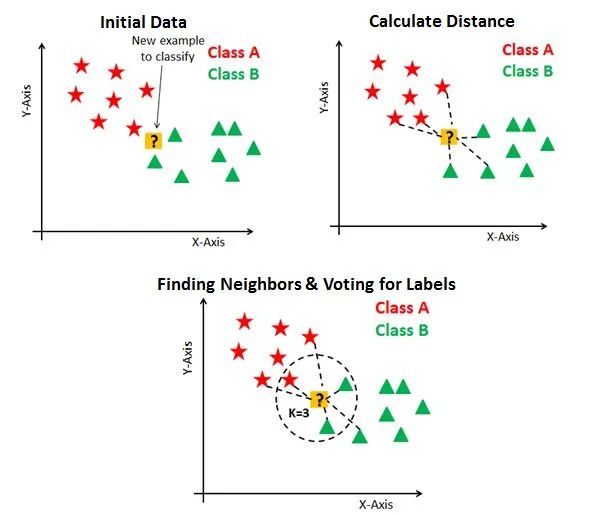
圖表來源:datacamp.com
如果我們將K值增加到7,新數據點將屬于A類型。因為與B類型相比,有更多訓練過的A類型數據點具有與新數據點類似的特征。
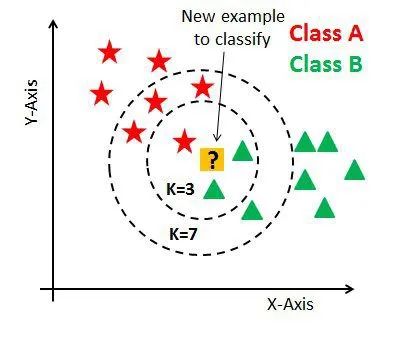
圖表來源:datacamp.com
K值通常是一個小數字,因為隨著K值的增加,錯誤率也會上升。下圖顯示了這一點:
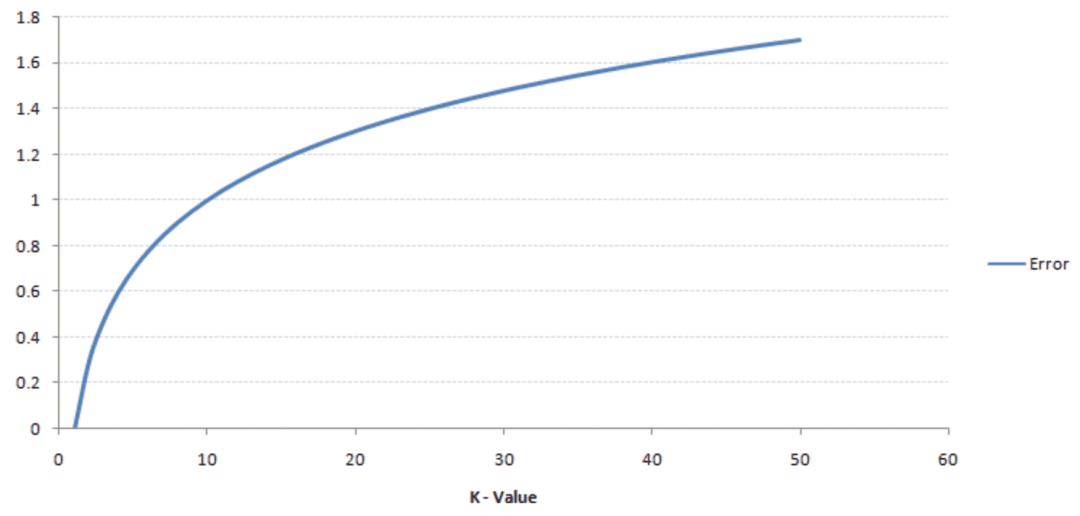
圖表來源:analyticsvidhya
然而,如果K值很小,則會導致低偏差但高方差,從而導致模型過度擬合。
此外,我們還建議把K值指定為奇數。因為如果我們試圖對一個新數據點分類,而我們只有偶數個類型(例如A類型和B類型)的話,則可能會產生不準確的輸出。因此,強烈建議選擇帶有奇數的K值,以避免出現“平局”情況。
二、計算距離
KNN會計算數據點之間的距離,以便對新數據點進行分類。在KNN中計算該距離最常用的方法是歐幾里得法、曼哈頓法和明可夫斯基(Minkowski)法。
歐幾里德距離是使用兩點之間的直線長度來算出兩點間的距離。歐氏距離的公式是新數據點(x)和現有訓練數據點(y)之間的平方差之和的平方根。
曼哈頓距離是兩點之間的距離,是它們笛卡爾坐標絕對差的總和。曼哈頓距離的公式是使用坐標軸上的線段來計算新數據點(x)和現有訓練數據點(y)之間的長度之和。
明可夫斯基距離是賦范向量空間中兩點之間的距離,是歐幾里德距離和曼哈頓距離的推廣。在p=2時的明可夫斯基距離公式中,我們得到了歐幾里得距離,也稱為L2距離。當p=1時,我們得到曼哈頓距離,也稱為L1距離,或者稱城市街區距離,又叫作LASSO距離。
下圖給出了相應的公式:

下圖解釋了三者之間的區別:
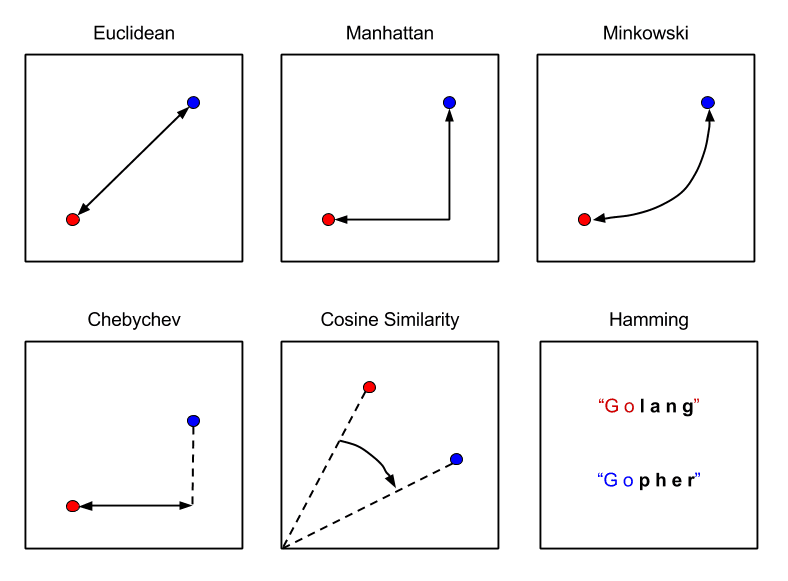
圖表來源:Packt訂閱
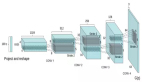
三、KNN算法工作原理
- 以下給出了KNN算法的工作步驟:
- 加載數據集
- 選擇一個K值,建議使用奇數以避免平局情形。
- 計算新數據點與相鄰現有訓練數據點之間的距離。
找到距離新數據點最近的第K個鄰近點。
下圖概述了這些步驟:
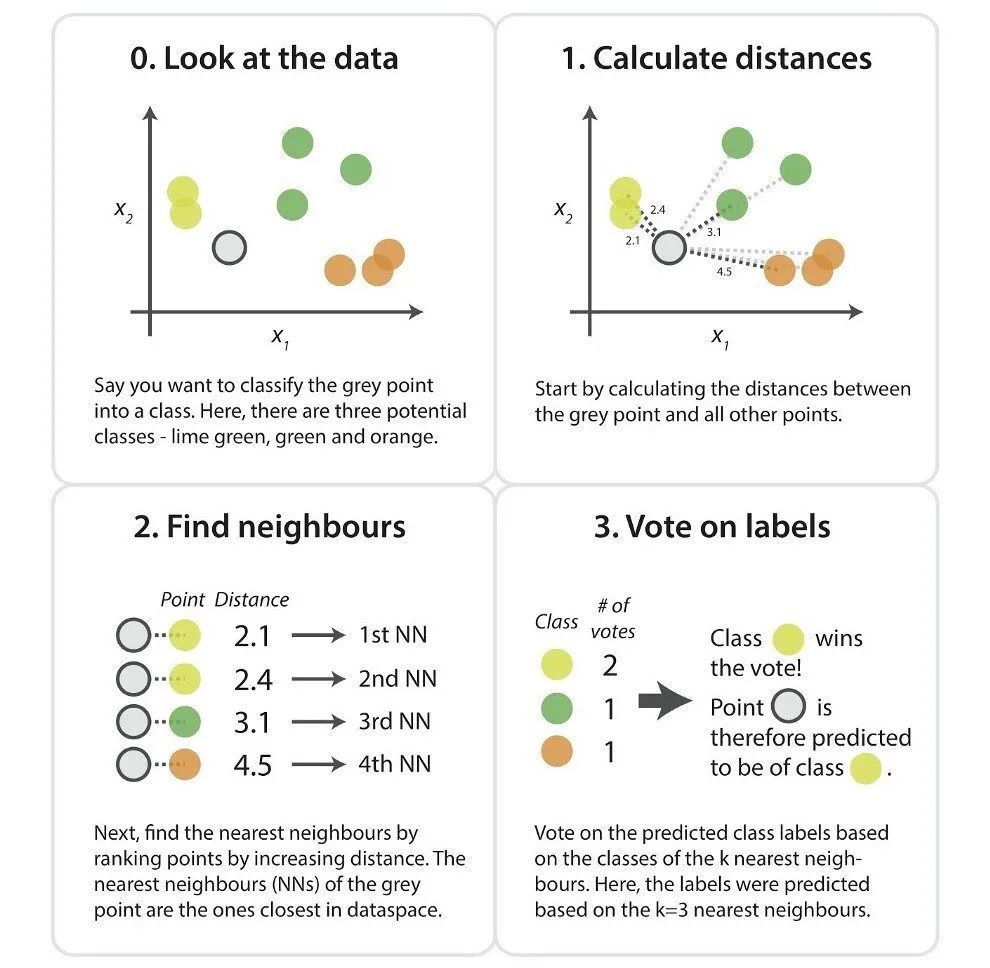
圖表來源:kdnuggets.com
四、KNN算法的分類任務應用舉例
下文是一個借助Iris數據集在分類任務中使用KNN算法的示例:
1.導入庫
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
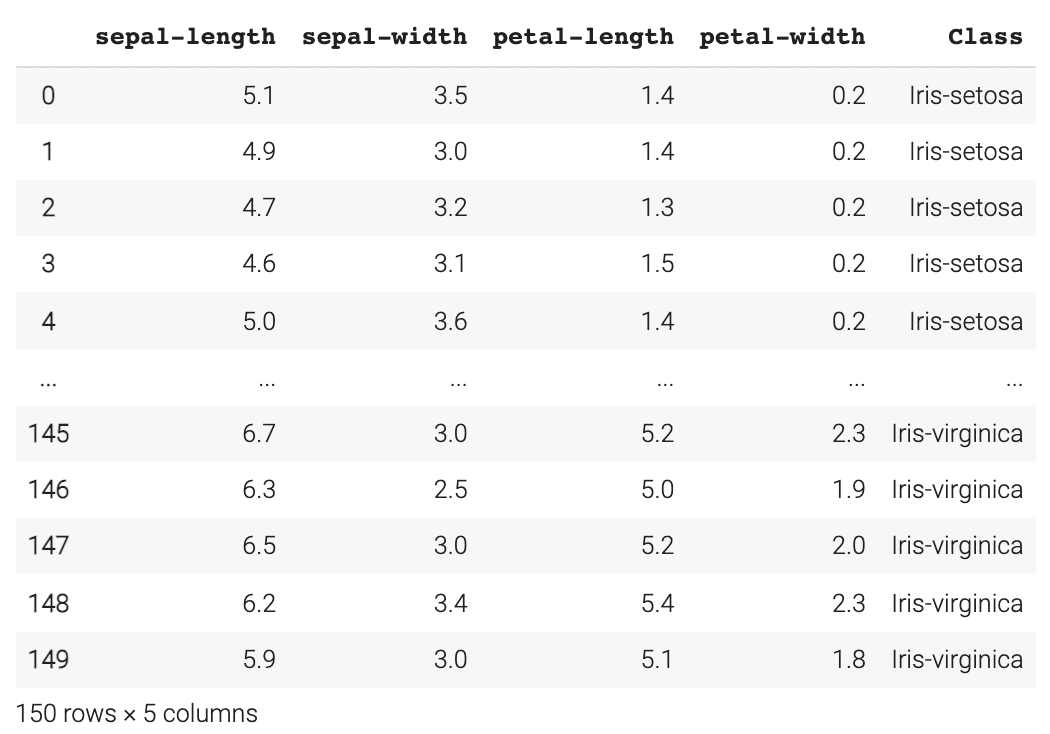
2.加載Iris數據集
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
#指定列名稱
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
#讀入數據集
dataset = pd.read_csv(url, names=names)
至此的執行結果如下所示:
3.數據預處理
這樣做是為了將數據集拆分為屬性和標簽。X變量將包含數據集的前四列,我們稱之為屬性,y變量將包含最后一列,我們稱之為標簽。
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values
4.劃分為訓練集與測試集
在這一步中,我們將把數據集分成訓練和測試兩部分,從而了解算法對訓練數據的學習程度,以及它在測試數據上的表現。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
5.特征縮放
特征縮放是在預測之前對數據預處理的一個重要步驟。下面的方法用于規范化數據的特征范圍。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
6.用KNN做出預測
首先,我們需要從sklearn.neighbors庫導入KNeighborsClassifier類,然后選擇K值。在這個例子中我選擇了7(記住,強烈建議選擇一個奇數值以避免平局情況)。
from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifier(n_neighbors=7)
classifier.fit(X_train, y_train)
然后,我們繼續對測試數據集進行預測。
y_pred = classifier.predict(X_test)
7.算法準確性評估
借助sklearn.metrics庫,我們可以通過分類報告來評估算法的準確性,查看精確度、召回率和F1分數。
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))
下面給出該代碼的執行結果:
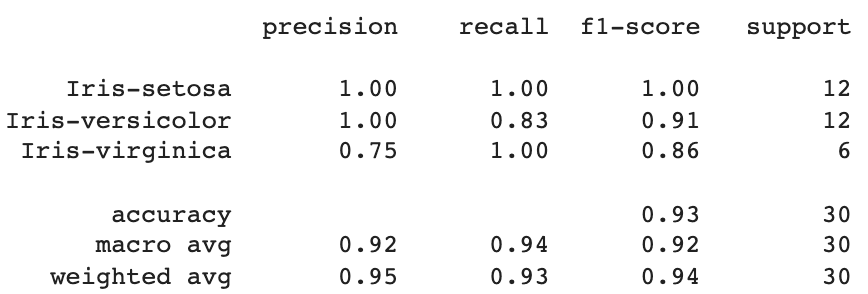
由此我們可以看出,KNN算法對30個數據點進行了分類,平均總準確率為95%,召回率為93%,F1分數為94%。
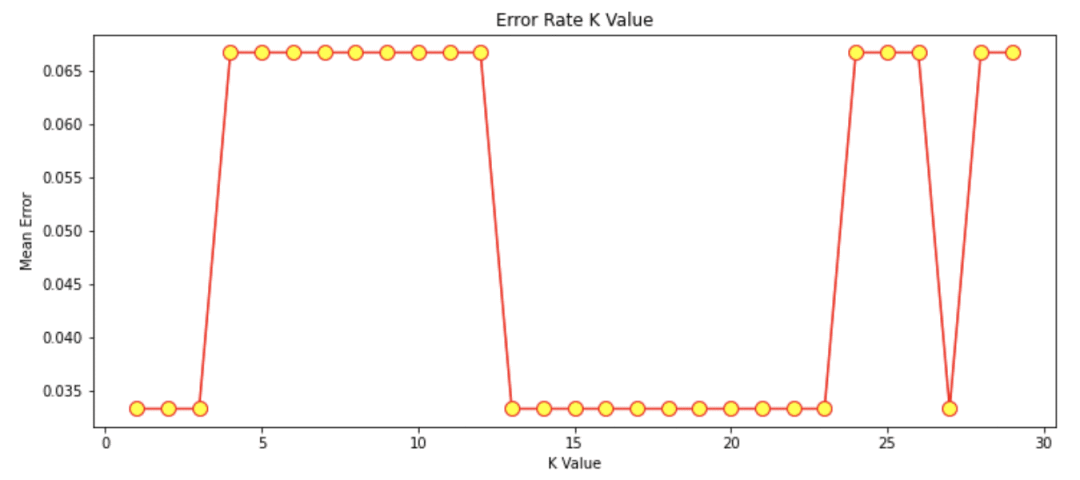
8.找到正確的K值
在本例中,我選擇了K值為7。如果我們想檢查最佳K值是什么,我們可以生成一個圖表以顯示不同的K值及其產生的錯誤率。我將研究1到30之間的K值情況。為此,我們需要在1到30之間執行一個循環,在每次循環期間計算平均誤差并將其添加到誤差列表中。相關代碼如下:
error = []
#計算1到30之間的K值的錯誤率
for i in range(1, 30):
knn = KNeighborsClassifier(n_neighbors=i)
knn.fit(X_train, y_train)
pred_i = knn.predict(X_test)
error.append(np.mean(pred_i != y_test))
繪制K值錯誤率圖:
plt.figure(figsize=(12, 5))
plt.plot(range(1, 30), error, color='red', marker='o',
markerfacecolor='yellow', markersize=10)
plt.title('Error Rate K Value')
plt.xlabel('K Value')
plt.ylabel('Mean Error')
輸出圖形如下:
圖形來源:本文作者例程輸出結果
從上圖可以看出,平均誤差為0的K值主要在k值13-23之間。
五、總結
KNN是一種易于實現的簡單的機器學習算法,可用于執行機器學習過程中的回歸和分類任務。其中,K值是一個參數,表示最近鄰的數值。實際應用中,建議把K值指定為奇數。另外,在KNN算法中你可以選擇不同的距離度量算法(最常見的是使用歐幾里得距離、曼哈頓距離和明可夫斯基距離)。
原文鏈接:https://www.kdnuggets.com/2022/04/nearest-neighbors-classification.html
譯者介紹
朱先忠,51CTO社區編輯,51CTO專家博客、講師,濰坊一所高校計算機教師,自由編程界老兵一枚。早期專注各種微軟技術(編著成ASP.NET AJX、Cocos 2d-X相關三本技術圖書),近十多年投身于開源世界(熟悉流行全棧Web開發技術),了解基于OneNet/AliOS+Arduino/ESP32/樹莓派等物聯網開發技術與Scala+Hadoop+Spark+Flink等大數據開發技術。