[[409098]]

本文轉載自微信公眾號「碼上Java」，作者碼上Java。轉載本文請聯(lián)系碼上Java公眾號。  

前言

面試中經(jīng)常被問到索引相關的問題，其實索引這個概念非常好理解，我們在上學的時候都肯定用過字典吧。索引就像字典的那個目錄，我們可以借助目錄快速檢索到我們所需要的字的解釋。同樣的道理，在數(shù)據(jù)庫中，索引也可以幫助我們快速檢索到我們所需要的數(shù)據(jù)，而且查詢的效率非常高。

總的來說，索引就是一種數(shù)據(jù)結構，我們今天一起來探究一下索引到底什么什么樣的?為什么我們常用B+樹最為索引的數(shù)據(jù)結構呢?

為什么有了索引查詢就會變快?

我們都知道數(shù)據(jù)庫存儲有兩種存儲介質，一個是內(nèi)存，另一個是硬盤。內(nèi)存是一種臨時性存儲介質，而且容量也非常有限，如果服務器斷電的話，會導致數(shù)據(jù)丟失。硬盤是一種永久性存儲介質(如果不損壞的話)，所以說我們需要把數(shù)據(jù)存放在硬盤里面才安全。

但是有個問題?如果我們把數(shù)據(jù)放在硬盤里面的話，我們對其中數(shù)據(jù)進行查詢的時候，就會產(chǎn)生硬盤的I/O操作。相比于內(nèi)存存取來說的話，硬盤在存取時I/O消耗的時間要高很多。而索引的作用就是盡量減少硬盤的I/O操作，從而降低花費的時間。你可以對比查字典的操作，目錄(索引)可以幫你減少翻頁的動作，一個道理。

先聊聊二叉樹

二叉樹，顧名思義，每個節(jié)點最多有兩個“叉”，也就是兩個子節(jié)點，分別是左子節(jié)點和右子節(jié)點。不過，二叉樹并不要求每個節(jié)點都有兩個子節(jié)點，有的節(jié)點只有左子節(jié)點，有的節(jié)點只有右子節(jié)點。

我們先來看下一個最基礎的二叉搜索樹(Binary Search Tree)，搜索某個節(jié)點和插入節(jié)點的規(guī)則一樣，我們假設搜索插入的數(shù)值為 key：

• 如果 key 大于根節(jié)點，則在右子樹中進行查找;
• 如果 key 小于根節(jié)點，則在左子樹中進行查找;
• 如果 key 等于根節(jié)點，也就是找到了這個節(jié)點，返回根節(jié)點即可。

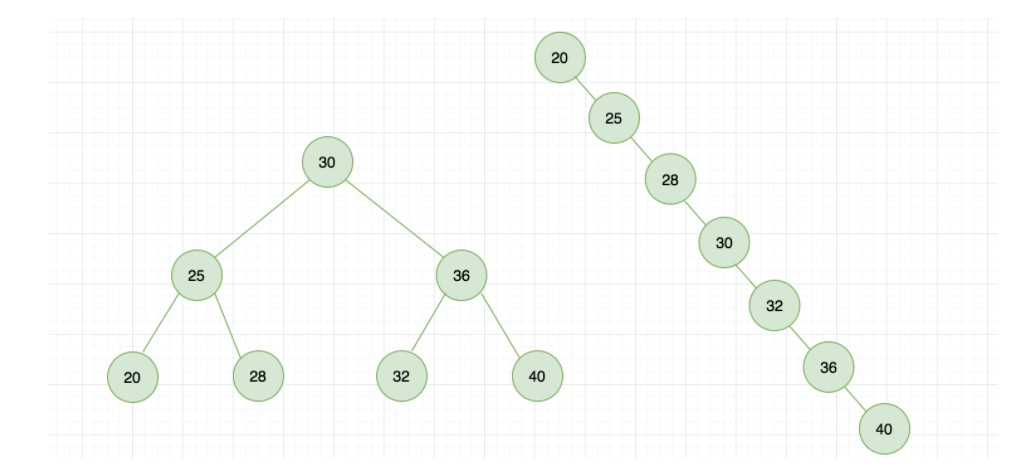
我們舉個例子，創(chuàng)建數(shù)列{30，25，36，32，40，20，28}，同樣的數(shù)據(jù)，不同的插入順序，樹的結果是不一樣的，如下圖所示：

但是存在極端的情況，當二叉樹的深度非常大可能會退化成鏈表。上圖中能看出來第一個樹的深度是 3，也就是說最多只需 3 次比較，就可以找到節(jié)點，而第二個樹的深度是 7，最多需要 7 次比較才能找到節(jié)點。

圖中的右邊也屬于二分查找樹，但是性能方面已經(jīng)退化成了鏈表，查找數(shù)據(jù)的時間復雜度變成了 O(n)。這個問題怎么解決呢?，人們提出了平衡二叉搜索樹(AVL 樹)，它在二分搜索樹的基礎上增加了約束，保證每個節(jié)點的左子樹和右子樹的高度差不能超過 1，也就是說節(jié)點的左子樹和右子樹仍然為平衡二叉樹。

這里說一下，常見的平衡二叉樹有很多種，包括了平衡二叉搜索樹、紅黑樹、數(shù)堆、伸展樹。平衡二叉搜索樹是最早提出來的自平衡二叉搜索樹，當我們提到平衡二叉樹時一般指的就是平衡二叉搜索樹。事實上，第一棵樹就屬于平衡二叉搜索樹，搜索時間復雜度就是 O(log2n)。

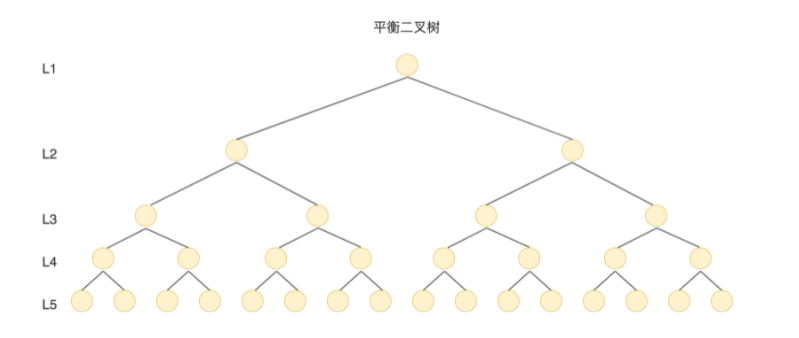
上文中我們提到過查詢時間的多少主要取決于硬盤的I/O操作，如果我們采用二叉樹的形式，即使通過平衡二叉搜索樹進行了改良，樹的深度也是 O(log2n)，當 n 比較大時，深度也是比較高的，比如下圖的情況：

每訪問一次節(jié)點就需要進行一次磁盤 I/O 操作，對于上面的樹來說，我們需要進行 5 次 I/O 操作。雖然平衡二叉樹比較的效率高，但是樹的深度也同樣高，這就意味著磁盤 I/O 操作次數(shù)多，會影響整體數(shù)據(jù)查詢的效率。

再看看什么是 B 樹

在上文中，我們知道了如果二叉樹作為索引會導致樹變的很高，增加硬盤的 I/O 次數(shù)，影響數(shù)據(jù)查詢的時間。B 樹的出現(xiàn)就是為了解決這個問題，B 樹的英文是 Balance Tree，也就是平衡的多路搜索樹，它的高度遠小于平衡二叉樹的高度。在文件系統(tǒng)和數(shù)據(jù)庫系統(tǒng)中的索引結構經(jīng)常采用 B 樹來實現(xiàn)。

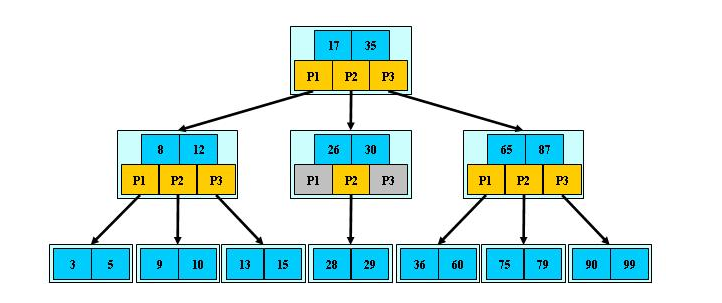
我們來看看B樹結構示意圖，如下圖所示：

B 樹作為平衡的多路搜索樹，它的每一個節(jié)點最多可以包括 M 個子節(jié)點，M 稱為 B 樹的階。在圖中你可以看到，每個磁盤塊中包括了關鍵字和子節(jié)點的指針。如果一個磁盤塊中包括了 x 個關鍵字，那么指針數(shù)就是 x+1。對于一個 100 階的 B 樹來說，如果有 3 層的話最多可以存儲約 100 萬的索引數(shù)據(jù)。對于大量的索引數(shù)據(jù)來說，采用 B 樹的結構是非常適合的，因為樹的高度要遠小于二叉樹的高度。

結合B樹結構示意圖，我們來一起看看B樹是如何進行搜索的，假設我們想要查找的關鍵字是 9，那么步驟可以分為以下幾步：

• 我們與根節(jié)點的關鍵字 (17，35)進行比較，9 小于 17 那么得到指針 P1;
• 按照指針 P1 找到磁盤塊 2，關鍵字為(8，12)，因為 9 在 8 和 12 之間，所以我們得到指針 P2;
• 按照指針 P2 找到磁盤塊 6，關鍵字為(9，10)，然后我們找到了關鍵字 9。

你能看出來在 B 樹的搜索過程中，我們比較的次數(shù)并不少，但如果把數(shù)據(jù)讀取出來然后在內(nèi)存中進行比較，這個時間就是可以忽略不計的。而讀取磁盤塊本身需要進行 I/O 操作，消耗的時間比在內(nèi)存中進行比較所需要的時間要多，是數(shù)據(jù)查找用時的重要因素，B 樹相比于平衡二叉樹來說磁盤 I/O 操作要少，在數(shù)據(jù)查詢中比平衡二叉樹效率要高。

B樹Plus(B+ 樹)

1. B+ 樹是基于B 樹改良過來的，目前主流的數(shù)據(jù)庫都支持B+ 樹作為索引方式，我們以MySQL為例，對比一下B+ 樹和B樹有哪些區(qū)別：
2. B+ 樹中，有 k 個孩子的節(jié)點就有 k 個關鍵字。也就是孩子數(shù)量 = 關鍵字數(shù)，而 B 樹中，孩子數(shù)量 = 關鍵字數(shù) +1。
3. 非葉子節(jié)點的關鍵字也會同時存在在子節(jié)點中，并且是在子節(jié)點中所有關鍵字的最大(或最小)。
4. B+ 樹中，非葉子節(jié)點僅用于索引，不保存數(shù)據(jù)記錄，跟記錄有關的信息都放在葉子節(jié)點中。而 B 樹中，非葉子節(jié)點既保存索引，也保存數(shù)據(jù)記錄。

所有關鍵字都在葉子節(jié)點出現(xiàn)，葉子節(jié)點構成一個有序鏈表，而且葉子節(jié)點本身按照關鍵字的大小從小到大順序鏈接。

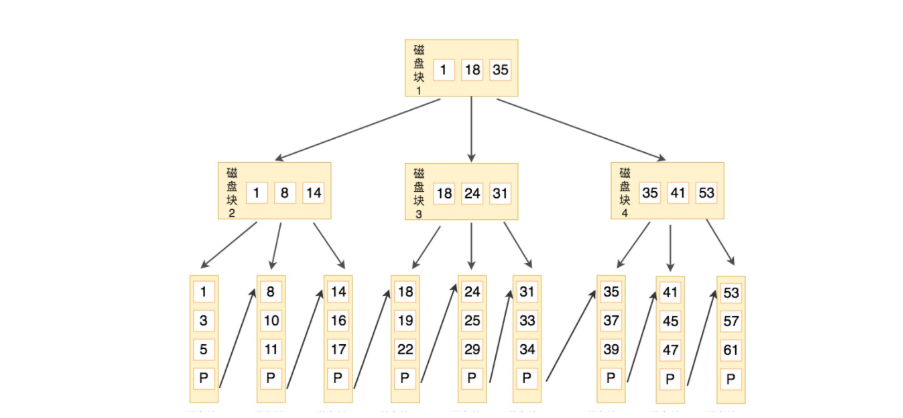
下圖就是一棵 B+ 樹，階數(shù)為 3，根節(jié)點中的關鍵字 1、18、35 分別是子節(jié)點(1，8，14)，(18，24，31)和(35，41，53)中的最小值。每一層父節(jié)點的關鍵字都會出現(xiàn)在下一層的子節(jié)點的關鍵字中，因此在葉子節(jié)點中包括了所有的關鍵字信息，并且每一個葉子節(jié)點都有一個指向下一個節(jié)點的指針，這樣就形成了一個鏈表。

比如，我們想要查找關鍵字 16，B+ 樹會自頂向下逐層進行查找：

1. 與根節(jié)點的關鍵字 (1，18，35) 進行比較，16 在 1 和 18 之間，得到指針 P1(指向磁盤塊 2)
2. 找到磁盤塊 2，關鍵字為(1，8，14)，因為 16 大于 14，所以得到指針 P3(指向磁盤塊 7)
3. 找到磁盤塊 7，關鍵字為(14，16，17)，然后我們找到了關鍵字 16，所以可以找到關鍵字 16 所對應的數(shù)據(jù)。

整個過程一共進行了 3 次 I/O 操作，看起來 B+ 樹和 B 樹的查詢過程差不多，但是 B+ 樹和 B 樹有個根本的差異在于，B+ 樹的中間節(jié)點并不直接存儲數(shù)據(jù)。這樣的好處都有什么呢?

首先，B+ 樹查詢效率更穩(wěn)定。因為 B+ 樹每次只有訪問到葉子節(jié)點才能找到對應的數(shù)據(jù)，而在 B 樹中，非葉子節(jié)點也會存儲數(shù)據(jù)，這樣就會造成查詢效率不穩(wěn)定的情況，有時候訪問到了非葉子節(jié)點就可以找到關鍵字，而有時需要訪問到葉子節(jié)點才能找到關鍵字。

其次，B+ 樹的查詢效率更高，這是因為通常 B+ 樹比 B 樹更矮胖(階數(shù)更大，深度更低)，查詢所需要的磁盤 I/O 也會更少。同樣的磁盤頁大小，B+ 樹可以存儲更多的節(jié)點關鍵字。

不僅是對單個關鍵字的查詢上，在查詢范圍上，B+ 樹的效率也比 B 樹高。這是因為所有關鍵字都出現(xiàn)在 B+ 樹的葉子節(jié)點中，并通過有序鏈表進行了鏈接。而在 B 樹中則需要通過中序遍歷才能完成查詢范圍的查找，效率要低很多。

總結

磁盤的 I/O 操作次數(shù)對索引的使用效率至關重要。雖然傳統(tǒng)的二叉樹數(shù)據(jù)結構查找數(shù)據(jù)的效率高，但很容易增加磁盤 I/O 操作的次數(shù)，影響索引使用的效率。因此在構造索引的時候，我們更傾向于采用“矮胖”的數(shù)據(jù)結構。

B 樹和 B+ 樹都可以作為索引的數(shù)據(jù)結構，在 MySQL 中采用的是 B+ 樹，B+ 樹在查詢性能上更穩(wěn)定，在磁盤頁大小相同的情況下，樹的構造更加矮胖，所需要進行的磁盤 I/O 次數(shù)更少，更適合進行關鍵字的范圍查詢。