成人免费xxxxx在线视频软件_久久精品久久久_亚洲国产精品久久久_天天色天天色_亚洲人成一区_欧美一级欧美三级在线观看

二叉樹的所有路徑：不止遞歸，還有回溯

作者： 程序員Carl
開發 前端
本文我們開始初步涉及到了回溯，很多同學過了這道題目，可能都不知道自己其實使用了回溯，回溯和遞歸都是相伴相生的。

[[415834]]

以為只用了遞歸，其實還用了回溯

二叉樹的所有路徑

題目地址：https://leetcode-cn.com/problems/binary-tree-paths/

給定一個二叉樹，返回所有從根節點到葉子節點的路徑。

說明: 葉子節點是指沒有子節點的節點。

示例:

圖片

思路

這道題目要求從根節點到葉子的路徑，所以需要前序遍歷，這樣才方便讓父節點指向孩子節點，找到對應的路徑。

在這道題目中將第一次涉及到回溯，因為我們要把路徑記錄下來，需要回溯來回退一一個路徑在進入另一個路徑。

前序遍歷以及回溯的過程如圖：

圖片

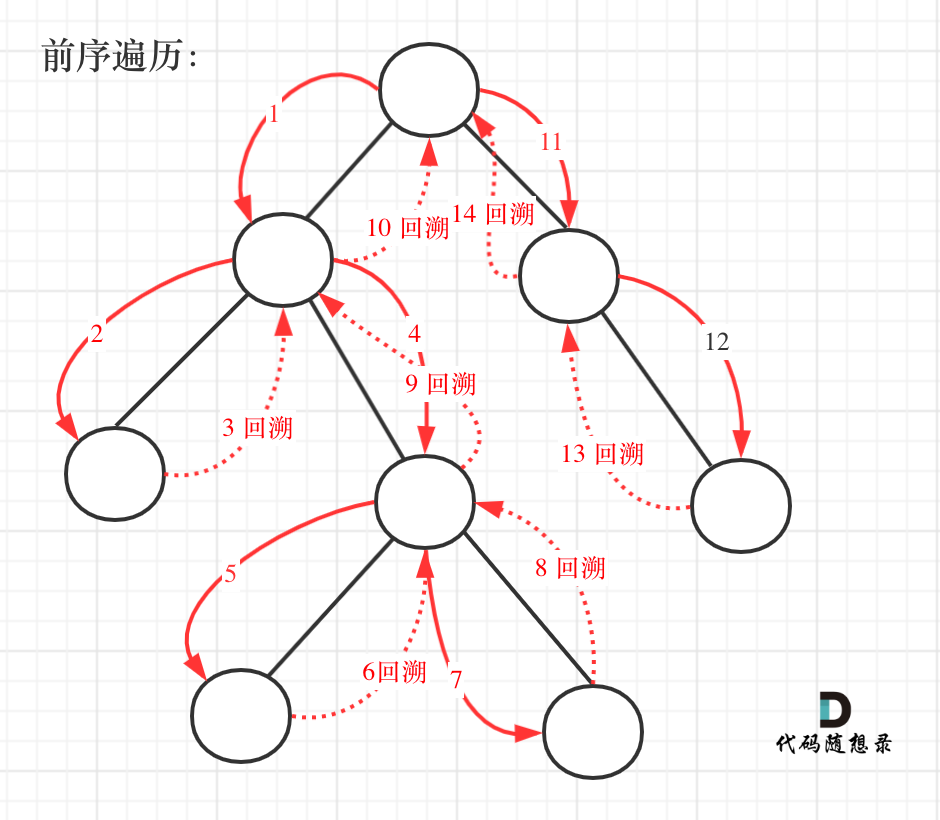
我們先使用遞歸的方式，來做前序遍歷。要知道遞歸和回溯就是一家的，本題也需要回溯。

遞歸

1.遞歸函數函數參數以及返回值

要傳入根節點，記錄每一條路徑的path，和存放結果集的result，這里遞歸不需要返回值，代碼如下：

  1. void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) 

2.確定遞歸終止條件

再寫遞歸的時候都習慣了這么寫：

  1. if (cur == NULL) { 
  2.     終止處理邏輯 
  3. } 

但是本題的終止條件這樣寫會很麻煩，因為本題要找到葉子節點，就開始結束的處理邏輯了(把路徑放進result里)。

那么什么時候算是找到了葉子節點? 是當 cur不為空，其左右孩子都為空的時候，就找到葉子節點。

所以本題的終止條件是：

  1. if (cur->left == NULL && cur->right == NULL) { 
  2.     終止處理邏輯 
  3. } 

為什么沒有判斷cur是否為空呢，因為下面的邏輯可以控制空節點不入循環。

再來看一下終止處理的邏輯。

這里使用vector結構path來記錄路徑，所以要把vector結構的path轉為string格式，在把這個string 放進 result里。

那么為什么使用了vector結構來記錄路徑呢? 因為在下面處理單層遞歸邏輯的時候，要做回溯，使用vector方便來做回溯。

可能有的同學問了，我看有些人的代碼也沒有回溯啊。

其實是有回溯的，只不過隱藏在函數調用時的參數賦值里，下文我還會提到。

這里我們先使用vector結構的path容器來記錄路徑，那么終止處理邏輯如下：

  1. if (cur->left == NULL && cur->right == NULL) { // 遇到葉子節點 
  2.     string sPath; 
  3.     for (int i = 0; i < path.size() - 1; i++) { // 將path里記錄的路徑轉為string格式 
  4.         sPath += to_string(path[i]); 
  5.         sPath += "->"; 
  6.     } 
  7.     sPath += to_string(path[path.size() - 1]); // 記錄最后一個節點（葉子節點） 
  8.     result.push_back(sPath); // 收集一個路徑 
  9.     return; 
  10. } 

3.確定單層遞歸邏輯

因為是前序遍歷，需要先處理中間節點，中間節點就是我們要記錄路徑上的節點，先放進path中。

  1. path.push_back(cur->val); 

然后是遞歸和回溯的過程，上面說過沒有判斷cur是否為空，那么在這里遞歸的時候，如果為空就不進行下一層遞歸了。

所以遞歸前要加上判斷語句，下面要遞歸的節點是否為空，如下

  1. if (cur->left) { 
  2.     traversal(cur->left, path, result); 
  3. } 
  4. if (cur->right) { 
  5.     traversal(cur->right, path, result); 
  6. } 

此時還沒完，遞歸完，要做回溯啊，因為path 不能一直加入節點，它還要刪節點，然后才能加入新的節點。

那么回溯要怎么回溯呢，一些同學會這么寫，如下：

  1. if (cur->left) { 
  2.     traversal(cur->left, path, result); 
  3. } 
  4. if (cur->right) { 
  5.     traversal(cur->right, path, result); 
  6. } 
  7. path.pop_back(); 

這個回溯就要很大的問題，我們知道，回溯和遞歸是一一對應的，有一個遞歸，就要有一個回溯，這么寫的話相當于把遞歸和回溯拆開了， 一個在花括號里，一個在花括號外。

所以回溯要和遞歸永遠在一起，世界上最遙遠的距離是你在花括號里，而我在花括號外!

那么代碼應該這么寫：

  1. if (cur->left) { 
  2.     traversal(cur->left, path, result); 
  3.     path.pop_back(); // 回溯 
  4. } 
  5. if (cur->right) { 
  6.     traversal(cur->right, path, result); 
  7.     path.pop_back(); // 回溯 
  8. } 

那么本題整體代碼如下：

  1. class Solution { 
  2. private: 
  3.  
  4.     void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) { 
  5.         path.push_back(cur->val); 
  6.         // 這才到了葉子節點 
  7.         if (cur->left == NULL && cur->right == NULL) { 
  8.             string sPath; 
  9.             for (int i = 0; i < path.size() - 1; i++) { 
  10.                 sPath += to_string(path[i]); 
  11.                 sPath += "->"; 
  12.             } 
  13.             sPath += to_string(path[path.size() - 1]); 
  14.             result.push_back(sPath); 
  15.             return; 
  16.         } 
  17.         if (cur->left) { 
  18.             traversal(cur->left, path, result); 
  19.             path.pop_back(); // 回溯 
  20.         } 
  21.         if (cur->right) { 
  22.             traversal(cur->right, path, result); 
  23.             path.pop_back(); // 回溯 
  24.         } 
  25.     } 
  26.  
  27. public: 
  28.     vector<string> binaryTreePaths(TreeNode* root) { 
  29.         vector<string> result; 
  30.         vector<int> path; 
  31.         if (root == NULL) return result; 
  32.         traversal(root, path, result); 
  33.         return result; 
  34.     } 
  35. }; 

如上的C++代碼充分體現了回溯。

那么如上代碼可以精簡成如下代碼：

  1. class Solution { 
  2. private: 
  3.  
  4.     void traversal(TreeNode* cur, string path, vector<string>& result) { 
  5.         path += to_string(cur->val); // 中 
  6.         if (cur->left == NULL && cur->right == NULL) { 
  7.             result.push_back(path); 
  8.             return; 
  9.         } 
  10.         if (cur->left) traversal(cur->left, path + "->", result); // 左 
  11.         if (cur->right) traversal(cur->right, path + "->", result); // 右 
  12.     } 
  13.  
  14. public: 
  15.     vector<string> binaryTreePaths(TreeNode* root) { 
  16.         vector<string> result; 
  17.         string path; 
  18.         if (root == NULL) return result; 
  19.         traversal(root, path, result); 
  20.         return result; 
  21.  
  22.     } 
  23. }; 

如上代碼精簡了不少，也隱藏了不少東西。

注意在函數定義的時候void traversal(TreeNode* cur, string path, vector& result) ，定義的是string path，每次都是復制賦值，不用使用引用，否則就無法做到回溯的效果。

那么在如上代碼中，貌似沒有看到回溯的邏輯，其實不然，回溯就隱藏在traversal(cur->left, path + "->", result);中的 path + "->"。 每次函數調用完，path依然是沒有加上"->" 的，這就是回溯了。

為了把這份精簡代碼的回溯過程展現出來，大家可以試一試把：

  1. if (cur->left) traversal(cur->left, path + "->", result); // 左  回溯就隱藏在這里 

改成如下代碼：

  1. path += "->"; 
  2. traversal(cur->left, path, result); // 左 

即：

  1. if (cur->left) { 
  2.     path += "->"; 
  3.     traversal(cur->left, path, result); // 左 
  4. } 
  5. if (cur->right) { 
  6.     path += "->"; 
  7.     traversal(cur->right, path, result); // 右 
  8. } 

此時就沒有回溯了，這個代碼就是通過不了的了。

如果想把回溯加上，就要 在上面代碼的基礎上，加上回溯，就可以AC了。

  1. if (cur->left) { 
  2.     path += "->"; 
  3.     traversal(cur->left, path, result); // 左 
  4.     path.pop_back(); // 回溯 
  5.     path.pop_back(); 
  6. } 
  7. if (cur->right) { 
  8.     path += "->"; 
  9.     traversal(cur->right, path, result); // 右 
  10.     path.pop_back(); // 回溯 
  11.     path.pop_back(); 
  12. } 

大家應該可以感受出來，如果把 path + "->"作為函數參數就是可以的，因為并有沒有改變path的數值，執行完遞歸函數之后，path依然是之前的數值(相當于回溯了)

綜合以上，第二種遞歸的代碼雖然精簡但把很多重要的點隱藏在了代碼細節里，第一種遞歸寫法雖然代碼多一些，但是把每一個邏輯處理都完整的展現了出來了。

迭代法

至于非遞歸的方式，我們可以依然可以使用前序遍歷的迭代方式來模擬遍歷路徑的過程，對該迭代方式不了解的同學，可以看文章二叉樹：聽說遞歸能做的，棧也能做!和二叉樹：前中后序迭代方式統一寫法。

這里除了模擬遞歸需要一個棧，同時還需要一個棧來存放對應的遍歷路徑。

C++代碼如下：

  1. class Solution { 
  2. public: 
  3.     vector<string> binaryTreePaths(TreeNode* root) { 
  4.         stack<TreeNode*> treeSt;// 保存樹的遍歷節點 
  5.         stack<string> pathSt;   // 保存遍歷路徑的節點 
  6.         vector<string> result;  // 保存最終路徑集合 
  7.         if (root == NULL) return result; 
  8.         treeSt.push(root); 
  9.         pathSt.push(to_string(root->val)); 
  10.         while (!treeSt.empty()) { 
  11.             TreeNode* node = treeSt.top(); treeSt.pop(); // 取出節點 中 
  12.             string path = pathSt.top();pathSt.pop();    // 取出該節點對應的路徑 
  13.             if (node->left == NULL && node->right == NULL) { // 遇到葉子節點 
  14.                 result.push_back(path); 
  15.             } 
  16.             if (node->right) { // 右 
  17.                 treeSt.push(node->right); 
  18.                 pathSt.push(path + "->" + to_string(node->right->val)); 
  19.             } 
  20.             if (node->left) { // 左 
  21.                 treeSt.push(node->left); 
  22.                 pathSt.push(path + "->" + to_string(node->left->val)); 
  23.             } 
  24.         } 
  25.         return result; 
  26.     } 
  27. }; 

當然，使用java的同學，可以直接定義一個成員變量為object的棧Stack stack = new Stack<>();，這樣就不用定義兩個棧了，都放到一個棧里就可以了。

總結

本文我們開始初步涉及到了回溯，很多同學過了這道題目，可能都不知道自己其實使用了回溯，回溯和遞歸都是相伴相生的。

我在第一版遞歸代碼中，把遞歸與回溯的細節都充分的展現了出來，大家可以自己感受一下。

第二版遞歸代碼對于初學者其實非常不友好，代碼看上去簡單，但是隱藏細節于無形。

最后我依然給出了迭代法。

對于本地充分了解遞歸與回溯的過程之后，有精力的同學可以在去實現迭代法。

其他語言版本

Java：

  1. //解法一 
  2. class Solution { 
  3.     /** 
  4.      * 遞歸法 
  5.      */ 
  6.     public List<String> binaryTreePaths(TreeNode root) { 
  7.         List<String> res = new ArrayList<>(); 
  8.         if (root == null) { 
  9.             return res; 
  10.         } 
  11.         List<Integer> paths = new ArrayList<>(); 
  12.         traversal(root, paths, res); 
  13.         return res; 
  14.     } 
  15.  
  16.     private void traversal(TreeNode root, List<Integer> paths, List<String> res) { 
  17.         paths.add(root.val); 
  18.         // 葉子結點 
  19.         if (root.left == null && root.right == null) { 
  20.             // 輸出 
  21.             StringBuilder sb = new StringBuilder(); 
  22.             for (int i = 0; i < paths.size() - 1; i++) { 
  23.                 sb.append(paths.get(i)).append("->"); 
  24.             } 
  25.             sb.append(paths.get(paths.size() - 1)); 
  26.             res.add(sb.toString()); 
  27.             return; 
  28.         } 
  29.         if (root.left != null) { 
  30.             traversal(root.left, paths, res); 
  31.             paths.remove(paths.size() - 1);// 回溯 
  32.         } 
  33.         if (root.right != null) { 
  34.             traversal(root.right, paths, res); 
  35.             paths.remove(paths.size() - 1);// 回溯 
  36.         } 
  37.     } 
  38. } 

Python：

  1. class Solution: 
  2.     def binaryTreePaths(self, root: TreeNode) -> List[str]: 
  3.         path=[] 
  4.         res=[] 
  5.         def backtrace(root, path): 
  6.             if not root:return  
  7.             path.append(root.val) 
  8.             if (not root.left)and (not root.right): 
  9.                res.append(path[:]) 
  10.             ways=[] 
  11.             if root.left:ways.append(root.left) 
  12.             if root.right:ways.append(root.right) 
  13.             for way in ways: 
  14.                 backtrace(way,path) 
  15.                 path.pop() 
  16.         backtrace(root,path) 
  17.         return ["->".join(list(map(str,i))) for i in res] 

Go：

  1. func binaryTreePaths(root *TreeNode) []string { 
  2.     res := make([]string, 0) 
  3.     var travel func(node *TreeNode, s string) 
  4.     travel = func(node *TreeNode, s string) { 
  5.         if node.Left == nil && node.Right == nil { 
  6.             v := s + strconv.Itoa(node.Val) 
  7.             res = append(res, v) 
  8.             return 
  9.         } 
  10.         s = s + strconv.Itoa(node.Val) + "->" 
  11.         if node.Left != nil { 
  12.             travel(node.Left, s) 
  13.         } 
  14.         if node.Right != nil { 
  15.             travel(node.Right, s) 
  16.         } 
  17.     } 
  18.     travel(root, "") 
  19.     return res 
  20. } 

 

責任編輯：姜華 來源： 代碼隨想錄
二叉樹遞歸回溯
相關推薦

2020-04-27 07:05:58

二叉樹左子樹右子樹

2021-09-15 07:40:50

二叉樹數據結構算法

2021-04-19 07:47:42

數據結構二叉樹Tree

2021-04-20 08:37:14

數據結構二叉樹樹

2021-07-13 11:32:41

二叉樹數據結構算法

2022-11-06 19:43:10

二叉樹指針節點

2021-12-05 18:25:12

二叉樹路徑節點

2022-10-26 23:58:02

二叉樹數組算法

2013-07-15 16:35:55

二叉樹迭代器

2021-03-17 08:19:22

二叉樹LeetCode樹

2021-04-28 20:12:27

數據結構創建

2021-08-27 11:36:44

二叉樹回溯節點

2021-09-29 10:19:00

算法平衡二叉樹

2020-09-23 18:25:40

算法二叉樹多叉樹

2018-03-15 08:31:57

二叉樹存儲結構

2021-05-06 17:46:30

二叉樹數據結構

2021-09-15 07:56:32

二叉樹層次遍歷

2021-10-12 09:25:11

二叉樹樹形結構

2021-03-22 08:23:29

LeetCode二叉樹節點

2023-05-08 15:57:16

二叉樹數據結構
點贊
收藏

51CTO技術棧公眾號

主站蜘蛛池模板： 国产成人网 | 色狠狠一区 | 欧美激情黄色 | 久久麻豆精品 | av一二三区| 毛片在线看片 | 国产精品一区久久久 | 国产小视频在线观看 | 亚洲免费在线观看 | 夜夜av| 一区二区三区四区在线视频 | 国产精品成人一区 | 中文字幕视频在线观看 | 91久久精品国产91久久 | 一区二区三区四区不卡视频 | 国产精品.xx视频.xxtv | 亚洲美女av网站 | 99日韩 | 天天玩夜夜操 | 国产精品毛片无码 | 免费一级欧美在线观看视频 | 欧美电影免费网站 | 天天综合网天天综合色 | 欧美人成在线视频 | 午夜视频免费在线 | av免费网址 | 黄色国产大片 | 久色| 国产91久久精品一区二区 | 国产亚洲一级 | 国产一区二区三区久久久久久久久 | 四虎影视1304t | 国产成人精品久久二区二区91 | 91精品国产综合久久婷婷香蕉 | 国产成年人小视频 | 欧美日在线 | 国产在线97 | 久久综合九色综合欧美狠狠 | 亚洲成人三区 | 中文字幕精品一区久久久久 | 久久五月婷 |