[[397667]]

這假期咋就唰的一下就沒啦，昨天還跟放假第一天似的，今天就開始上班了。

既然開工了，那咱們就隨遇而安唄，繼續(xù)努力搬磚吧。

下面我們將鏡頭切到袁記菜館。

小二：掌柜的，最近大家都在忙著種樹，說是要保護環(huán)境。

老板娘：樹 ? 咱們店有呀，前幾年種的那棵葡萄樹，不是都結(jié)果子了嗎?就數(shù)你吃的最多。

小兒：這.......。

大家應(yīng)該猜到，咱們今天要嘮啥了。

之前給大家介紹了鏈表,棧，哈希表 等數(shù)據(jù)結(jié)構(gòu)

今天咱們來看一種新的數(shù)據(jù)結(jié)構(gòu)，樹。

PS：本篇文章內(nèi)容較基礎(chǔ)，對于沒有學(xué)過數(shù)據(jù)結(jié)構(gòu)的同學(xué)會有一些幫助，如果你已經(jīng)學(xué)過的話，也可以復(fù)習(xí)一下，查缺補漏，后面會繼續(xù)更新這個系列。

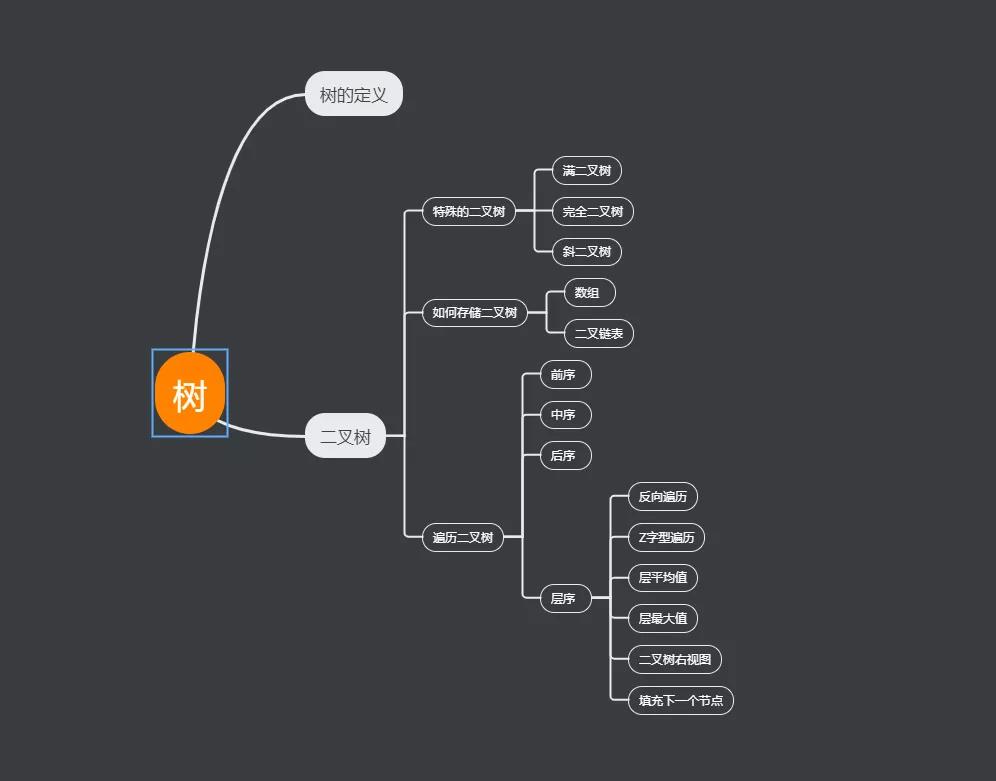
本文大綱

本文大綱

注：可能有的同學(xué)不喜歡手機閱讀，所以將這篇同步在了我的倉庫，大家可以去 Github 進行閱讀，點擊文章最下方的閱讀原文即可

樹

我們先來看下百度百科對樹的定義

樹是 n (n >= 0) 個節(jié)點的有限集。n = 0 時 我們稱之為空樹, 空樹是樹的特例。

在任意一棵非空樹中：

• 有且僅有一個特定的節(jié)點稱為根(Root)的節(jié)點
• 當(dāng) n > 1 時，其余節(jié)點可分為 m (m > 0)個互不相交的有限集 T1、T2、........Tm，其中每一個集合本身又是一棵樹，并且稱為根的子樹。

我們一起來拆解一下上面的兩句話，到底什么是子樹呢?見下圖

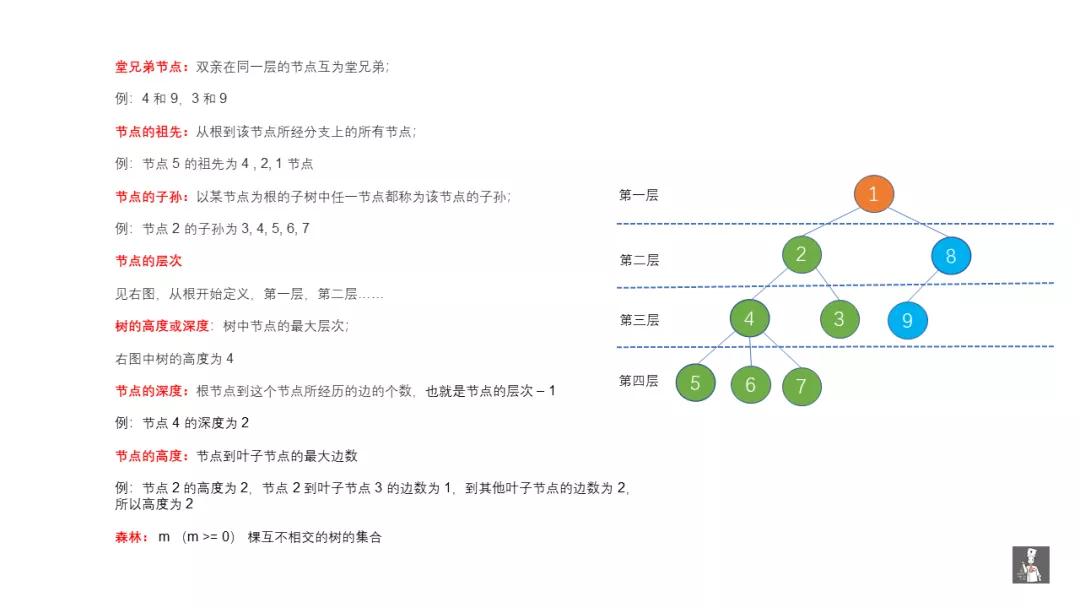
樹

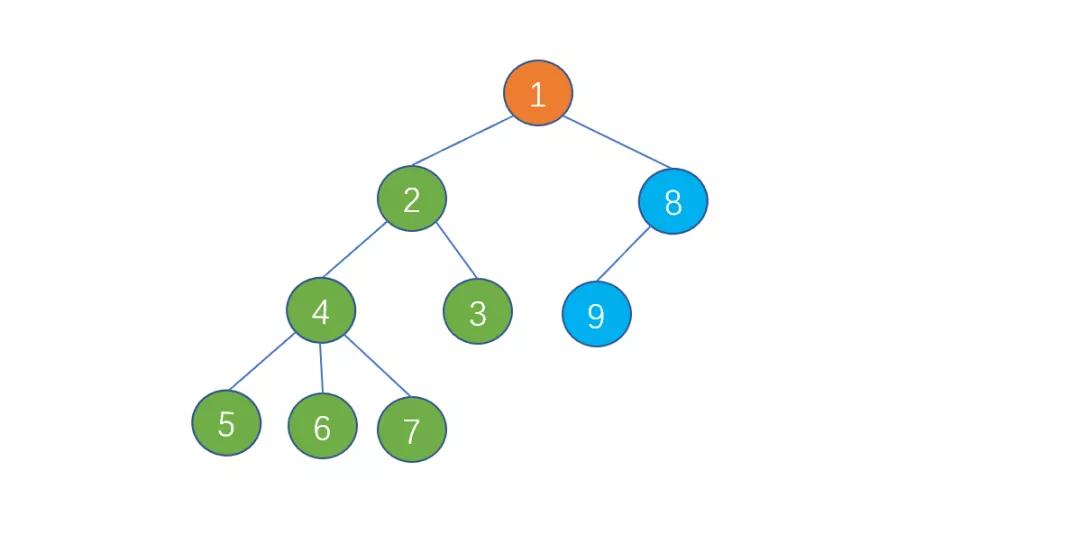
例如在上面的圖中

有且僅有一個特定的節(jié)點稱為根節(jié)點，也就是上圖中的橙色節(jié)點。

當(dāng)節(jié)點數(shù)目大于 1 時，除根節(jié)點以外的節(jié)點，可分為 m 個互不相交的有限集 T1,T2........Tm。

例如上圖中，我們將根節(jié)點以外的節(jié)點，分為了 T1 (2，3，4，5，6，7)，T2(8，9)兩個有限集。

那么 T1 (綠色節(jié)點)和 T2(藍(lán)色節(jié)點)就是根節(jié)點(橙色節(jié)點)的子樹。

我們拆解之后發(fā)現(xiàn)，我們上圖中的例子符合樹的要求，另外不知道大家有沒有注意到這個地方。

除根節(jié)點以外的節(jié)點，可分為 m 個互不相交的有限集。

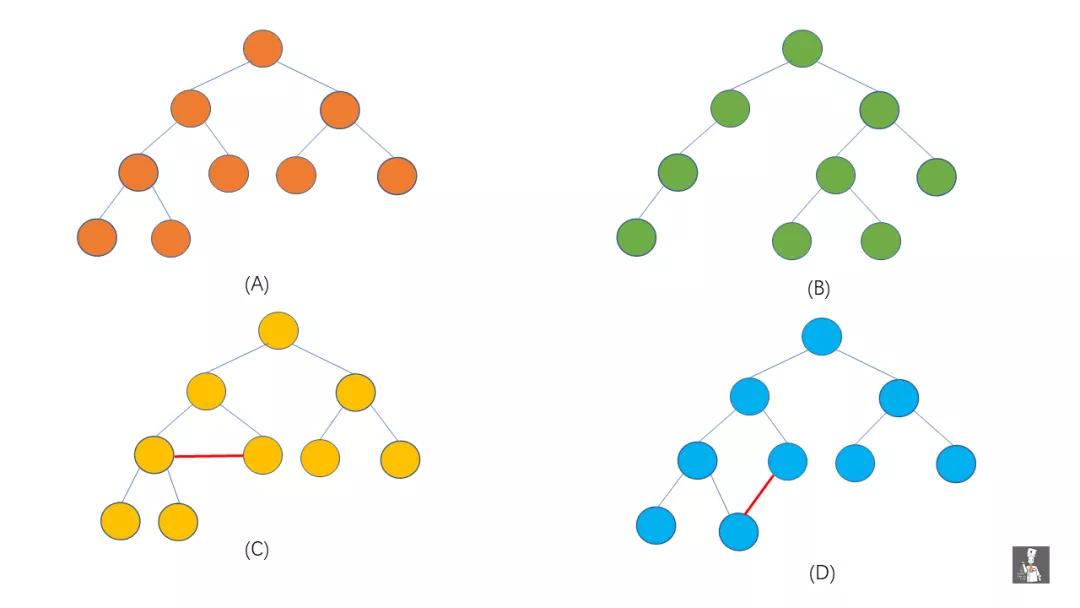
那么這個互不相交又是什么含義呢?見下圖。

我們將 (A) , (B) , (C) , (D) 代入上方定義中發(fā)現(xiàn)，(A) , (B) 符合樹的定義，(C), (D) 不符合，這是因為 (C) , (D) 它們都有相交的子樹。

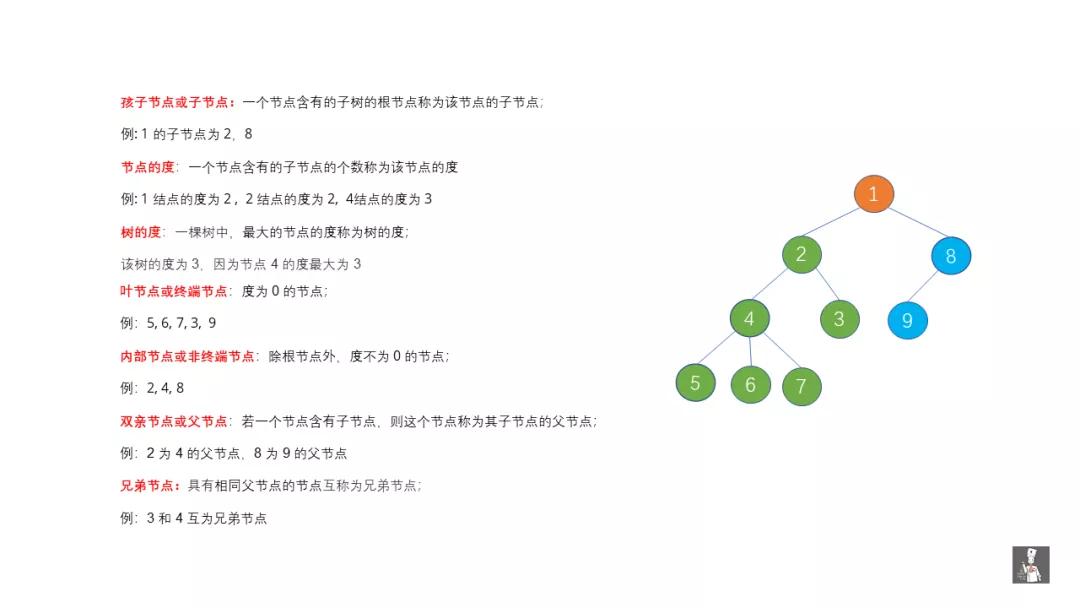
好啦，到這里我們知道如何辨別樹啦，下面我們通過下面兩張圖再來深入了解一下樹。

主要從節(jié)點類型，節(jié)點間的關(guān)系下手。

這里節(jié)點的高度和深度

可能容易記混，我們代入到現(xiàn)實即可。

我們求物體深度時，從上往下測量，求高度時，從下往上測量，節(jié)點的高度和深度也是如此。

二叉樹

我們刷題時遇到的就是二叉樹啦，下面我們一起來了解一下二叉樹

二叉樹前提是一棵樹，也就是需要滿足我們樹的定義的同時，還需要滿足以下要求

每個節(jié)點最多有兩個子節(jié)點，分別是左子節(jié)點和右子節(jié)點。

注意我們這里提到的是最多，所以二叉樹并不是必須要求每個節(jié)點都有兩個子節(jié)點，也可以有的僅有一個左子節(jié)點，有的節(jié)點僅有一個右子節(jié)點。

下面我們來總結(jié)一下二叉樹的特點

• 每個節(jié)點最多有兩棵子樹，也就是說二叉樹中不存在度大于 2 的節(jié)點，節(jié)點的度可以為 0，1，2。
• 左子樹和右子樹是有順序的,有左右之分。
• 假如只有一棵子樹 ，也要區(qū)分它是左子樹還是右子樹

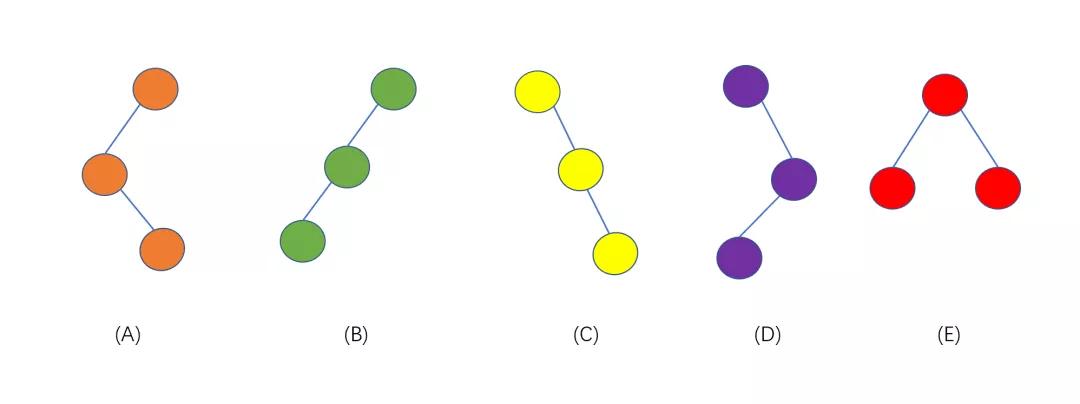
好啦，我們已經(jīng)了解了二叉樹的特點，那我們分析一下，下圖中的樹是否滿足二叉樹定義，共有幾種二叉樹。

上圖共為 5 種不同的二叉樹，在二叉樹的定義中提到，二叉樹的左子樹和右子樹是有順序的，所以 B，C 是兩個不同的二叉樹，故上圖為 5 種不同的二叉樹。

特殊的二叉樹

下面我們來說幾種比較特殊的二叉樹，可以幫助我們刷題時，考慮到特殊情況。

滿二叉樹

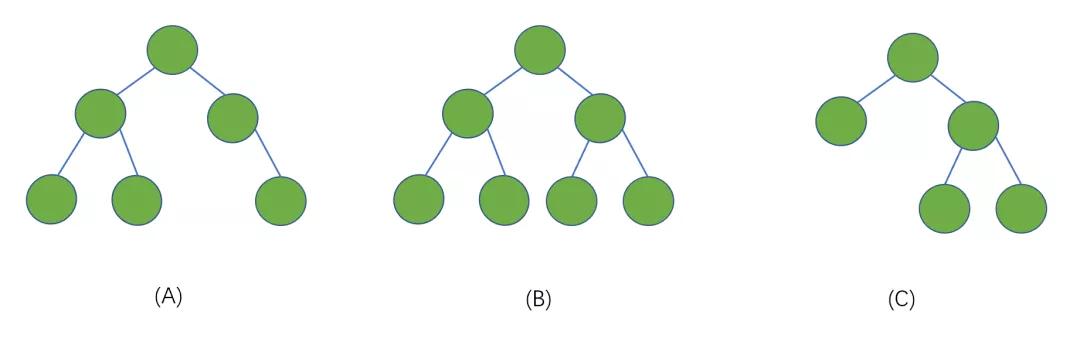
滿二叉樹：在一棵二叉樹中，所有分支節(jié)點都存在左子樹和右子樹，并且所有的葉子都在同一層,這種樹我們稱之為滿二叉樹.見下圖

我們發(fā)現(xiàn)只有 (B) 符合滿二叉樹的定義,我們發(fā)現(xiàn)其實滿二叉樹也為完全二叉樹的一種。

完全二叉樹

完全二叉樹：葉子結(jié)點只能出現(xiàn)在最下層和次下層，且最下層的葉子結(jié)點集中在樹的左部。

哦!我們可以這樣理解，除了最后一層，其他層的節(jié)點個數(shù)都是滿的，而且最后一層的葉子節(jié)點必須靠左。

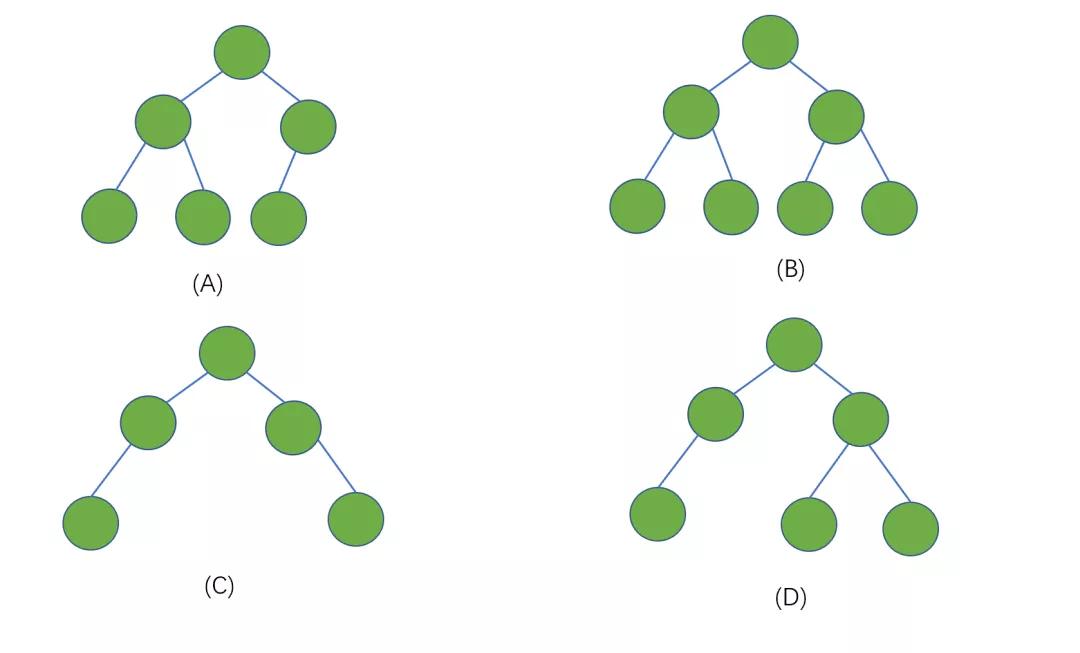
下面我們來看一下這幾個例子

上面的幾個例子中，(A)(B)為完全二叉樹，(C)(D)不是完全二叉樹

斜二叉樹

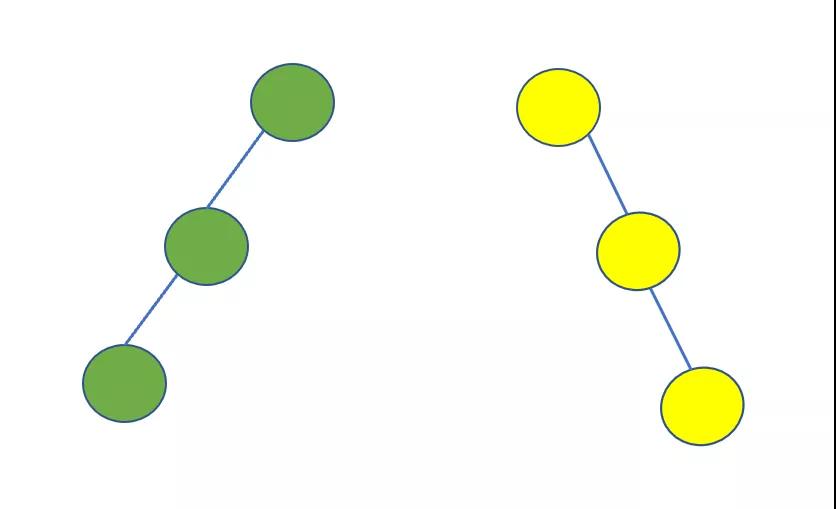
這個就很好理解啦,斜二叉樹也就是斜的二叉樹,所有的節(jié)點只有左子樹的稱為左斜樹,所有節(jié)點只有右子樹的二叉樹稱為右斜樹.

諾,下面這倆就是.

另外還有 一些二叉樹的性質(zhì), 比如第 i 層至多有多少節(jié)點,通過葉子節(jié)點求度為 2 的節(jié)點, 通過節(jié)點樹求二叉樹的深度等, 這些是考研常考的知識, 就不在這里進行贅述,需要的同學(xué)可以看一下王道或者天勤的數(shù)據(jù)結(jié)構(gòu), 上面描述的很具體, 并附有證明過程.

好啦，我們已經(jīng)了解了二叉樹，那么二叉樹如何存儲呢?

如何存儲二叉樹

二叉樹多采用兩種方法進行存儲,基于數(shù)組的順序存儲法和基于指針的二叉鏈?zhǔn)酱鎯Ψ?/p>

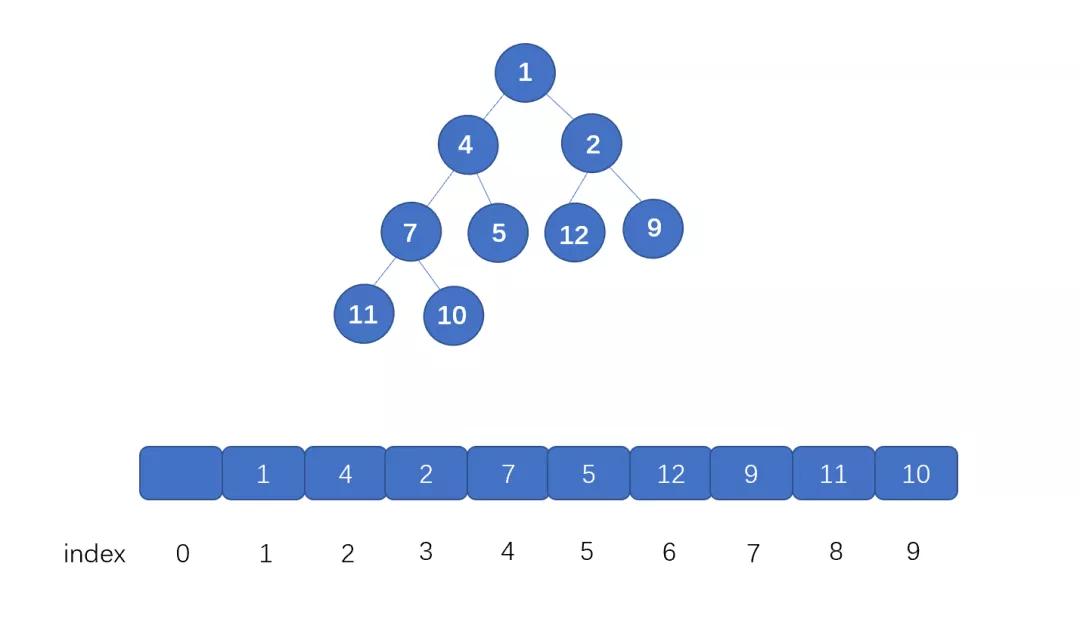
這里我們再來回顧一下如何用數(shù)組存儲完全二叉樹.

我們首先看根節(jié)點，也就是值為 1 的節(jié)點，它在數(shù)組中的下標(biāo)為 1 ,它的左子節(jié)點，也就是值為 4 的節(jié)點，此時索引為 2，右子節(jié)點也就是值為 2 的節(jié)點，它的索引為 3。

我們發(fā)現(xiàn)其中的關(guān)系了嗎?

數(shù)組中，某節(jié)點(非葉子節(jié)點)的下標(biāo)為 i , 那么其左子節(jié)點下標(biāo)為 2*i(這里可以直接通過相乘得到左孩子, 也就是為什么空出第一個位置, 如果從 0 開始存，則需要 2i+1 才行), 右子節(jié)點為 2i+1，其父節(jié)點為 i/2 。既然我們完全可以根據(jù)索引找到某節(jié)點的 左子節(jié)點 和右子節(jié)點，那么我們用數(shù)組存儲是完全沒有問題的。

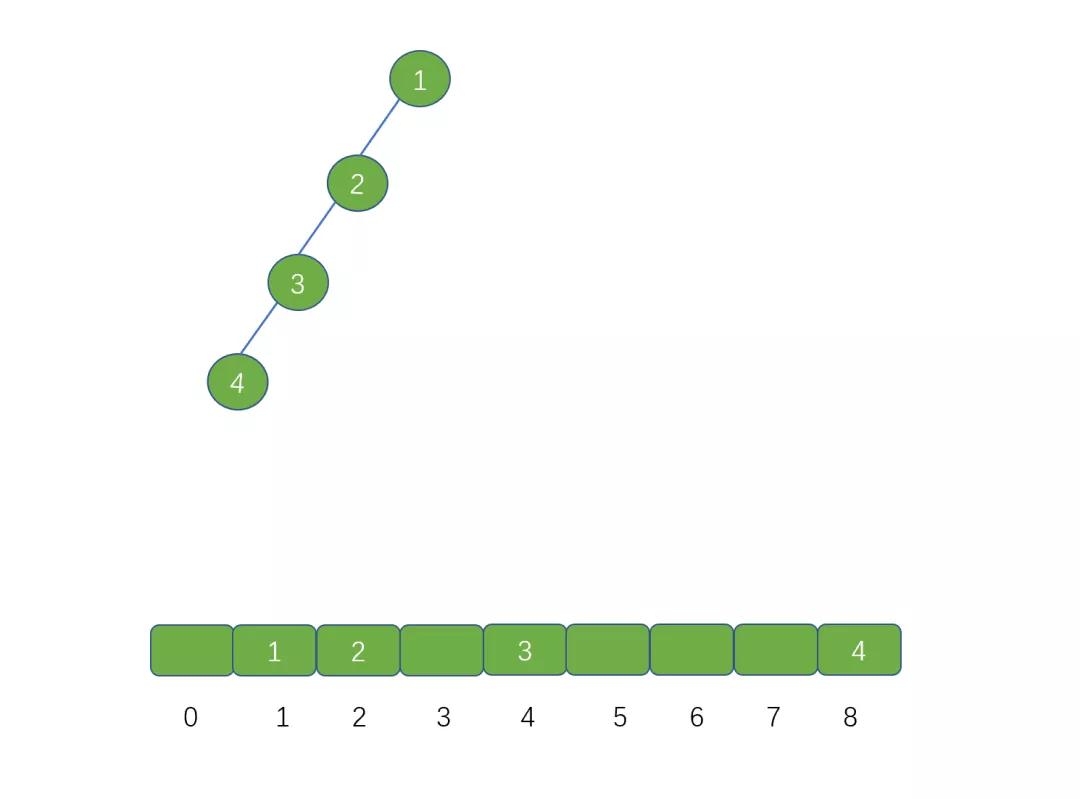
但是,我們再考慮一下這種情景,如果我們用數(shù)組存儲斜樹時會出現(xiàn)什么情況?

通過 2*i 進行存儲左子節(jié)點的話,如果遇到斜樹時,則會浪費很多的存儲空間,這樣顯然是不合適的,

所以說當(dāng)存儲完全二叉樹時,我們用數(shù)組存儲,無疑是最省內(nèi)存的，但是存儲斜樹時，則就不太合適。

所以我們下面介紹一下另一種存儲結(jié)構(gòu),鏈?zhǔn)酱鎯Y(jié)構(gòu).

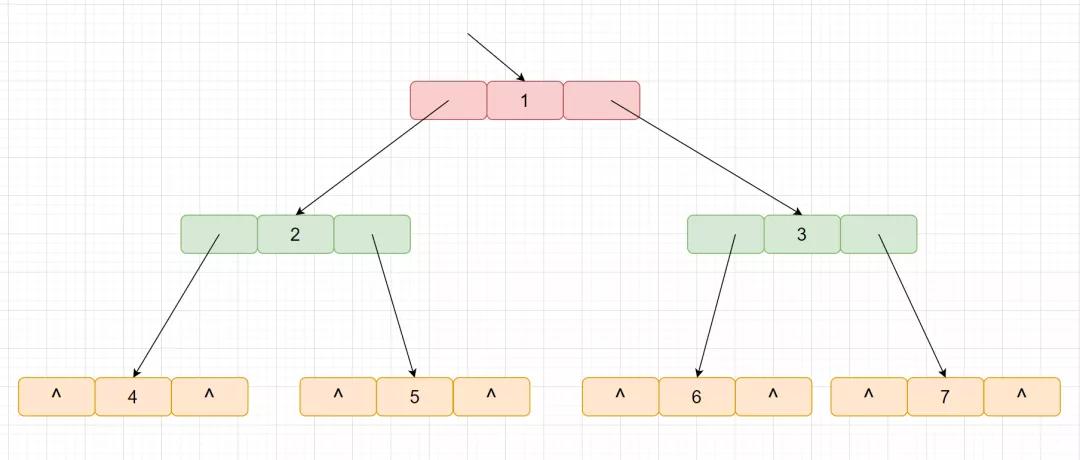
因為二叉樹的每個節(jié)點, 最多有兩個孩子, 所以我們只需為每個節(jié)點定義一個數(shù)據(jù)域,兩個指針域即可

val 為節(jié)點的值, left 指向左子節(jié)點, right 指向右子節(jié)點。

下面我們對樹 1, 2, 3, 4, 5, 6, 7 使用鏈?zhǔn)酱鎯Y(jié)構(gòu)進行存儲,即為下面這種情況。

二叉鏈表的節(jié)點結(jié)構(gòu)定義代碼

public class BinaryTree { 
    int val; 
    BinaryTree left; 
    BinaryTree right; 
    BinaryTree() {} 
    BinaryTree(int val) { this.val = val; } 
    BinaryTree(int val, BinaryTree left, BinaryTree right) { 
        this.val = val; 
        this.left = left; 
        this.right = right; 
    } 
} 

另外我們在刷題的時候, 可以自己實現(xiàn)一下數(shù)據(jù)結(jié)構(gòu), 加深我們的理解, 提升基本功, 而且面試考的也越來越多.

好啦,下面我們說一下樹的遍歷,

下面我會用動圖的形式進行描述,很容易理解, 我也會為大家總結(jié)對應(yīng)的題目,歡迎各位閱讀.

遍歷二叉樹

二叉樹的遍歷指從根節(jié)點出發(fā),按照某種次序依次訪問二叉樹的所有節(jié)點,使得每個節(jié)點都被訪問且訪問一次.

我們下面介紹二叉樹的幾種遍歷方法及其對應(yīng)的題目, 前序遍歷, 中序遍歷 , 后序遍歷 , 層序遍歷 .

前序遍歷

前序遍歷的順序是, 對于樹中的某節(jié)點,先遍歷該節(jié)點,然后再遍歷其左子樹,最后遍歷其右子樹.

只看文字有點生硬, 下面我們直接看動畫吧

前序遍歷

測試題目: leetcode 144. 二叉樹的前序遍歷

代碼實現(xiàn)(遞歸版)

class Solution { 
    public List<Integer> preorderTraversal(TreeNode root) { 
        List<Integer> arr = new ArrayList<>(); 
        preorder(root,arr); 
        return arr; 
 
    } 
    public void preorder(TreeNode root,List<Integer> arr) { 
        if (root == null) { 
            return; 
        } 
        arr.add(root.val); 
        preorder(root.left,arr); 
        preorder(root.right,arr); 
    } 
} 

時間復(fù)雜度 : O(n) 空間復(fù)雜度 : O(n) 為遞歸過程中棧的開銷,平均為 O(logn),但是當(dāng)二叉樹為斜樹時則為 O(n)

為了控制文章篇幅, 二叉樹的迭代遍歷形式, 會在下篇文章進行介紹。

中序遍歷

中序遍歷的順序是, 對于樹中的某節(jié)點,先遍歷該節(jié)點的左子樹, 然后再遍歷該節(jié)點, 最后遍歷其右子樹

繼續(xù)看動畫吧, 如果有些遺忘或者剛開始學(xué)數(shù)據(jù)結(jié)構(gòu)的同學(xué)可以自己模擬一下執(zhí)行步驟.

中序遍歷

測試題目: leetcode 94 題 二叉樹的中序遍歷

代碼實現(xiàn)(遞歸版)

class Solution { 
    public List<Integer> inorderTraversal(TreeNode root) { 
          
         List<Integer> res = new ArrayList<>(); 
         inorder(root, res); 
         return res; 
 
    } 
    public void inorder (TreeNode root, List<Integer> res) { 
        if (root == null) { 
            return; 
        } 
        inorder(root.left, res); 
        res.add(root.val); 
        inorder(root.right, res); 
 
    } 
} 

時間復(fù)雜度 : O(n) 空間復(fù)雜度 : O(n)

后序遍歷

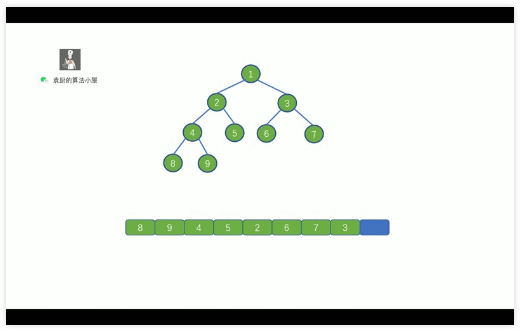
后序遍歷的順序是,對于樹中的某節(jié)點, 先遍歷該節(jié)點的左子樹, 再遍歷其右子樹, 最后遍歷該節(jié)點.

哈哈,繼續(xù)看動畫吧,看完動畫就懂啦.

后序遍歷

測試題目: leetcode 145 題 二叉樹的后序遍歷

代碼實現(xiàn)(遞歸版)

class Solution { 
    public List<Integer> postorderTraversal(TreeNode root) { 
         List<Integer> res = new ArrayList<>(); 
         postorder(root,res); 
         return res; 
    } 
 
    public void postorder(TreeNode root, List<Integer> res) { 
        if (root == null) { 
            return; 
        } 
        postorder(root.left, res); 
        postorder(root.right, res); 
        res.add(root.val); 
    } 
} 

時間復(fù)雜度 : O(n) 空間復(fù)雜度 : O(n)

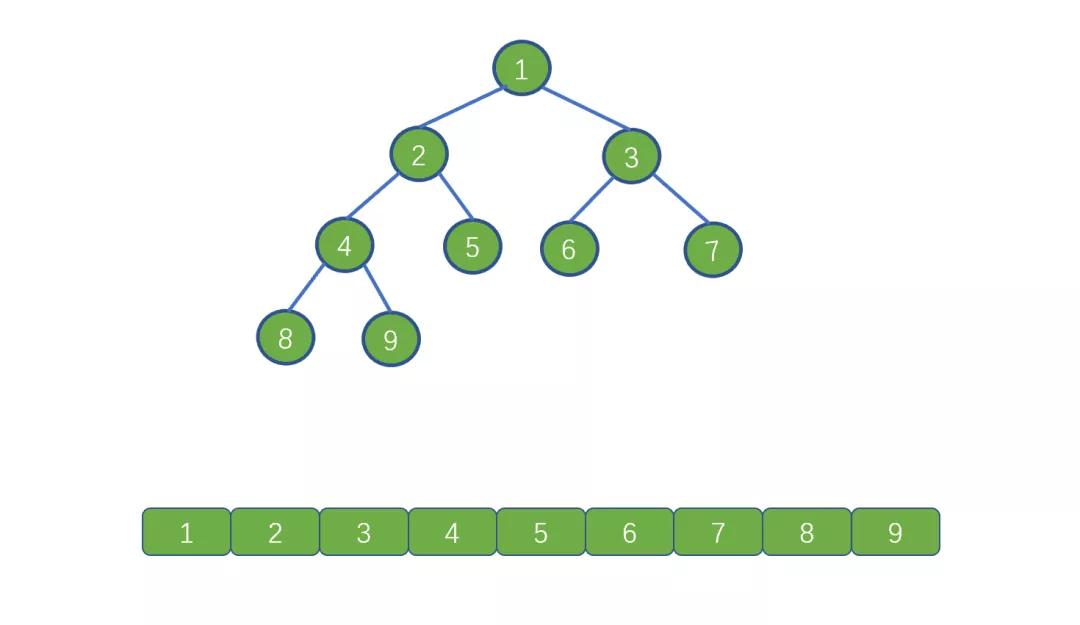
層序遍歷

顧名思義,一層一層的遍歷.

比如剛才那棵二叉樹的層序遍歷序列即為 1 ~ 9.

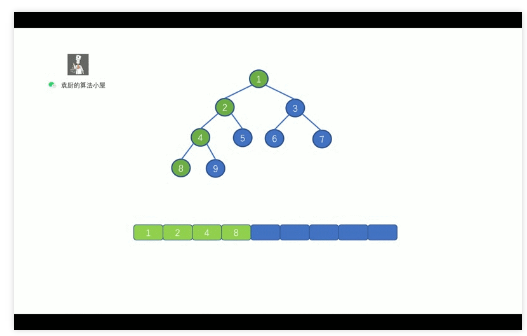
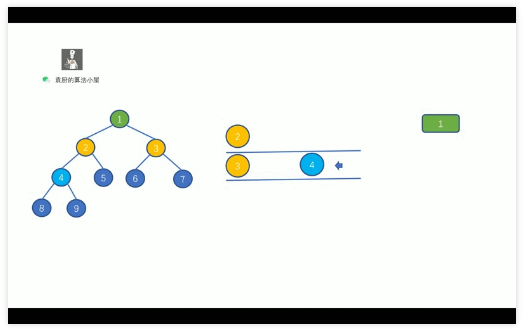
二叉樹的層序, 這里我們需要借助其他數(shù)據(jù)結(jié)構(gòu)來實現(xiàn), 我們思考一下, 我們需要對二叉樹進行層次遍歷, 從上往下進行遍歷, 我們可以借助什么數(shù)據(jù)結(jié)構(gòu)來幫我們呢 ?

我們可以利用隊列先進先出的特性，使用隊列來幫助我們完成層序遍歷, 具體操作如下

讓二叉樹的每一層入隊, 然后再依次執(zhí)行出隊操作,

對該層節(jié)點執(zhí)行出隊操作時, 需要將該節(jié)點的左孩子節(jié)點和右孩子節(jié)點進行入隊操作,

這樣當(dāng)該層的所有節(jié)點出隊結(jié)束后, 下一層也就入隊完畢,

不過我們需要考慮的就是, 我們需要通過一個變量來保存每一層節(jié)點的數(shù)量.

這樣做是為了防止, 一直執(zhí)行出隊操作, 使輸出不能分層

好啦,下面我們直接看動畫吧,

測試題目: leetcode 102 二叉樹的層序遍歷

題目代碼

class Solution { 
    public List<List<Integer>> levelOrder(TreeNode root) { 
     
      List<List<Integer>> res = new ArrayList<>(); 
      if (root == null) { 
          return res; 
      }  
      //入隊 root 節(jié)點，也就是第一層   
      Queue<TreeNode> queue = new LinkedList<>(); 
      queue.offer(root); 
      while (!queue.isEmpty()) { 
          List<Integer> list = new ArrayList<>(); 
          int size = queue.size(); 
          for (int i = 0; i < size; ++i) { 
              TreeNode temp = queue.poll(); 
              //孩子節(jié)點不為空，則入隊 
              if (temp.left != null)  queue.offer(temp.left); 
              if (temp.right != null) queue.offer(temp.right); 
              list.add(temp.val); 
          } 
          res.add(list); 
      } 
      return res; 
    } 
} 

時間復(fù)雜度：O(n) 空間復(fù)雜度：O(n)

大家如果吃透了二叉樹的層序遍歷的話，可以順手把下面幾道題目解決掉，思路一致，甚至都不用拐彎

• leetcode 107. 二叉樹的層序遍歷 II
• leetcode 103. 二叉樹的鋸齒形層序遍歷

上面兩道題僅僅是多了翻轉(zhuǎn)

• leetcode 199. 二叉樹的右視圖
• leetcode 515. 在每個樹行中找最大值
• leetcode 637. 二叉樹的層平均值

這三道題，僅僅是加了一層的一些操作

• leetcode 116 填充每個節(jié)點的下一個右側(cè)
• leetcode 117 填充每個節(jié)點的下一個右側(cè)2

這兩個題對每一層的節(jié)點進行鏈接即可，兩道題目代碼一致

大家可以去順手解決這些題目，但是也要注意一下其他解法，把題目吃透。不要為了數(shù)目而刷題，好啦，今天的節(jié)目就到這里啦，我們下期見!

本文轉(zhuǎn)載自微信公眾號「袁廚的算法小屋」，可以通過以下二維碼關(guān)注。轉(zhuǎn)載本文請聯(lián)系袁廚的算法小屋公眾號。