面試官:說說你對樹的理解?相關的操作有哪些?
本文轉載自微信公眾號「JS每日一題」,作者灰灰。轉載本文請聯系JS每日一題公眾號。
一、是什么
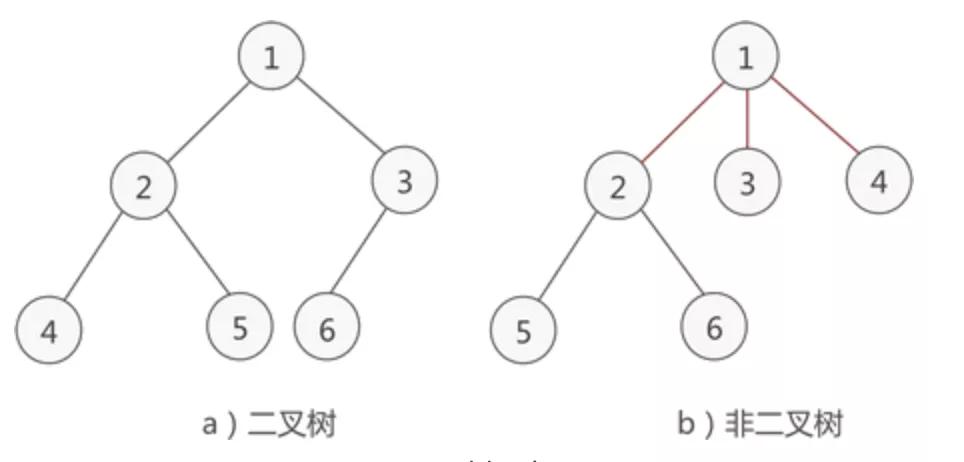
在計算機領域,樹形數據結構是一類重要的非線性數據結構,可以表示數據之間一對多的關系。以樹與二叉樹最為常用,直觀看來,樹是以分支關系定義的層次結構
二叉樹滿足以下兩個條件:
- 本身是有序樹
- 樹中包含的各個節點的度不能超過 2,即只能是 0、1 或者 2
如下圖,左側的為二叉樹,而右側的因為頭結點的子結點超過2,因此不屬于二叉樹:
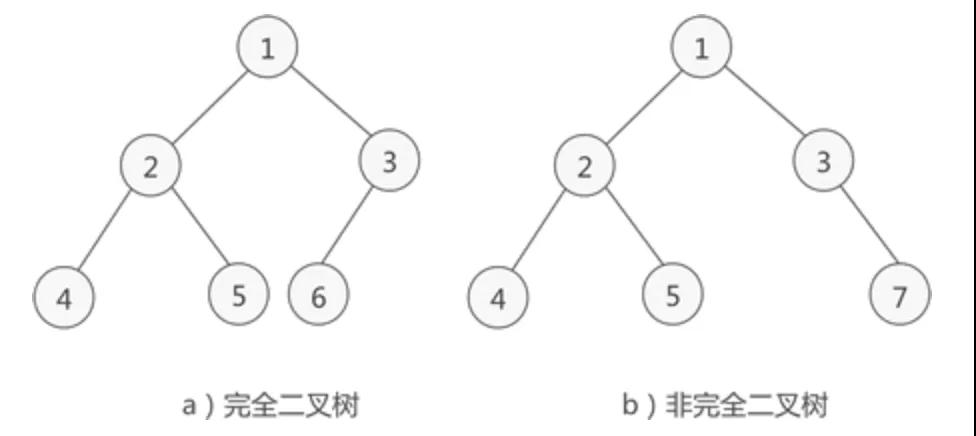
同時,二叉樹可以繼續進行分類,分成了滿二叉樹和完成二叉樹:
滿二叉樹:如果二叉樹中除了葉子結點,每個結點的度都為 2
完成二叉樹:如果二叉樹中除去最后一層節點為滿二叉樹,且最后一層的結點依次從左到右分布
二、操作
關于二叉樹的遍歷,常見的有:
- 前序遍歷
- 中序遍歷
- 后序遍歷
- 層序遍歷
前序遍歷
前序遍歷的實現思想是:
- 訪問根節點
- 訪問當前節點的左子樹
- 若當前節點無左子樹,則訪問當前節點的右子
根據遍歷特性,遞歸版本用代碼表示則如下:
- const preOrder = (root) => {
- if(!root){ return }
- console.log(root)
- preOrder(root.left)
- preOrder(root.right)
- }
如果不使用遞歸版本,可以借助棧先進后出的特性實現,先將根節點壓入棧,再分別壓入右節點和左節點,直到棧中沒有元素,如下:
- const preOrder = (root) => {
- if(!root){ return }
- const stack = [root]
- while (stack.length) {
- const n = stack.pop()
- console.log(n.val)
- if (n.right) {
- stack.push(n.right)
- }
- if (n.left) {
- stack.push(n.left)
- }
- }
- }
中序遍歷
前序遍歷的實現思想是:
- 訪問當前節點的左子樹
- 訪問根節點
- 訪問當前節點的右子
遞歸版本很好理解,用代碼表示則如下:
- const inOrder = (root) => {
- if (!root) { return }
- inOrder(root.left)
- console.log(root.val)
- inOrder(root.right)
- }
非遞歸版本也是借助棧先進后出的特性,可以一直首先一直壓入節點的左元素,當左節點沒有后,才開始進行出棧操作,壓入右節點,然后有依次壓入左節點,如下:
- const inOrder = (root) => {
- if (!root) { return }
- const stack = [root]
- let p = root
- while(stack.length || p){
- while (p) {
- stack.push(p)
- p = p.left
- }
- const n = stack.pop()
- console.log(n.val)
- p = n.right
- }
- }
后序遍歷
前序遍歷的實現思想是:
- 訪問當前節點的左子樹
- 訪問當前節點的右子
- 訪問根節點
遞歸版本,用代碼表示則如下:
- const postOrder = (root) => {
- if (!root) { return }
- postOrder(root.left)
- postOrder(root.right)
- console.log(n.val)
- }
后序遍歷非遞歸版本實際跟全序遍歷是逆序關系,可以再多創建一個棧用來進行輸出,如下:
- const preOrder = (root) => {
- if(!root){ return }
- const stack = [root]
- const outPut = []
- while (stack.length) {
- const n = stack.pop()
- outPut.push(n.val)
- if (n.right) {
- stack.push(n.right)
- }
- if (n.left) {
- stack.push(n.left)
- }
- }
- while (outPut.length) {
- const n = outPut.pop()
- console.log(n.val)
- }
- }
層序遍歷
按照二叉樹中的層次從左到右依次遍歷每層中的結點
借助隊列先進先出的特性,從樹的根結點開始,依次將其左孩子和右孩子入隊。而后每次隊列中一個結點出隊,都將其左孩子和右孩子入隊,直到樹中所有結點都出隊,出隊結點的先后順序就是層次遍歷的最終結果
用代碼表示則如下:
- const levelOrder = (root) => {
- if (!root) { return [] }
- const queue = [[root, 0]]
- const res = []
- while (queue.length) {
- const n = queue.shift()
- const [node, leval] = n
- if (!res[leval]) {
- res[leval] = [node.val]
- } else {
- res[leval].push(node.val)
- }
- if (node.left) { queue.push([node.left, leval + 1]) }
- if (node.right) { queue.push([node.right, leval + 1]) }
- }
- return res
- };
三、總結
樹是一個非常重要的非線性結構,其中二叉樹以二叉樹最常見,二叉樹的遍歷方式可以分成前序遍歷、中序遍歷、后序遍歷
同時,二叉樹又分成了完成二叉樹和滿二叉樹
參考文獻
https://baike.baidu.com/item/%E4%BA%8C%E5%8F%89%E6%A0%91
http://data.biancheng.net/view/27.html