論文地址：https://www.pnas.org/content/118/43/e2103091118

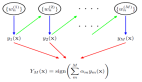
近日，賓夕法尼亞大學一團隊發表在頂級期刊《美國國家科學院院刊》上的一篇文章 [1] 提出了一種層間「剝離」 的分析模型，對上述問題給出了一種新思路。基于神經網絡強大的表達能力，該模型將網絡的部分層看作一個整體，將其輸出特征看作一個可以適應網絡訓練過程的優化變量，著重研究了特征與后繼層參數在網絡訓練中的相互作用。特別的，在僅剝離網絡最后一層的情形，神經網絡就被簡化為了下面的形式：

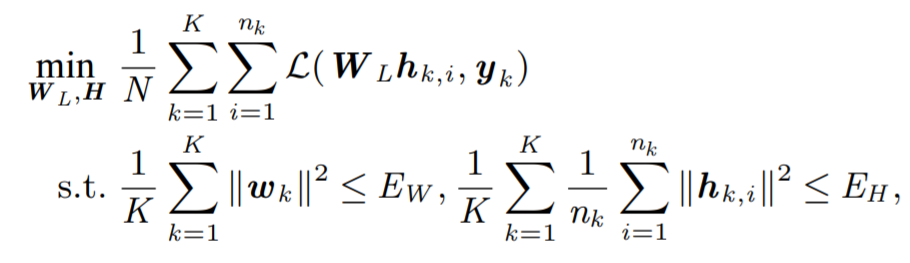
Figure 1 層間剝離模型的數學表達式。

作為這一全新分析視角的應用，文章對去年美國科學院院士 David Donoho 及其團隊提出的神經坍縮 (Neural Collapse) 現象 [2] 給出了嚴格的數學解釋。神經坍縮描述了一種當不同類的訓練樣本數量平衡時，在深層神經網絡的訓練過程的最終階段 (Terminal Phase of Training)，網絡最后一層的分類器和輸出特征會各自形成一種被稱為簡單等角緊框架(Simplex Equiangular Tight Frame) 的特殊幾何結構，并相互之間形成聯合的特殊現象。這一幾何結構中不同類的特征與分類器的夾角達到最大值，更難出現不同類之間相互混淆，因而神經坍縮現象解釋了為何深度神經網絡具有良好的泛化性能和魯棒性，對理解深度學習的優良性能有著重大意義。

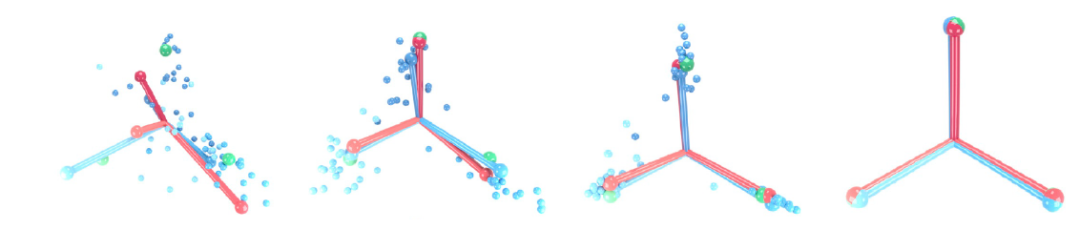
Figure 2 神經坍縮現象的圖示，紅色棍代表最后一層分類器的方向，藍色棍代表最后一層特征的平均值方向，藍色小球代表最后一層的特征向量，綠色小球代表簡單等角緊框架的方向，從左至右代表網絡訓練的過程，可以看到隨著訓練的進行，網絡最后一層的特征與分類器都逐漸收斂到了簡單等角緊框架的方向。

基于前面提到的層間剝離模型，文章中證明了在不同類的訓練樣本數量平衡時神經坍縮現象的全局最優性，從理論上揭示了為何神經坍縮現象在深層神經網絡中廣泛存在。更進一步的，文章考慮了不同類的訓練樣本數目不平衡的情況下的層間剝離模型，從理論分析中發現了一種全新的現象——非均衡坍縮(Minority Collapse)。非均衡坍縮指出，當訓練樣本中一些類的數目較多，而另一些類的數目較少時，神經坍縮中高度對稱的簡單等角緊框架結構被破壞，樣本數較多的類在損失函數中占據了主導性地位，從而其對應的最后一層的特征和分類器可以相互之間張成更大的角度，而樣本數較少的類則會被擠壓到一起，相互之間的夾角隨著樣本數目比例的減少而減小。文章中對非均衡坍縮現象給出了嚴格的數學刻畫，并經過大量的實驗驗證了這一現象的存在，且實驗結果與理論值嚴格符合。非均衡坍縮表明將深度學習工具用于可信人工智能時可能會引起不公平現象。值得注意的是，這個發現是深度學習中極少數完全由理論分析預測的。這個工作由賓夕法尼亞大學蘇煒杰和其團隊的方聰和何杭峰等人完成。值得注意的是，方聰博士近期已回國執教于北京大學智能科學系。

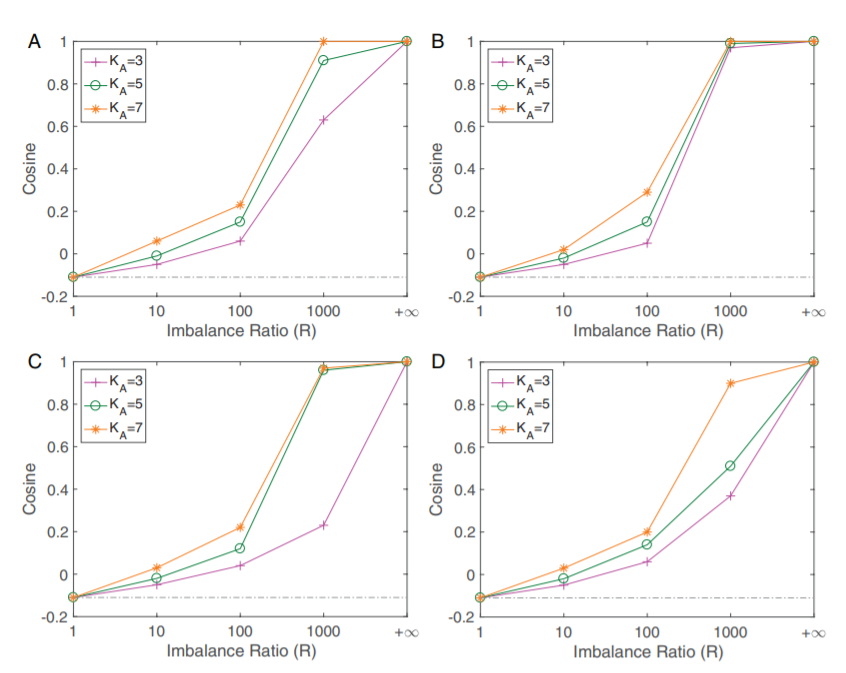
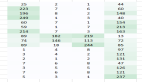
Figure 3深度神經網絡中的非均衡坍縮現象，橫坐標R代表類之間樣本數的比例，縱坐標代表樣本數較少的類的最后一層特征之間的方向的余弦值。可以看到隨著R從1增加到無窮大，這些樣本數較少的類的特征從神經坍縮中最大化兩兩之間夾角的方向逐漸被擠壓到相同的方向。ABCD四張圖分別是VGG和ResNet兩種網絡結構在Fashion-MNIST和CIFAR10兩個數據集上分別的結果。

訓練樣本中的不平衡帶來的公平性問題是機器學習領域長久以來的重要問題之一，常用的用來緩解這一問題的方法主要是重采樣 (resampling) 和重賦權 (reweighting) 兩種方法。在文章中，研究者通過層間剝離模型給出了這兩種方法有效性的理論保證：文章從數學上嚴格證明了利用重采樣和重賦權技術，深層神經網絡的對稱性可以被完全修復，神經坍縮中最大化不同類之間分類器和特征各自夾角的簡單等角緊框架結構將會重新出現，這就解釋了為何這兩種技術可以顯著提升網絡的泛化性能。

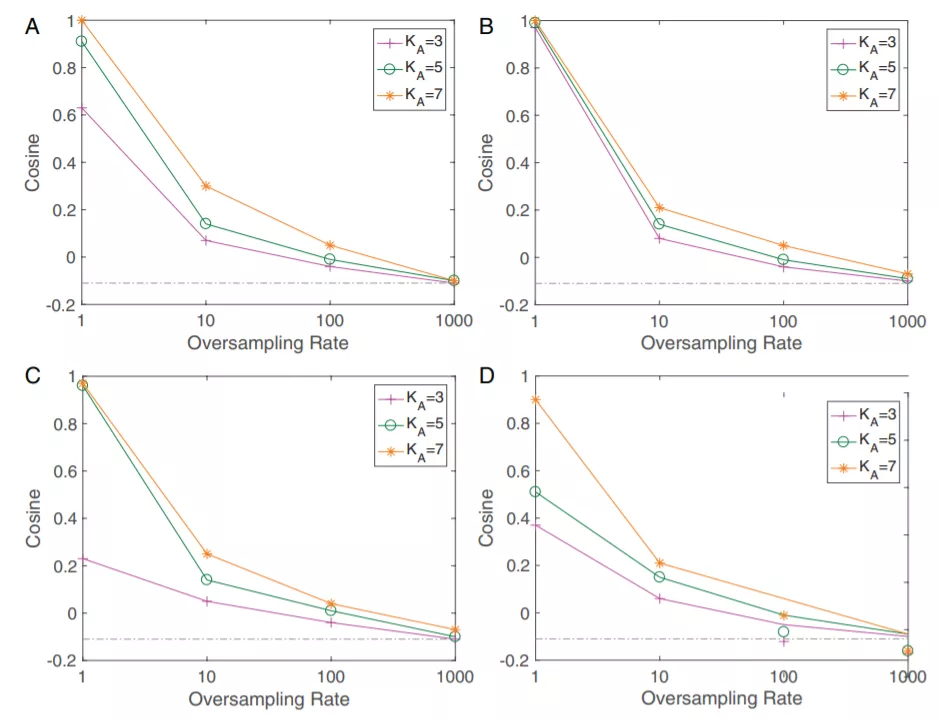
Figure 4 重采樣技術對于網絡最后一層對稱性的修復作用。可以看到隨著重采樣比例逐漸接近類之間的樣本數比例，數據集不平衡造成的對稱性破壞被重采樣逐漸修復，最終在兩個比例相等時完美地重現了神經坍縮地幾何結構。ABCD四張圖分別是VGG和ResNet兩種網絡結構在Fashion-MNIST和CIFAR10兩個數據集上分別的結果。

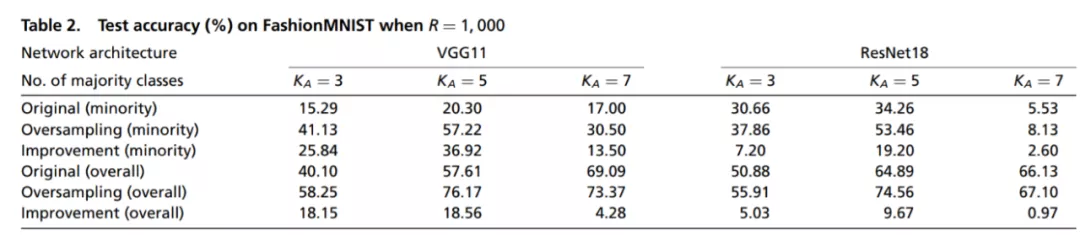
Figure 5 重采樣和原始訓練的泛化性能比較。可以看到在多種條件下，重采樣技術對網絡泛化性能的都有顯著提高。

在后續工作中，北大數院本科生冀文龍在蘇煒杰教授的指導下完成的一篇文章 [3] 基于層間剝離模型對神經坍縮現象做出了進一步的理論分析，文章提出了一種無約束層間剝離模型，去掉了對特征和參數的約束，研究了在更真實的條件下，網絡訓練中參數的漸進行為。文章指出了神經坍縮現象的出現與神經網絡的隱式正則化的關系，并在這一非凸問題上對于網絡損失函數的幾何景觀和梯度下降的訓練過程給出了嚴格的刻畫，更精確地解釋了梯度下降如何收斂到神經坍縮的幾何結構。

作為一種一般化的強有力分析手法，層間剝離模型為諸多深度學習理論問題提出了一種模塊化、剝離化的全新研究范式。進一步的研究方向包括如何利用多層層間剝離模型給出對神經網絡更精確的描述？在這種情況下是否存在更強的對稱性結果？如何將神經網絡的訓練與泛化納入到層間剝離模型的考慮范疇內？這一模型如何為其他當下流行的深度學習理論諸如信息瓶頸，隱式正則化，局部彈性提供全新的視角？相信在不久的未來，我們能夠看到層間剝離模型帶來更多令人振奮的結果。

References

[1] Cong Fang, Hangfeng He, Qi Long, and Weijie J. Su. "Exploring deep neural networks via layer-peeled model: Minority collapse in imbalanced training." Proceedings of the National Academy of Sciences 118, no. 43 (2021).

[2] Vardan Papyan, X. Y. Han, and David L. Donoho. "Prevalence of neural collapse during the terminal phase of deep learning training." Proceedings of the National Academy of Sciences 117, no. 40 (2020): 24652-24663.

[3] Wenlong Ji, Yiping Lu, Yiliang Zhang, Zhun Deng, and Weijie J. Su. "An Unconstrained Layer-Peeled Perspective on Neural Collapse." arXiv preprint arXiv:2110.02796 (2021).