周期性現(xiàn)象廣泛存在，深刻影響著人類社會(huì)和自然科學(xué)。作為最重要的基本特性之一，許多規(guī)律都顯式或隱式地包含周期性，例如，天文學(xué)中的行星運(yùn)動(dòng)、氣象學(xué)中的季節(jié)變化、生物學(xué)中的晝夜節(jié)律、經(jīng)濟(jì)學(xué)中的商業(yè)周期、物理學(xué)中的電磁波，以及數(shù)學(xué)運(yùn)算和邏輯推理等。

因此，在許多任務(wù)和場景中，人們希望對(duì)周期進(jìn)行建模，以便根據(jù)以往的經(jīng)驗(yàn)進(jìn)行推理。

盡管以 MLP 和 Transformer 為代表的基礎(chǔ)模型已經(jīng)取得了顯著的成功，但是它們卻在周期性建模方面存在潛在的缺陷。

即使面對(duì)簡單的正弦函數(shù)，現(xiàn)有基礎(chǔ)模型也難以理解其中的周期性規(guī)律，在外推時(shí)表現(xiàn)出完全失控的狀態(tài)，未能有效捕捉到周期性現(xiàn)象的本質(zhì)。

為此，北京大學(xué)李戈教授的團(tuán)隊(duì)提出了一種新型網(wǎng)絡(luò)架構(gòu)FAN（Fourier Analysis Networks）。通過引入傅里葉級(jí)數(shù)的思想，F(xiàn)AN能夠?qū)⒅芷谛孕畔⒅苯忧度刖W(wǎng)絡(luò)的結(jié)構(gòu)中，使模型更自然地捕捉和理解數(shù)據(jù)中的周期性模式。

實(shí)驗(yàn)表明，F(xiàn)AN不僅在周期性建模上的表現(xiàn)顯著優(yōu)于現(xiàn)有模型，而且在符號(hào)公式表示、時(shí)間序列預(yù)測和語言建模等實(shí)際任務(wù)中也同樣表現(xiàn)出色，超過了Transformer等主流模型。

論文鏈接：https://arxiv.org/pdf/2410.02675.pdf

代碼鏈接：https://github.com/YihongDong/FAN

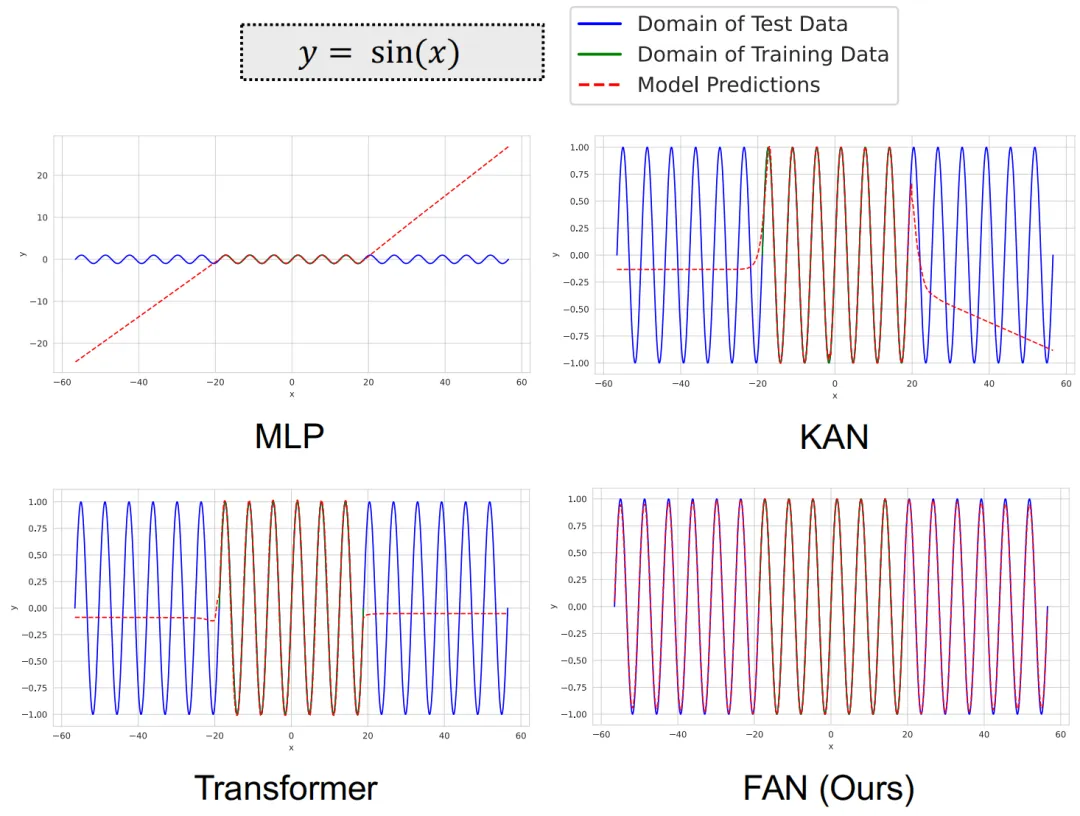
圖1 不同基礎(chǔ)模型在其訓(xùn)練數(shù)據(jù)域內(nèi)外對(duì)正弦函數(shù)的表現(xiàn)，其中x為標(biāo)量

研究者認(rèn)為，許多實(shí)際任務(wù)都顯式或者隱式地包含潛在的周期性特征，良好的周期性建模對(duì)于提升模型在這些任務(wù)上的表現(xiàn)是必要的，而現(xiàn)有基礎(chǔ)模型嚴(yán)重依賴數(shù)據(jù)驅(qū)動(dòng)的優(yōu)化方式，缺少明確的機(jī)制來理解數(shù)據(jù)中的根本原理。

FAN的意義在于，它提供了一種全新的范式來有效地建模周期性，能夠無縫替換傳統(tǒng)MLP，同時(shí)減少參數(shù)量和計(jì)算量，填補(bǔ)了當(dāng)前基礎(chǔ)模型在周期性建模上的缺陷，并展示出廣泛的應(yīng)用潛力。

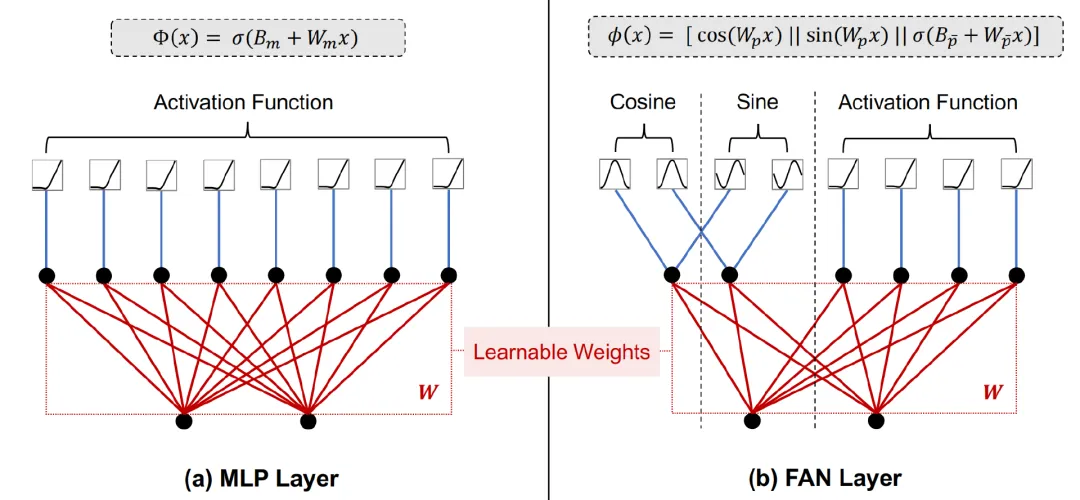
圖2 MLP Layer和FAN Layer的示例

本文的通訊作者是北京大學(xué)計(jì)算機(jī)學(xué)院長聘教授、教育部長江學(xué)者李戈。第一作者：董益宏，北京大學(xué)計(jì)算機(jī)學(xué)院22級(jí)博士生，曾在ISSTA、FSE、ACL、NeurIPS、TOSEM等 CCF-A類/SCI一區(qū)國際頂級(jí)會(huì)議和期刊上發(fā)表11篇學(xué)術(shù)論文。

FAN的實(shí)現(xiàn)細(xì)節(jié)

北大研究團(tuán)隊(duì)首先構(gòu)建一個(gè)簡單神經(jīng)網(wǎng)絡(luò)來建模傅里葉級(jí)數(shù)，然后在此基礎(chǔ)上設(shè)計(jì)了FAN網(wǎng)絡(luò)架構(gòu)。

為構(gòu)建一個(gè)簡單的神經(jīng)網(wǎng)絡(luò)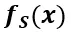表示函數(shù)的傅里葉級(jí)數(shù)展開，我們可以將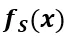表示為：

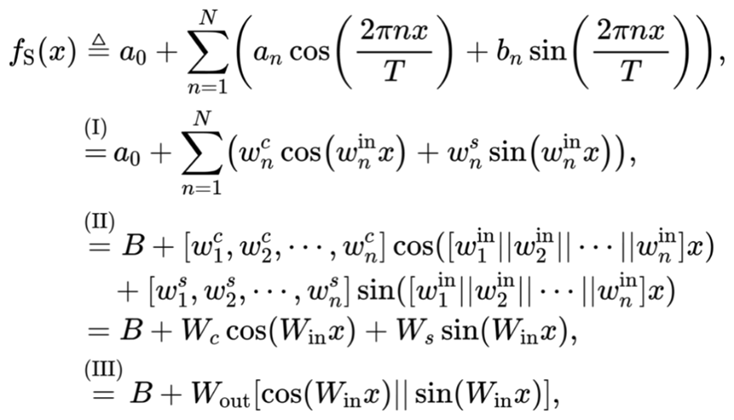
其中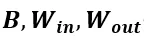是可學(xué)習(xí)參數(shù)，(I) 根據(jù)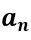和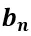通過定積分計(jì)算，(II) 和 (III) 是矩陣運(yùn)算的等價(jià)形式，[·||·] 和 [·, ·] 分別表示沿第一維度和第二維度的連接。

為了充分利用深度學(xué)習(xí)的優(yōu)勢，我們可以堆疊上述網(wǎng)絡(luò)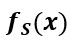形成深度神經(jīng)網(wǎng)絡(luò)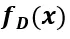，其中第i層表示為。

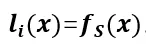因此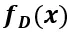，可以表示為：

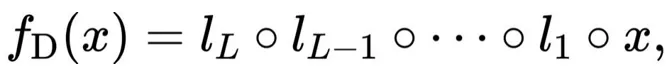
其中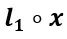表示左側(cè)函數(shù)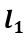作用于右側(cè)輸入x，即。

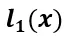然而，我們發(fā)現(xiàn)直接堆疊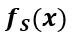會(huì)導(dǎo)致模型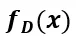的主要參數(shù)集中于學(xué)習(xí)角頻率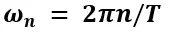，從而忽略了傅里葉系數(shù)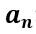和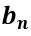的學(xué)習(xí)，如下所示：

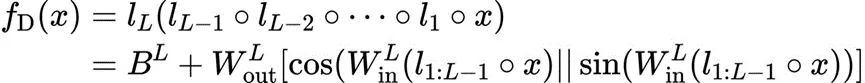
其中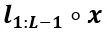定義為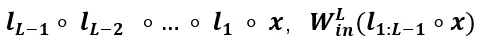用于近似角頻率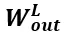，用于近似傅里葉系數(shù)。

因此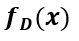，擬合傅里葉系數(shù)的能力與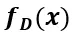的深度無關(guān)，這是一個(gè)不理想的結(jié)果。

為了應(yīng)對(duì)這一問題，研究團(tuán)隊(duì)根據(jù)以下原則設(shè)計(jì)了FAN：

1. FAN 表示傅里葉系數(shù)的能力應(yīng)與其深度正相關(guān)；

2. 任何隱藏層的輸出都可以通過后續(xù)層使用傅里葉級(jí)數(shù)來建模周期性。

第一個(gè)原則通過利用FAN的深度增強(qiáng)了其周期性建模的表現(xiàn)力，而第二個(gè)原則確保FAN中間層的特征可用于執(zhí)行周期性建模。

假設(shè)我們將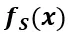解耦為：

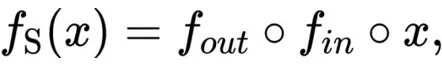
其中，

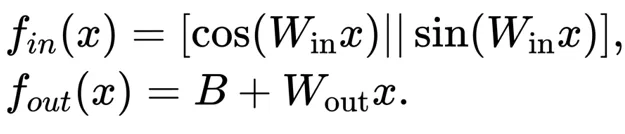
為了滿足這兩個(gè)原則，F(xiàn)AN的中間層輸入需要同時(shí)使用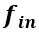和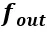而不是依次應(yīng)用它們。

最終，F(xiàn)AN 基于此設(shè)計(jì)，其FAN層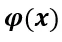定義如下：

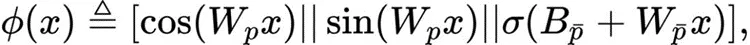
其中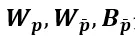是可學(xué)習(xí)參數(shù)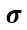，表示激活函數(shù)。

整個(gè)FAN定義為FAN Layer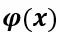的堆疊：

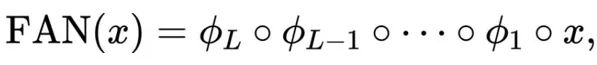
其中，

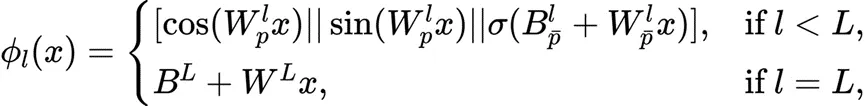
FAN的性能表現(xiàn)

周期建模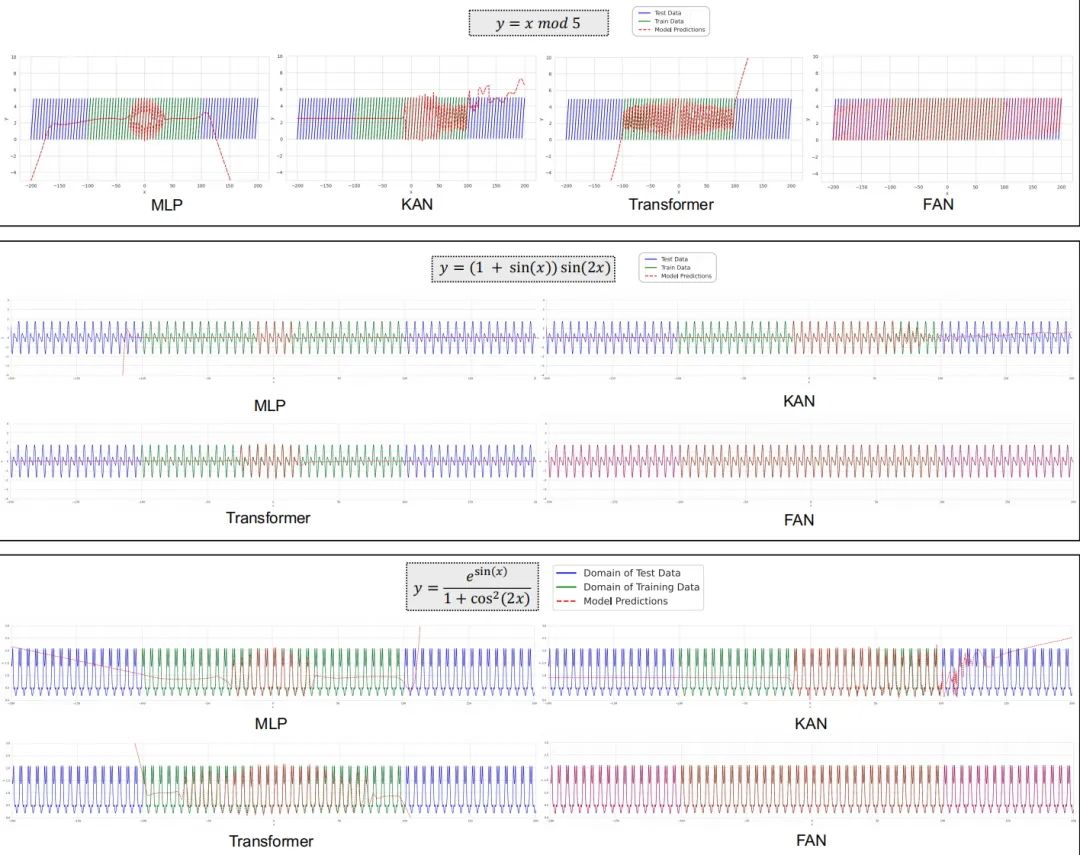 

圖3 FAN在周期性建模中的表現(xiàn)與 MLP、KAN 和 Transformer 相比，其中綠線表示訓(xùn)練數(shù)據(jù)域內(nèi)的測試數(shù)據(jù)，而藍(lán)線表示訓(xùn)練數(shù)據(jù)域外的測試數(shù)據(jù)

圖3展示了FAN和其他模型在周期性建模中的表現(xiàn)。結(jié)果表明，現(xiàn)有的神經(jīng)網(wǎng)絡(luò)（包括 MLP、KAN 和 Transformers）在建模周期性方面表現(xiàn)出明顯的不足。盡管它們試圖擬合這些周期函數(shù)，但其內(nèi)在能力限制了它們在大范圍周期性上的性能表現(xiàn)。

相比之下，F(xiàn)AN在所有這些周期性建模任務(wù)中都明顯優(yōu)于基線。更值得一提的是，F(xiàn)AN在訓(xùn)練數(shù)據(jù)域內(nèi)和域外的測試數(shù)據(jù)上都表現(xiàn)得非常出色，表明它能夠真正理解周期性的深刻原理并對(duì)其進(jìn)行精準(zhǔn)建模，而不僅僅是記住訓(xùn)練數(shù)據(jù)。

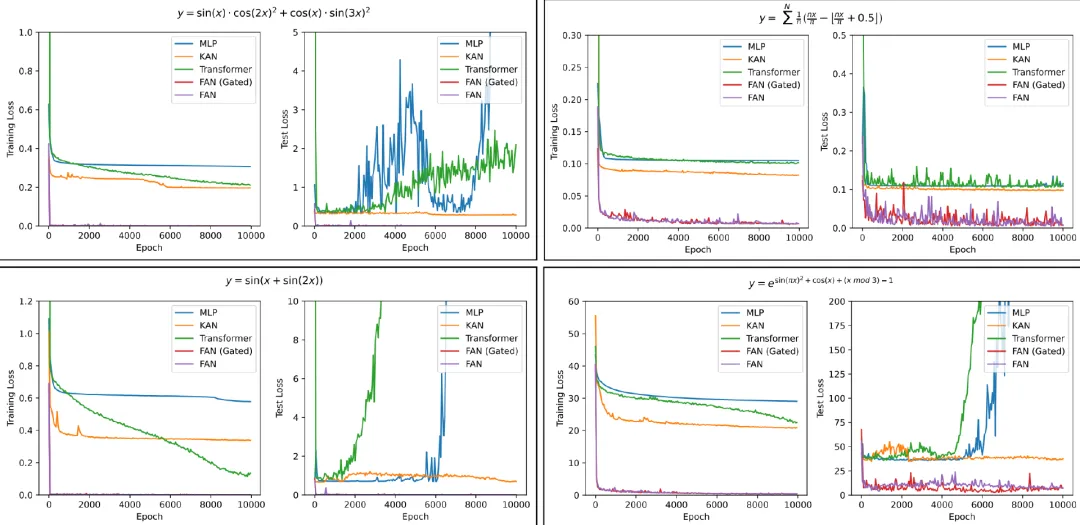
圖4 不同模型在學(xué)習(xí)復(fù)雜周期函數(shù)任務(wù)上的訓(xùn)練和測試損失比較

研究團(tuán)隊(duì)還分析了不同模型在學(xué)習(xí)復(fù)雜周期函數(shù)任務(wù)上的訓(xùn)練過程，如圖4所示，結(jié)果如下：

1. FAN在收斂速度和最終效果方面都遠(yuǎn)遠(yuǎn)超過其他模型；

2. 與FAN相比，F(xiàn)AN (Gated) 通常可以實(shí)現(xiàn)更快的收斂，但最終性能仍然相當(dāng)；

3. 隨著訓(xùn)練輪數(shù)的增加，雖然其他模型的訓(xùn)練損失變得穩(wěn)定或逐漸減少，但它們的建模可能與測試數(shù)據(jù)的分布有很大差異，導(dǎo)致測試損失急劇增加。這一現(xiàn)象進(jìn)一步證明了這些模型在捕捉周期性方面的缺陷。

符號(hào)公式表示

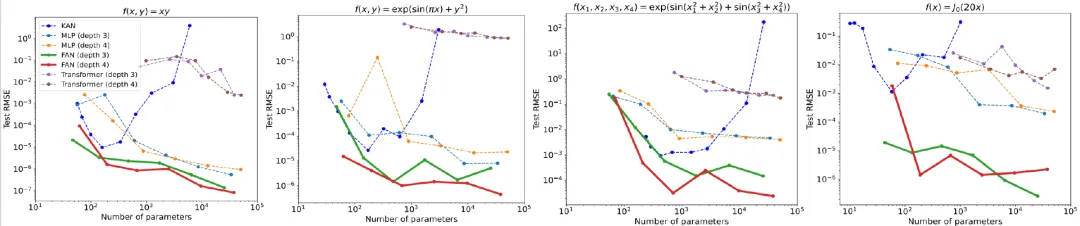
圖5 不同模型在符號(hào)公式表示任務(wù)中不同參數(shù)量的表現(xiàn)

從不同模型應(yīng)用于數(shù)學(xué)和物理學(xué)中四個(gè)常見函數(shù)的表現(xiàn)中可以觀察到，雖然 KAN 在參數(shù)數(shù)量較少時(shí)能與FAN相媲美，但隨著參數(shù)數(shù)量的增加，其性能會(huì)顯著下降。

相反，隨著參數(shù)數(shù)量的增加，F(xiàn)AN擬合這些函數(shù)始終優(yōu)于其他基線，包括 MLP、KAN 和 Transformer，盡管這些函數(shù)中的許多只是部分周期性的或完全非周期性的。

這些結(jié)果表明，F(xiàn)AN不僅增強(qiáng)了對(duì)周期性的建模能力，同時(shí)也沒有損害擬合非周期性函數(shù)的能力。

時(shí)間序列預(yù)測

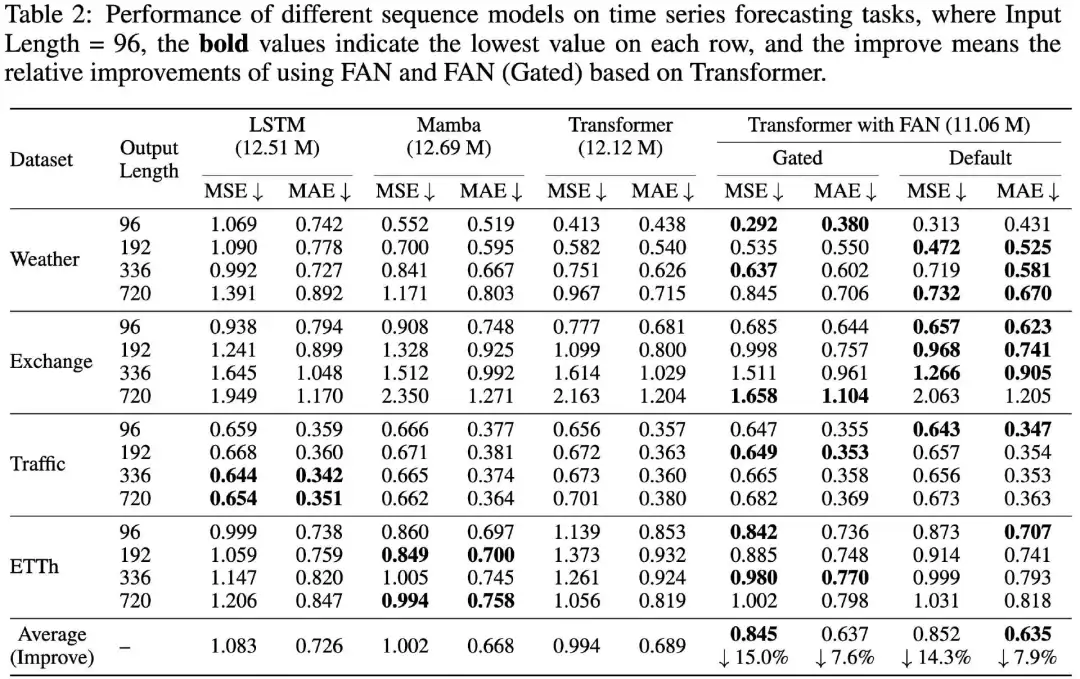
如表2 所示，研究團(tuán)隊(duì)在四個(gè)公共數(shù)據(jù)集上比較了結(jié)合FAN的Transformer 和其他序列模型在時(shí)間序列預(yù)測任務(wù)上的表現(xiàn)。在大多數(shù)情況下，與 LSTM、Mamba 和標(biāo)準(zhǔn) Transformer 相比，結(jié)合FAN和FAN（Gated）的Transformer 在這些任務(wù)上取得了最佳性能。

它們相對(duì)于標(biāo)準(zhǔn) Transformer 的改進(jìn)是顯著的，平均相對(duì)改進(jìn)范圍為14.3%-15.0%的 MSE和7.6%-7.9%的MAE。

這些結(jié)果表明，在神經(jīng)網(wǎng)絡(luò)中加入顯式周期模式編碼可以提高實(shí)際應(yīng)用中的時(shí)間序列預(yù)測性能。

語言建模

探究者報(bào)告了不同序列模型在四種情緒分析數(shù)據(jù)集上的性能比較，如表3所示。

可以發(fā)現(xiàn)，結(jié)合FAN和FAN（Gated）的Transformer與標(biāo)準(zhǔn) Transformer 和其他序列模型（例如 LSTM 和 Mamba）相比表現(xiàn)出明顯優(yōu)越的性能，尤其是在 IMDB、Sentiment140 和 Amazon Reviewers 數(shù)據(jù)集上的零樣本跨領(lǐng)域表現(xiàn)。

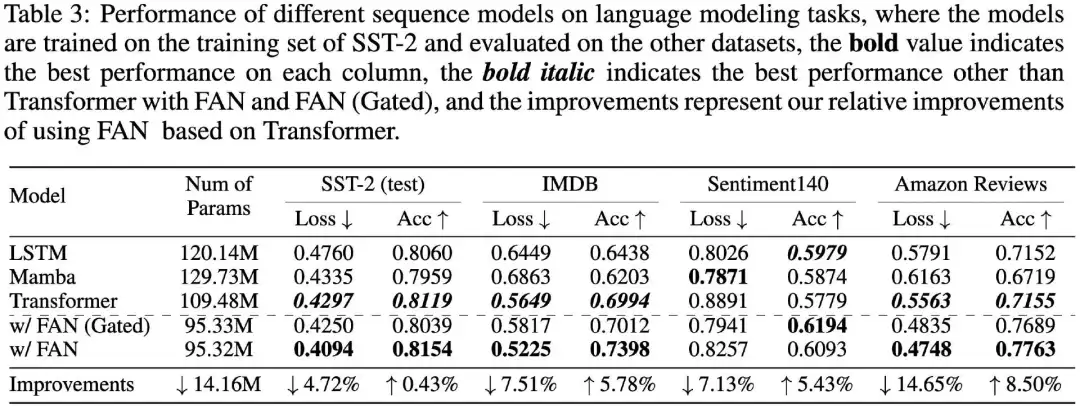
結(jié)合FAN的 Transformer 在損失和準(zhǔn)確度方面分別實(shí)現(xiàn)了最14.65%和8.50%的相對(duì)改進(jìn)，同時(shí)將參數(shù)數(shù)量減少了約 14.16M。結(jié)果表明周期性建模在跨領(lǐng)域語言建模和情緒分析任務(wù)上具有提高有效性和泛化的潛力。

FAN的表達(dá)能力和應(yīng)用范圍

FAN在理論上具有與MLP相同的表達(dá)能力，因?yàn)樗沧裱ㄓ媒贫ɡ恚@確保了其函數(shù)近似能力。不同的是，F(xiàn)AN通過明確納入周期性，引入了重要的功能增強(qiáng)，這是傳統(tǒng)MLP所不具備的。

FAN的這一設(shè)計(jì)，不僅全面繼承了MLP的既有優(yōu)勢，還增強(qiáng)了其捕獲數(shù)據(jù)周期性特征的能力。因此，F(xiàn)AN可以作為MLP的有力替代品。

當(dāng)然，F(xiàn)AN的實(shí)用性不僅限于明確需要周期性建模的任務(wù)，在更廣泛的應(yīng)用中也展現(xiàn)出強(qiáng)大的適用性。研究團(tuán)隊(duì)通過一系列現(xiàn)實(shí)世界任務(wù)的實(shí)驗(yàn)證明，如符號(hào)公式表示、時(shí)間序列預(yù)測和語言建模等，F(xiàn)AN的表現(xiàn)明顯優(yōu)于MLP和其他基線模型。

事實(shí)上，許多看似與周期性無直接關(guān)聯(lián)的機(jī)器學(xué)習(xí)任務(wù)，如數(shù)學(xué)運(yùn)算和邏輯推理，實(shí)際上也可能隱藏著周期性。

如果神經(jīng)網(wǎng)絡(luò)缺乏針對(duì)周期性特征進(jìn)行建模的能力，則可能會(huì)損害其學(xué)習(xí)效率。

從更深層次的角度來看，周期性不僅僅是一種數(shù)據(jù)特征，還反映了一種規(guī)律或知識(shí)，即允許抽象的規(guī)則和原理在不同上下文之間轉(zhuǎn)移和重用。

總結(jié)來看，F(xiàn)AN與MLP相比，不僅增強(qiáng)了周期性建模能力，且參數(shù)量和計(jì)算量更少，有望成為基礎(chǔ)模型的關(guān)鍵組成部分。

未來，北大研究團(tuán)隊(duì)將進(jìn)一步擴(kuò)大FAN的應(yīng)用范圍，增強(qiáng)其作為基礎(chǔ)模型組件的表現(xiàn)，持續(xù)推動(dòng)基礎(chǔ)模型的技術(shù)進(jìn)步與創(chuàng)新發(fā)展。