單鏈表的常見操作比較多，而且有些操作比較有技巧，本文就來聊聊這些不容易想到操作。

單鏈表倒數(shù)第 k 個(gè)節(jié)點(diǎn)

單鏈表正向第 k 個(gè)節(jié)點(diǎn)很容易獲得，直接一個(gè) for 循環(huán)遍歷一遍鏈表就能得到，但是如果是逆向第 k 個(gè)節(jié)點(diǎn)，也就是倒數(shù)第 k 個(gè)節(jié)點(diǎn)呢 ?

你也許很快就想到了，逆向第 k 個(gè)節(jié)點(diǎn)相當(dāng)于正向第 n - k 個(gè)節(jié)點(diǎn), 這里的 n 是鏈表長度，對于單鏈表來說，需要遍歷一遍鏈表才能計(jì)算出 n 的值，然后再次遍歷 n - k 個(gè)節(jié)點(diǎn), 才最終獲得鏈表倒數(shù)第 k 個(gè)節(jié)點(diǎn)。

上面整個(gè)過程總共遍歷了 n + n - k 個(gè)節(jié)點(diǎn)，能否只遍歷 n 個(gè)節(jié)點(diǎn)就能得到倒數(shù)第 n 個(gè)節(jié)點(diǎn)呢 ?

答案是肯定的，這種解法稱作 雙指針法，它比較巧妙，如果以前沒接觸過過的話，不容易想到，下面就來詳細(xì)介紹它。

假如 k = 2, 現(xiàn)在讓指針 p1 指向 head 節(jié)點(diǎn)，然后移動 k 步，結(jié)果如下圖：

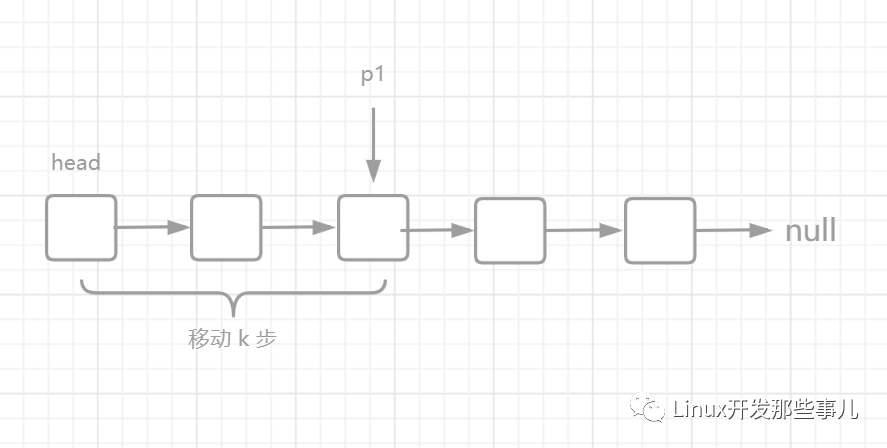
此時(shí)，如果 p1 再移動 n - k 步就到達(dá)鏈表結(jié)尾的 null 節(jié)點(diǎn)了。

再用一個(gè)指針 p2 指向 head 節(jié)點(diǎn)，指針 p1 和 p2 的指向如下圖所示：

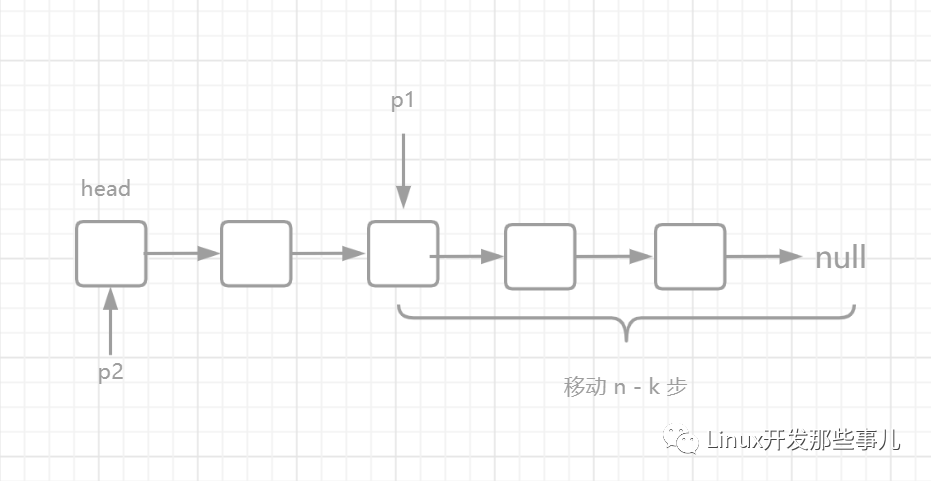
最后，指針 p1 和 p2 同時(shí)向前移動，直到 p1 到達(dá)鏈表結(jié)尾的 null 節(jié)點(diǎn)，此時(shí)兩個(gè)指針的指向如下圖所示：

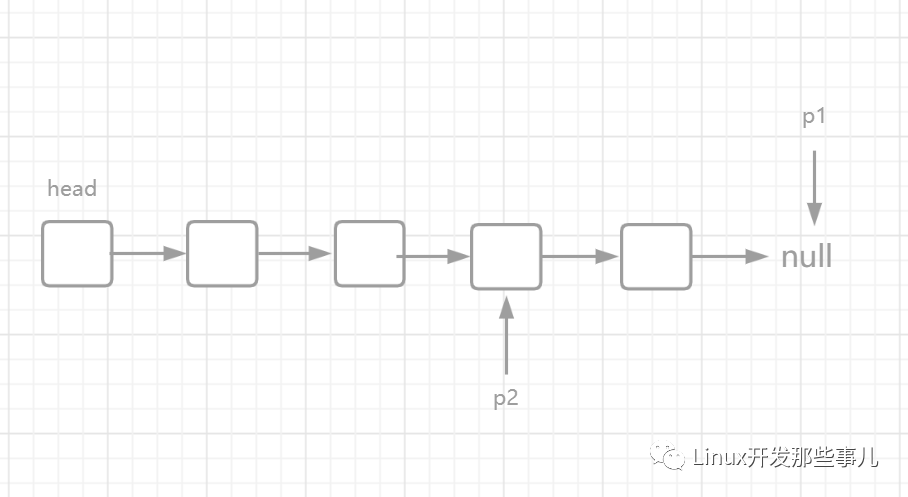
當(dāng) p1 到達(dá) null 節(jié)點(diǎn)時(shí)，p2 走了 n - k 步，也就是倒數(shù)第 k 個(gè)節(jié)點(diǎn)。

這樣，利用 p1 和 p2 兩個(gè)指針，只需要遍歷一遍鏈表就能得到倒數(shù)第 k 個(gè)節(jié)點(diǎn)，也即 p2 指向的節(jié)點(diǎn)。

在整個(gè)過程中，使用了兩個(gè)指針，所以這個(gè)技巧稱作 雙指針法，很多鏈表相關(guān)的算法題都可以用這個(gè)技巧解決，理解了這個(gè)套路，以后再遇到類似的問題就可以手到擒來了。

好了，流程講完了，下面給出完整代碼供大家參考：

// 單鏈表節(jié)點(diǎn)結(jié)構(gòu)
struct ListNode
{
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *pnext) : val(x), next(pnext) {}
};
// 返回單鏈表倒數(shù)第 k 個(gè)節(jié)點(diǎn)
ListNode *findFromEnd(ListNode *head, int k)
{
    if(nullptr == head || k <= 0) return nullptr;
    ListNode *p1 = head;
    // p1 指針先移動 k 步
    int step = 0;
    while (step < k && nullptr != p1)
    {
        p1 = p1->next;
        ++step;        
    }
    //p1 移動的步數(shù)小于 k, 表示鏈表長度小于 k
    //因此鏈表不存在倒數(shù)第 k 個(gè)節(jié)點(diǎn)
    if (step < k) return nullptr;
    //p1 和 p2 同時(shí)移動，直到 p1 到達(dá)尾節(jié)點(diǎn)的下一節(jié)點(diǎn)
    ListNode *p2 = head;
    while (nullptr != p1)
    {
        p2 = p2->next;
        p1 = p1->next;
    }
    return p2;
}

單鏈表中點(diǎn)

想得到單鏈表的中點(diǎn)，首先想到的是先得到鏈表的長度 n，然后從鏈頭開始往前走，每走一步，計(jì)數(shù)就加一，直到計(jì)數(shù)達(dá)到鏈表長度的一半兒 n / 2，此時(shí)所在的節(jié)點(diǎn)即為鏈表的中點(diǎn)了。

但是這個(gè)方法需要先遍歷整個(gè)鏈表，然后再從鏈表頭遍歷到鏈表的中間節(jié)點(diǎn)，整個(gè)過程共遍歷了 n + n / 2 個(gè)節(jié)點(diǎn)。

這里介紹一種方法，只需要遍歷 n 個(gè)節(jié)點(diǎn)就可以得到鏈表的中間節(jié)點(diǎn)。

我們讓指針 p1 和 p2 都指向 head 節(jié)點(diǎn)，兩個(gè)指針同時(shí)向前移動，p1 每次向前走兩步，p2 每次向前走一步，這樣，當(dāng) p1達(dá)到鏈表尾節(jié)點(diǎn)時(shí)，p2 剛好到達(dá)鏈表的中間節(jié)點(diǎn)。

在這個(gè)過程中，p1 指針每次走兩步，稱為快指針，p2 指針每次走一步，稱為慢指針，所以，這個(gè)小技巧叫做 快慢指針。

根據(jù)上面的思路，我們就可以寫出算法的實(shí)現(xiàn)代碼了。

// 單鏈表節(jié)點(diǎn)結(jié)構(gòu)
struct ListNode
{
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *pnext) : val(x), next(pnext) {}
};
// 返回單鏈表中間節(jié)點(diǎn)
ListNode * middleNode(ListNode *head)
{
    if(nullptr == head) return nullptr;
    //快指針和慢指針初始都指向head
    ListNode *pslow = head;
    ListNode *pfast = head;
    while (nullptr != pfast && nullptr != pfast->next)
    {
        //每次快指針走兩步，慢指針走一步
        //當(dāng)快指針的下一個(gè)節(jié)點(diǎn)為 null時(shí)
        //表示快指針達(dá)到了末尾節(jié)點(diǎn),此時(shí)退出循環(huán)
        pfast = pfast->next->next;
        pslow = pslow->next;
    }
    return pslow;    
}

需要說明一點(diǎn)，如果單鏈表長度為偶數(shù)，也就是中間節(jié)點(diǎn)有兩個(gè)，上面的解法返回的是靠后一個(gè)節(jié)點(diǎn)。

例如: 單鏈表 1 -> 2 -> 3 -> 4 -> 5 -> 6，長度為 6，它的中間節(jié)點(diǎn)是 3 和 4，那么，用上面的解法得到的中間節(jié)點(diǎn)是 4 而不是 3。

鏈表是否包含環(huán)

如下圖所示，圖中是一個(gè)長度為5的鏈表，最后一個(gè)節(jié)點(diǎn)指向了第三個(gè)節(jié)點(diǎn)，構(gòu)成了一個(gè)環(huán)。

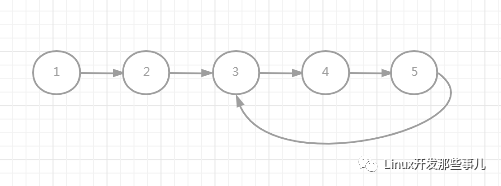
給你一個(gè)單鏈表的頭節(jié)點(diǎn)，判斷該鏈表是否含有環(huán)。

如何判斷單鏈表存在環(huán)呢 ?我們可以借用 單鏈表的中點(diǎn) 問題的思路。

快慢指針同從頭節(jié)點(diǎn)同時(shí)向前移動，在沒有環(huán)的單鏈表中，它們依次達(dá)到尾節(jié)點(diǎn)，但對于有環(huán)的鏈表來說，快慢指針最后會一直在環(huán)中移動，永遠(yuǎn)停不下來。

由于兩個(gè)指針一塊一慢，并且快指針每次比慢指針多走一步，因此，快指針總有一天會追上慢指針，此時(shí)它倆就指向同一個(gè)節(jié)點(diǎn)，明白了這一點(diǎn)，就有辦法判斷單鏈?zhǔn)欠翊嬖诒憝h(huán)了，具體做法如下：

初始時(shí)，快慢指針都指向頭節(jié)點(diǎn)，它們同時(shí)向前移動，快指針每次走兩步，慢指針每次走一步，當(dāng)快指針和慢指針相等時(shí)，說明鏈表有環(huán)，如果快指針的下一個(gè)節(jié)點(diǎn)是 null 節(jié)點(diǎn)，表示鏈表沒有環(huán)。

根據(jù)上面的思路，就可以寫出實(shí)現(xiàn)代碼了。

//返回單鏈表是否存在環(huán)
bool hasCycle(ListNode *head)
{
    if(nullptr == head) return false;
    //快指針和慢指針初始都指向head
    ListNode *pslow = head;
    ListNode *pfast = head;
    while (nullptr != pfast && nullptr != pfast->next)
    {
        //快指針每次走兩步，慢指針每次走一步
        //當(dāng)快指針的下一個(gè)節(jié)點(diǎn)為 null時(shí)
        //表示快指針達(dá)到了末尾節(jié)點(diǎn)
        pfast = pfast->next->next;
        pslow = pslow->next;
        if (pfast == pslow)
        {
            return true;
        }
    }
    return false;
}

鏈表環(huán)的起始節(jié)點(diǎn)

我們再深入下，既然解決了鏈表是否有環(huán)的問題，那能不能知道環(huán)的起始節(jié)點(diǎn)呢 ?

比如: 對于下圖中的鏈表來說，環(huán)的起始節(jié)點(diǎn)是 3。

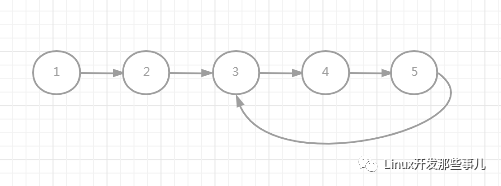
解決的方法依然是使用快慢指針，快指針每次走兩步，慢指針每次走一步。

下圖是一個(gè)簡易的環(huán)形鏈表圖，其中 A 為鏈表頭節(jié)點(diǎn)，B 為環(huán)的起始節(jié)點(diǎn)，C為 快指針和慢指針在環(huán)中相遇的節(jié)點(diǎn)(至于快指針和慢指針為什么一定會在環(huán)中相遇，在上一小節(jié)有解釋，這里不在贅述了)。

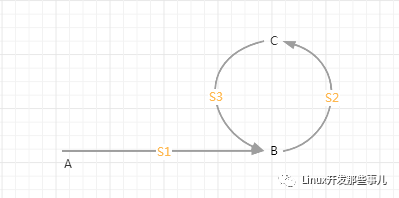
A 到 B 的距離是 S1。

B 到 C 的距離是 S2。

C 到 B 的距離是 S3。

假設(shè)，當(dāng)快指針和慢指針在 C點(diǎn)相遇時(shí)，快指針已經(jīng)繞著環(huán)走了 n 圈，則相遇時(shí)各自走過的路程如下：

快指針: S1 + n * ( S2 + S3 ) + S2。

慢指針：S1 + S2。

由于快指針走過的路程是慢指針的 2 倍，則有：

S1 + n * ( S2 + S3 ) = 2 * (S1 + S2)

簡化下上面的等式可以得到:

S1 = (n - 1) * (S2 + S3) + S3

S2 + S3 剛好是環(huán)的長度，所以，上面的結(jié)果可以理解為，從 A 到 B 的距離，等于從相遇點(diǎn) C 出發(fā)，繞著環(huán)走 n - 1圈 ( 此時(shí)會回到 C 點(diǎn) ) ，然后再走 S3 就到達(dá)了 B 點(diǎn)，也即環(huán)的起始點(diǎn)。

因此，當(dāng)快慢指針相遇后，再額外使用一個(gè)指針指向鏈表頭節(jié)點(diǎn)，然后這個(gè)額外指針和慢指針同時(shí)移動，它們最終一定會在環(huán)的起始節(jié)點(diǎn)相遇。

搞明白了上面的推理過程之后，實(shí)現(xiàn)代碼直接在 鏈表是否存在環(huán) 那一小節(jié)的基礎(chǔ)上稍作修改即可，具體的代碼如下：

//返回單鏈表環(huán)的起始節(jié)點(diǎn)
ListNode *entrynodeInLoop(ListNode *head)
{
    if (nullptr == head || nullptr == head->next)
        return nullptr;
    ListNode *pslow = head;  //慢指針
    ListNode *pfast = head;  //快指針
    ListNode *ppoint = nullptr;//指向快慢指針相遇時(shí)的節(jié)點(diǎn)
    while (nullptr != pfast && nullptr != pfast->next)
    {
        pslow = pslow->next;
        pfast = pfast->next->next;
        if (pslow == pfast)
        {
            ppoint = pslow;
            break;
        }
    }
    //相遇節(jié)點(diǎn)為null,表示沒有環(huán)
    if (nullptr == ppoint) return nullptr;
    pslow = head;  //慢指針指向頭節(jié)點(diǎn)
    while (pslow != ppoint)
    {
        pslow = pslow->next;
        ppoint = ppoint->next;
    }
    return ppoint;
}

其實(shí)，鏈表是否有環(huán) 以及 鏈表環(huán)的起始節(jié)點(diǎn) 還有一種比較直觀的求解方法。

額外增加一個(gè)記錄節(jié)點(diǎn)指針的集合，然后從頭節(jié)點(diǎn)開始往前遍歷，每經(jīng)過一個(gè)節(jié)點(diǎn)，查詢集合中是否已存在該節(jié)點(diǎn)，如果不存在，節(jié)點(diǎn)指針加入到集合中，如果存在，則表示該節(jié)點(diǎn)就是環(huán)的入口節(jié)點(diǎn)。

這種方法比較好理解，但是它的空間復(fù)雜度是 O(N), 時(shí)間復(fù)雜度跟 快慢指針 相同，這里也給出實(shí)現(xiàn)代碼供參考。

//返回鏈表環(huán)的起始節(jié)點(diǎn)
ListNode *entrynodeInLoop(ListNode *head)
{
    if(nullptr == head) return nullptr;
    //鏈表節(jié)點(diǎn)的集合
    unordered_set<ListNode*> setnode;
    ListNode *p = head;
    while (nullptr != p)
    {
        auto iter = setnode.find(p);
        if( iter != setnode.end())
        {
            //集合中找到了相同的節(jié)點(diǎn)
            //此節(jié)點(diǎn)即為環(huán)的入口
            return p;
        }
        //節(jié)點(diǎn)不在集合中，則加入集合
        setnode.insert(p);
        //移動到下一個(gè)節(jié)點(diǎn)
        p = p->next;
    }
    //不存在環(huán)，返回 nullptr
    return nullptr;    
}

兩個(gè)鏈表是否相交

給你兩個(gè)鏈表的頭節(jié)點(diǎn)，如果這兩個(gè)鏈表相交，則返回相交的節(jié)點(diǎn)，如果沒相交，返回 null。

比如下圖中，兩個(gè)鏈表相交的節(jié)點(diǎn)是 3。

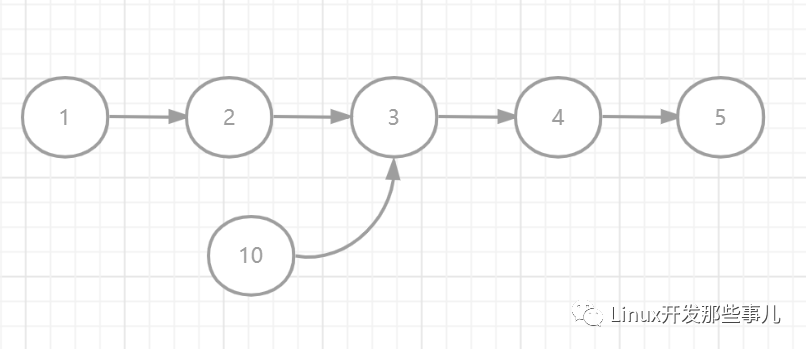
初看這個(gè)問題，最容易想到的方法是分別遍歷兩個(gè)鏈表，用一個(gè)集合記錄遍歷過程中的節(jié)點(diǎn)，如果存在相交的節(jié)點(diǎn)，肯定會多次訪問該節(jié)點(diǎn)，當(dāng)?shù)诙卧L問該節(jié)點(diǎn)的時(shí)候，集合中已經(jīng)存在該節(jié)點(diǎn)了，如果沒有相交，則集合中不會出現(xiàn)兩個(gè)相同的節(jié)點(diǎn)。

但利用集合臨時(shí)存儲遍歷過的節(jié)點(diǎn)的方法，空間復(fù)雜度是 O(N)，如何在 O(1) 的空間復(fù)雜度內(nèi)解決呢?

解決方法是利用兩個(gè)指針p1 和 p2，初始時(shí) p1 指向第一個(gè)鏈表的頭節(jié)點(diǎn)，p2指向第二個(gè)鏈表的頭節(jié)點(diǎn)，然后同時(shí)開始遍歷鏈表，p1 遍歷完鏈表之后，指向第二個(gè)鏈表的頭節(jié)點(diǎn)，p2 遍歷完鏈表之后，指向第一個(gè)鏈表的頭節(jié)點(diǎn)。

實(shí)際上相當(dāng)于兩個(gè)鏈表連在一起了，具體看下圖：

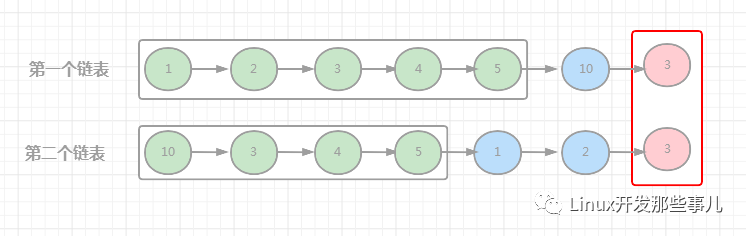
圖中綠色的節(jié)點(diǎn)是當(dāng)前鏈表的節(jié)點(diǎn)，藍(lán)色的節(jié)點(diǎn)是對方鏈表的節(jié)點(diǎn)，紅色的是遍歷過程中相遇的節(jié)點(diǎn)，也即兩個(gè)鏈表相交的節(jié)點(diǎn)，當(dāng)兩個(gè)鏈表沒有相交時(shí)，最后p1 和 p2 都指向了空節(jié)點(diǎn)，這也是我們想要的結(jié)果，大家可以自己模擬下這個(gè)過程。

因此，此題的關(guān)鍵是找到一種辦法，使得 p1 和 p2 能同時(shí)到達(dá)兩個(gè)鏈表相交的節(jié)點(diǎn)。

根據(jù)上述的方法，可以寫出實(shí)現(xiàn)代碼 :

// 單鏈表節(jié)點(diǎn)結(jié)構(gòu)
struct ListNode
{
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *pnext) : val(x), next(pnext) {}
};
//返回兩個(gè)鏈表相交的節(jié)點(diǎn)
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)
{
    if (nullptr == headA || nullptr == headB)
        return nullptr;
    ListNode *pa = headA;
    ListNode *pb = headB;
    while (pa != pb)
    {
        pa = (nullptr != pa) ? pa->next : headB;
        pb = (nullptr != pb) ? pb->next : headA;
    }
    return pa;
}

小結(jié)

本文講解了鏈表相關(guān)的一系列操作，有些方法比較有技巧性，一時(shí)不太容易想到，需要大家多去體會和練習(xí)，假以時(shí)日，我相信大家一定能掌握并熟練使用這些套路的