有人曾統計了某家互聯網公司的季度財報。結果顯示，該公司員工平均月薪是其他同行的3～4倍。消息一出，立即引起人們熱議。雖然后來這家公司出來辟謠，表明公開的酬金成本包括員工培訓、福利開支、繳納稅金、商業保險、年終獎，但這并沒能讓大眾信服。人們關心的問題是：統計平均工資的方法是否合理？

如果把一個普通員工和世界首富的工資放在一塊取平均值，那么可以想象，普通人的工資幾乎可以忽略不計。在一個企業中，20%的人占據了80%的工資總額。高收入的人比例偏少，但對平均工資的影響很大。

平均工資僅僅是經濟領域的一個例子。生活中，我們會接觸到各式各樣的數據，它們以不同的形態展現。在處理一組數據時，平均值可以很好地代表這組數據的平均水平，但由于削峰填谷，它也勢必會損失一部分信息，只能反映總體特征的一個方面。

想要掌握數據的全貌，就要了解數據的屬性和性質。對于一組數據，我們首先要知道大部分數值落在哪里？也就是說，我們通常選擇數據的“中間位置”，即反映數據集中趨勢的統計量，來表示數據的中心。這里的度量方法有平均數、中位數、眾數等。

01 平均數

平均數也叫平均值、均值，是統計學中最基本、最常用的一種定義一組數據特征的指標，用來描述數據的平均水平。計算平均數可以把所有數據相加再除以數據個數，比如{1，2，3，4，5}的平均數就是3。

盡管平均數是描述數據集最有用的一個統計量，但是它并非總是度量數據中心的最佳方法。最主要問題是平均數對極端值（比如離群點）很敏感，會被少數很低或很高的數值明顯影響。為了抵消這種影響，可以使用截尾均值，即丟棄一部分高低極端值后計算均值。比如跳水比賽，就采用去掉最高分和最低分的截尾均值計分法。

02 中位數

中位數是將數據按大小順序排列后處在中間位置的數，描述數據的中等水平。如果有奇數個數，則中位數是中間值；如果是偶數個數，則中位數一般取兩個最中間值的平均值。它適用于對傾斜（非對稱）數據的度量。

03 眾數

眾數是集合中出現頻率最高的數值，描述數據的一般水平。眾數的個數不一定是唯一的。一組數據中，可能會存在多個眾數，也可能不存在眾數。眾數不僅適用于數值型的數據，對于非數值型的數據也同樣適用。例如，{蘋果，蘋果，蘋果，香蕉，梨，梨}這組數據中，沒有均值和中位數，但是存在眾數—蘋果。

04 眾數、中位數、均值的關系

如果一組數據的平均值、中位數、眾數是同一個數，則說明它的數據分布是對稱的。但這種情況不常見，更多情況下，數據是正傾斜或負傾斜，如圖2-1所示。

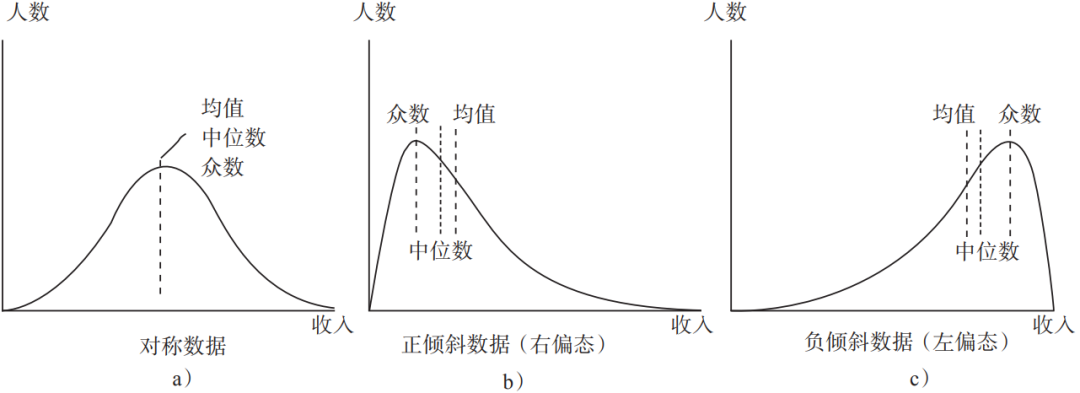▲圖2-1 眾數、中位數、均值的關系

收入數據就是典型的偏斜數據，大多數人是工薪階層或退休老人，只有少數幾個億萬富翁。收入數據如圖2-1中的正傾斜數據，大多數人的收入集中在左側，右側有一條長長的尾巴，表示少數人的收入。這種分布不適合用平均數來描述。因為平均數對極端數據非常敏感，一兩個億萬富翁，會拉高整個人群的收入水平線，使得收入均值比人們認知中的平均收入高出很多。

平均工資消除了大量低收入人群和少數巨額收入人群之間的差異。但如果換成眾數也不合適，因為低收入人群占了工資比例的大多數區間。統計工資時的合理選擇是統計中位數，它揭示了一半人和另一半人收入的分界線。

當然，并不是說中位數就是一個比平均數更好的統計量，只是它更適合工資統計。

引入統計量的意義就在于簡化。比如老師告訴你說，孩子考試的排名處于班級里面的后10%，你就應該意識到他的學習成績不太好，學習上要加把勁。在這個過程中，你不需要知道任何關于考試本身的內容，或孩子在考試中到底答對了多少題。一個排名數字，就能讓你了解孩子的學習水平。

不過也正是由于統計量的簡化，它不可避免地會丟失一些信息，其優點也是缺點。許多現象是無法只用一個數字來解釋的。如果單憑一個統計量描述對象具有局限性，我們就應該嘗試獲得更多的數據，以及更多的細節。

關于作者：徐晟，某商業銀行IT技術主管，畢業于上海交通大學，從事IT技術領域工作十余年，對科技發展、人工智能有自己獨到的見解，專注于智能運維（AIOps）、數據可視化、容量管理等方面工作。

本文摘編自《大話機器智能：一書看透AI的底層運行邏輯》，經出版方授權發布。（ISBN：9787111696193）