本文經AI新媒體量子位（公眾號ID:QbitAI）授權轉載，轉載請聯系出處。

探索游戲中的迷宮很有趣，然而玩多了就沒啥“新鮮感”了？

沒錯，如果游戲迷宮差別不大，時間一久就容易熟悉地圖，降低了探索的樂趣。

現在，一個“橫空出現”的概率編程語言 MarkovJunior 解決了這一問題：

利用馬爾科夫算法， 隨機生成批量迷宮 ，沒有一個是重復的，你永遠也不知道玩到的下一個迷宮長什么樣子：

不僅是 2D 迷宮，就連需要搭建好幾層地圖的 3D 迷宮，也能隨機生成：

這個項目一出，立刻上了 GitHub 熱榜， 不到一周就已經收獲 2.6k Star 。

有網友感嘆，用這個編程語言就能直接給 RPG 游戲或動作游戲生成建筑了。

Keras 的作者也對這個概率編程語言挺感興趣：

來看看它的原理究竟是什么、又是如何隨機生成各種迷宮的。

基于馬爾科夫算法構造

據作者介紹，這套概率編程語言借鑒了 馬爾科夫算法 （Markov algorithms）。

（MarkovJunior 這個名字，也是以提出馬爾科夫算法的數學家 Andrey Markov 命名）

具體來說，這套概率編程語言由一系列特定規則（Rewrite Rules，重寫規則）組成，是一個有序列表。

它在生成一個（迷宮）模型的過程中，會利用馬爾科夫算法實現“ 隨機生成 ”，再通過制定一系列特定規則，決定生成模型的類別，例如是迷宮、地形圖，還是電路圖等。

馬爾科夫鏈具有“無記憶”性質，即下一狀態的概率分布只能由當前狀態決定，在時間序列中它前面的事件均與之無關。

所以，這些特定規則究竟長啥樣？

例如，一個最簡單的規則，就是將“黑色”色塊重寫為“白色”色塊，直到最終填滿整個模型：

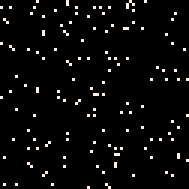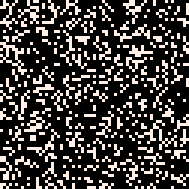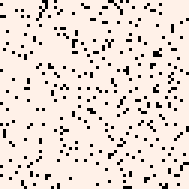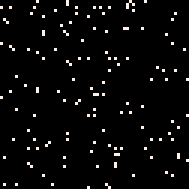
又例如，執行將“白-黑”色塊重寫為“白-白”色塊的規則，結合馬爾科夫算法，就能得到一個概率生成模型：

再例如，基于“推箱子游戲”的規則，

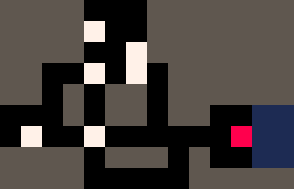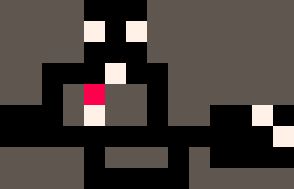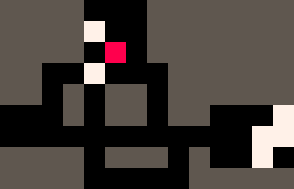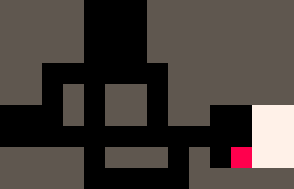
△ 推箱子游戲

就能用這批小紅點隨機將白色方塊“搬運”到指定地點：

像這樣的特定規則還有很多，都包含在 MarkovJunior 中。

那么，我們究竟要怎么利用這些規則，來生成一個隨機（迷宮、電路圖等）模型呢？

2D / 3D 迷宮、地形圖和電路圖都能畫

先以隨機生成一個 2D 迷宮為例：

從圖片中來看，這個迷宮算法會自動生成一個“起始點”紅點，在一塊黑色地圖中隨機探索并重寫路徑，最終填滿整個地圖，完成一個有始有終、也有分岔口的“迷宮”。

這樣的隨機迷宮，MarkovJunior 隨手就能做出一大把，只需要基于兩個規則：

第一個規則 ，將“紅-黑-黑”色塊隨機重寫為“綠-綠-紅”色塊。

第二個規則 ，在第一個規則被“卡住”，也就是沒有符合條件的可選項時，自動執行將“紅-綠-綠”色塊隨機重寫為“白-白-紅”色塊。

這樣一來，算法就能通過第一個規則生成隨機路徑，并通過第二個規則回溯還沒有經過的路徑、生成岔路口，最終遍歷整個黑色地圖，生成一套“2D 迷宮”。

還有更簡單的思路，將所有“白-黑-黑”替換成“白-A-白”，其中 A 是一個中間態，不作為起點，在迷宮生成完成后被替換為白色。

據作者表示，利用這個規則， 1 行代碼 就能隨機生成 2D 或 3D 迷宮。

▲ 3D 迷宮長這樣

基于這樣的思路，換套規則組合方法，還能生成隨機 地形圖 。

例如，試圖生成一塊河流地形圖，就只需要利用上面的生成模型方法，再添加一些其他的重寫規則，就能搞出一個隨機河流圖來：

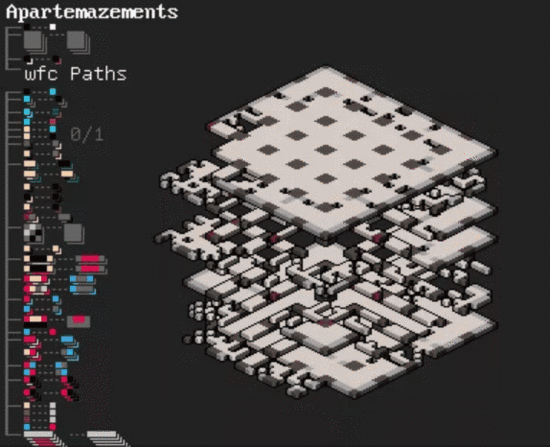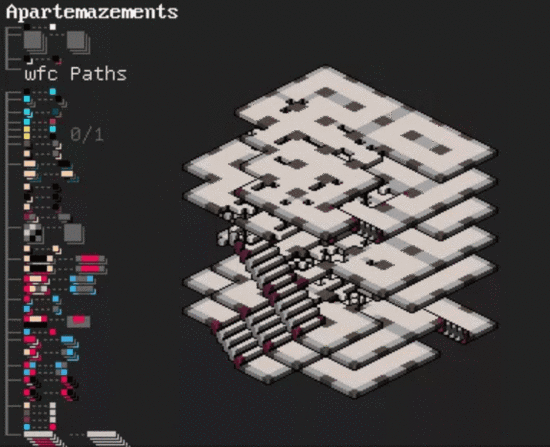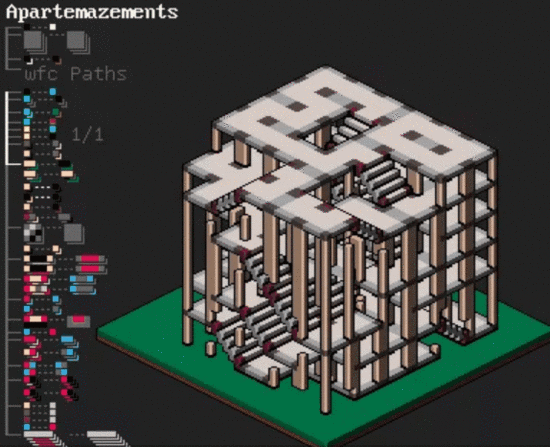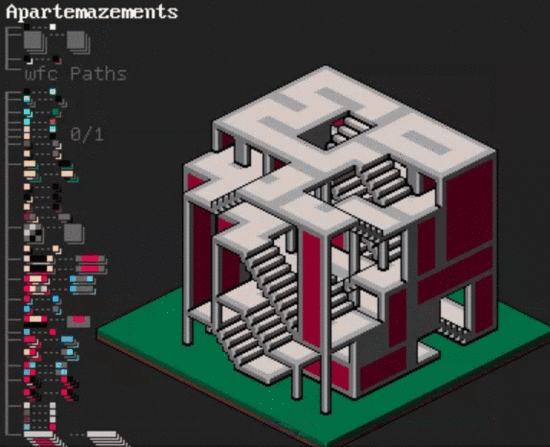
除了地形圖、簡單的 2D / 3D 迷宮，更復雜的 3D 建筑 也能搞定，只需要在兩層 2D“迷宮”之間的隨機位置生成一批“樓梯”：

嗯，連 電路圖 都能畫……

據作者介紹，只要靈活運用這些規則，就能用 MarkovJunior 隨機生成各種各樣的建筑和圖畫。

可以說是非常好用了。

還是著名 WFC 算法的作者

這個概率編程語言的作者 Maxim Gumin，是一名獨立游戲開發者。

他搞過最有名的項目，應該是一套叫做“ 波函數坍縮算法 ”（WaveFunctionCollapse，WFC）的東西，目前在 GitHub 上已經有 18.7k Stars 。

這套 WFC 算法是他受量子力學中“波函數坍縮”概念的啟發自創出來的，目前已經被應用到一些游戲中，如《城鎮疊疊樂》（Townscaper）等。

Maxim Gumin 并未透露更多自己的信息，但我們能在他的主頁上看到，這位老哥自稱“概率模型之王，程序化生成の彌賽亞，馴服馬爾科夫鏈的人……”（手動狗頭）

從 GitHub 來看，這些年他一直專注于將各種數學算法應用于程序化生成中，做出各種有意思的模型。

說不定你玩過的游戲中，有一些已經用過他開發的算法了。

項目地址：

https://github.com/mxgmn/MarkovJunior