譯者 | 朱先忠?

審校 | 孫淑娟?

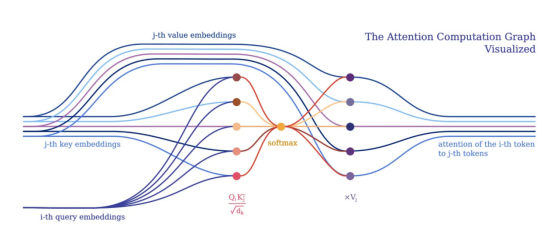
從令牌角度的注意力計算圖可視化（注意令牌間的關系）?

在過去幾年中，我們看到了不少基于Transformer的模型的興起（引文1），并在許多領域得到成功的應用，如自然語言處理或計算機視覺等。在本文中，我們將探索一種簡潔、可解釋和可擴展的方式，將深度學習模型（特別是Transformer）表達為混合架構，即通過將深度學習與符號人工智能相結合。為此，我們將使用一個名為PyNeuraLogic的基于Python語言的神經符號框架中實現模型設計。?

【注意】本文作者也是??PyNeuraLogic框架??的設計者之一。

“如果沒有混合架構、豐富的先驗知識和復雜的推理技術這三大要素，我們就無法以充分、自動化的方式構建豐富的認知模型。”（引文2）?

-加里·馬庫斯（新硅谷機器人創業公司Robust.AI首席執行官兼創始人）?

將符號表示與深度學習相結合，填補了當前深度學習模型中的空白，例如開箱即用的可解釋性或缺少推理技術等。也許，提高參數的數量并不是實現這些理想結果的最佳方法，就像增加相機百萬像素的數量不一定會產生更好的照片一樣。?

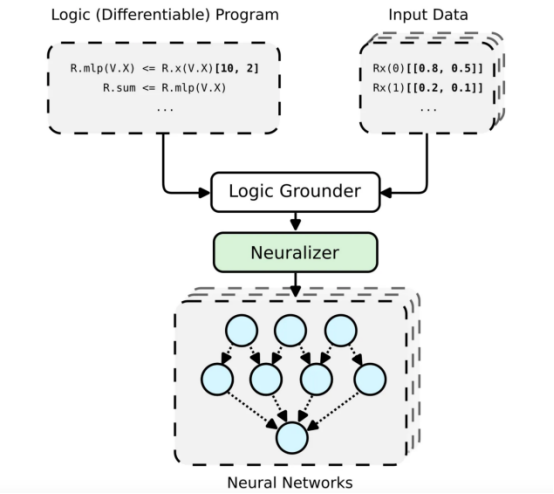
PyNeuraLogic框架工作流總體架構?

神經符號概念的高級可視化提升關系神經網絡（LRNN，見引文3），這可以借助（Py）NeuraLogic實現。這里我們展示了一個簡單的模板（邏輯程序）——通過一個線性層后面跟著一個求和聚合。對于每個（輸入）樣本，構建一個獨特的神經網絡。?

PyNeuraLogic框架是基于特別設計的邏輯編程（邏輯程序中包含可微參數）實現的。該框架非常適合于較小的結構化數據（如分子）和復雜模型（如Transformers和圖形神經網絡）。但是，另一方面需要注意的是，PyNeuraLogic不是非關系型和大張量數據的最佳選擇。?

框架的關鍵組成部分是一個可微邏輯程序，我們稱之為模板。模板由以抽象方式定義神經網絡結構的邏輯規則組成，我們可以將模板視為模型架構的藍圖。然后，將模板應用于每個輸入數據實例以產生（通過接地和神經化）輸入樣本特有的神經網絡。這個過程與其他具有預定義架構的框架完全不同，預定義架構無法根據不同的輸入樣本進行調整。為了更詳細地介紹該框架，您可以參考另一篇關于從圖形神經網絡的角度關注??PyNeuralogic的文章??。

符號式Transformer?

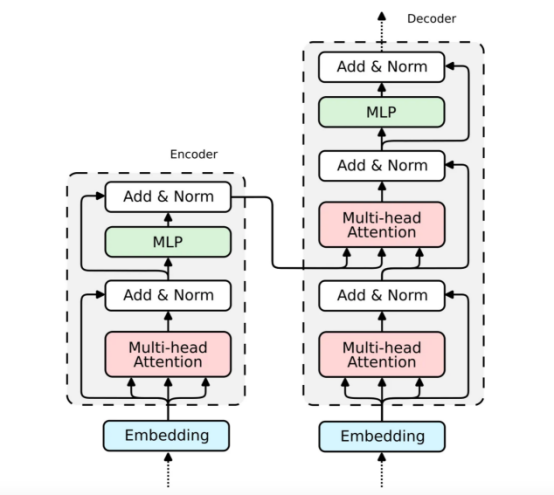
經典Transformer模型示意圖?

Transformer架構由兩個塊組成——編碼器（左）和解碼器（右）。兩個塊共享相似之處——解碼器是一個擴展編碼器。因此，在本文中我們將只關注編碼器的解析，因為解碼器的實現是類似的。?

我們通常傾向于將深度學習模型實現為對批量輸入到一個大張量中的輸入令牌的張量操作。這是有意義的，因為深度學習框架和硬件（例如GPU）通常被優化為處理更大的張量，而不是不同形狀和大小的多個張量。Transformers也不例外，通常將單個令牌向量表示批量化為一個大矩陣，并將模型表示為這些矩陣上的運算。然而，這樣的實現隱藏了各個輸入令牌之間的相互關系，正如Transformer的注意力機制所展示的那樣。?

注意力機制?

注意力機制是所有Transformer模型的核心。具體來說，它的經典版本利用了所謂的多頭縮放點積注意力。為了清晰起見，我們不妨借助于一個頭來將縮放的點積注意力分解成一個簡單的邏輯程序。?

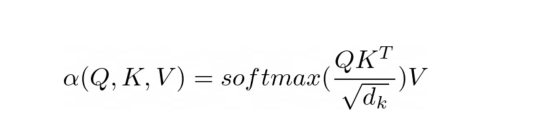
縮放的點積注意力方程?

注意力的目的是決定網絡應該關注輸入的哪些部分。注意力是通過計算值V的加權和來實現的，其中權重表示輸入鍵K和查詢Q的兼容性。在該特定版本中，通過查詢Q和鍵K的點積的softmax函數除以輸入特征向量維度d_k的平方根來計算權重。?

(R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])],?
(R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product]?

在PyNeuraLogic中，我們可以通過上述邏輯規則充分捕捉注意力機制。第一個規則表示權重的計算，它計算維度的平方根與轉置的第j個關鍵向量和第i個查詢向量的乘積。然后我們用softmax聚合給定i和所有可能j的所有結果。?

然后，第二條規則計算該權重向量與對應的第j個值向量之間的乘積，并對每個相應的第i個令牌的不同j的結果求和。?

注意力掩碼?

在訓練和評估期間，我們通常會限制輸入令牌可以注意的內容。例如，我們希望限制令牌向前看并注意即將出現的單詞。如PyTorch這樣的流行框架是通過掩碼技術實現這一點的，即通過將縮放的點積結果的元素子集設置為非常低的負數。這些數字強制softmax函數將零分配為相應令牌對的權重。?

(R.weights(V.I, V.J) <= (?
 R.d_k, R.k(V.J).T, R.q(V.I), R.special.leq(V.J, V.I)?
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],?

通過我們的符號表示，我們可以通過簡單地添加一個單體關系作為約束來實現這一點。在計算權重時，我們將j索引限制為小于或等于i索引。與掩碼方案相反，我們只計算所需的縮放點積。?

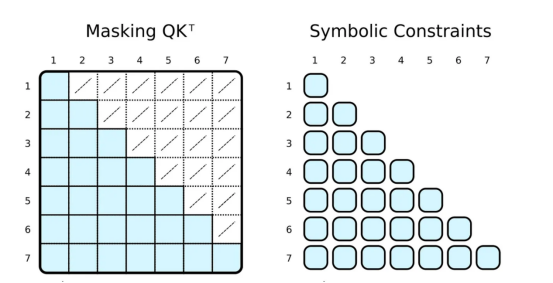
正則張量表示與符號表示中注意力的可視化?

常規的深度學習框架通過掩碼（左側）限制注意力。首先，計算整個QK^T矩陣，然后通過覆蓋低值（白色交叉單元格）來屏蔽值，以模擬只注意相關的令牌（藍色單元格）。在PyNeuraLogic中，我們通過應用符號約束（右側）只計算所需的標量值，因此沒有多余的計算。這一優勢在以下注意力版本中更為顯著。?

更優秀的注意力聚合?

當然，符號式的“掩碼”可以是完全任意的。我們大多數人都聽說過基于稀疏Transformer的GPT-3（或其應用程序，如ChatGPT，【引文4】）。稀疏Transformer的注意力（跨步版本）可分為兩種類型的注意力頭部：?

• 只關注前面的n個令牌（0≤i?j≤n）?
• 僅關注每n-th個前面的令牌（（i?j）%n=0）?

兩種類型的頭部的實現同樣只需要微小的修改（例如，對于n＝5）。?

(R.weights(V.I, V.J) <= (?
 R.d_k, R.k(V.J).T, R.q(V.I),?
 R.special.leq(V.D, 5), R.special.sub(V.I, V.J, V.D),?
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],?

(R.weights(V.I, V.J) <= (?
 R.d_k, R.k(V.J).T, R.q(V.I),?
 R.special.mod(V.D, 5, 0), R.special.sub(V.I, V.J, V.D),?
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],?

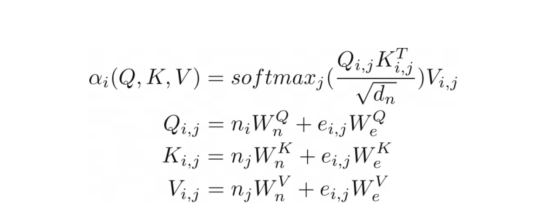
關系注意力方程?

其實，我們可以更進一步將注意力推廣到類似于圖的（關系）輸入，就像在關系注意力中一樣。這種類型的注意力作用于圖，其中節點只關注其鄰節點（由邊連接的節點）。然后，查詢Q、鍵K和值V是與節點向量嵌入相加的邊緣嵌入。?

(R.weights(V.I, V.J) <= (R.d_k, R.k(V.I, V.J).T, R.q(V.I, V.J))) | [F.product, F.softmax_agg(agg_terms=[V.J])],?
(R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.I, V.J)) | [F.product],?

R.q(V.I, V.J) <= (R.n(V.I)[W_qn], R.e(V.I, V.J)[W_qe]),?
R.k(V.I, V.J) <= (R.n(V.J)[W_kn], R.e(V.I, V.J)[W_ke]),?
R.v(V.I, V.J) <= (R.n(V.J)[W_vn], R.e(V.I, V.J)[W_ve]),?

在我們的示例中，這種注意力與之前顯示的縮放點積注意力幾乎相同。唯一的區別是添加了額外的術語來捕捉邊緣。將圖形作為注意力機制的輸入似乎很自然，考慮到Transformer是一種??圖形神經網絡??，作用于完全連接的圖形（當不應用掩碼時），這并不完全令人驚訝。在傳統的張量表示中，這不是那么明顯。

Transformer編碼器?

現在，我們已經展示注意力機制的實現。其實，構建整個Transformer編碼器塊所缺少的部分也是比較直觀的。?

嵌入?

我們已經在關系注意（Relational Attention）中看到了如何實現嵌入。對于傳統的Transformer，嵌入都是非常相似的。我們只需將輸入向量投影為三個嵌入向量——鍵、查詢和值。?

R.q(V.I) <= R.input(V.I)[W_q],?
R.k(V.I) <= R.input(V.I)[W_k],?
R.v(V.I) <= R.input(V.I)[W_v],?

跳過連接、標準化和前饋網絡?

查詢嵌入通過跳過連接與注意力輸出相加。然后將得到的向量歸一化并傳遞到多層感知器（MLP）中。?

(R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm],?

對于MLP，我們將實現具有兩個隱藏層的完全連接的神經網絡，這可以優雅地表示為一個邏輯規則。?

(R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu],?

最后一個帶有規范化的跳過連接與前一個相同。?

(R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],?

組裝到一起?

至此，我們已經構建了Transformer編碼器所需的所有部件。解碼器使用相同的組件；因此，它的實現是類似的。現在，讓我們將上面所有的代碼塊組合成一個可微的邏輯程序中。該程序可以嵌入到Python腳本內，并通過使用PyNeuraLogic被編譯成神經網絡。?

R.q(V.I) <= R.input(V.I)[W_q],?
R.k(V.I) <= R.input(V.I)[W_k],?
R.v(V.I) <= R.input(V.I)[W_v],?

R.d_k[1 / math.sqrt(embed_dim)],?
(R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])],?
(R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product],?

(R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm],?
(R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu],?
(R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],?

結論?

在本文中，我們分析了Transformer架構，并演示了它在一個稱為??PyNeuraLogic???的神經符號框架中的實現。通過這種方法，我們能夠在只需對代碼進行微小的更改的情況下實現各種類型的Transformer，從而向廣大讀者展示了如何快速地轉向和開發新的Transformer架構。此外，文章還指出了各種版本的Transformer以及帶有圖形神經網絡（GNN）的Transformer的明顯相似之處。

參考文獻?

[1]: Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A., Kaiser, L., & Polosukhin, I.. (2017). Attention Is All You Need.?

[2]: Marcus, G.. (2020). The Next Decade in AI: Four Steps Towards Robust Artificial Intelligence.?

[3]: Gustav ?ourek, Filip ?elezny, & Ond?ej Ku?elka (2021). Beyond graph neural networks with lifted relational neural networks. Machine Learning, 110(7), 1695–1738.?

[4]: Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J., Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G., Askell, A., Agarwal, S., Herbert-Voss, A., Krueger, G., Henighan, T., Child, R., Ramesh, A., Ziegler, D., Wu, J., Winter, C., Hesse, C., Chen, M., Sigler, E., Litwin, M., Gray, S., Chess, B., Clark, J., Berner, C., McCandlish, S., Radford, A., Sutskever, I., & Amodei, D.. (2020). Language Models are Few-Shot Learners.?

[5]: Child, R., Gray, S., Radford, A., & Sutskever, I.. (2019). Generating Long Sequences with Sparse Transformers.?

1. : Diao, C., & Loynd, R.. (2022). Relational Attention: Generalizing Transformers for Graph-Structured Tasks.?

譯者介紹?

朱先忠，51CTO社區編輯，51CTO專家博客、講師，濰坊一所高校計算機教師，自由編程界老兵一枚。?

原文標題：??Beyond Transformers with PyNeuraLogic??，作者：Luká? Zahradník