圖形編輯器開發:一些會用到的簡單幾何算法

大家好,我是前端西瓜哥。
開發圖形編輯器,你會經常要解決一些算法問題。本文盤點一些我開發圖形編輯器時常用到的簡單幾何算法。
矩形碰撞檢測
判斷兩個矩形是否發生碰撞(或者說相交),即兩個矩形有重合的區域。

常見使用場景:
使用選擇工具框選圖形(框選策略除了相交,還可以用相交或其他方案)。
遍歷圖形,通過判斷視口矩形和圖形包圍盒的矩形碰撞,剔除掉視口外的圖形渲染操作,提高性能。
export function isRectIntersect2(rect1: IBox2, rect2: IBox2) {
return (
rect1.minX <= rect2.maxX &&
rect1.maxX >= rect2.minX &&
rect1.minY <= rect2.maxY &&
rect1.maxY >= rect2.minY
);
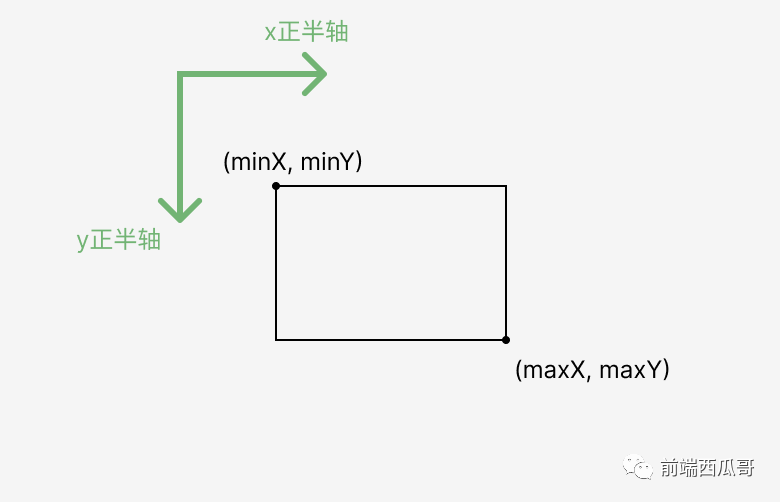
}關于 IBox2 為包圍盒的接口簽名:
interface IBox2 {
minX: number;
minY: number;
maxX: number;
maxY: number;
}
矩形包含檢測
該算法用于判斷矩形 1 是否包含矩形 2。

常見使用場景:
使用選擇工具框選圖形(這次用的是包含策略);
function isRectContain2(rect1: IBox2, rect2: IBox2) {
return (
rect1.minX <= rect2.minX &&
rect1.minY <= rect2.minY &&
rect1.maxX >= rect2.maxX &&
rect1.maxY >= rect2.maxY
);
}計算旋轉后坐標
對圖形旋轉,是一個非常基礎的功能。計算旋轉后的點是很常見的需求。
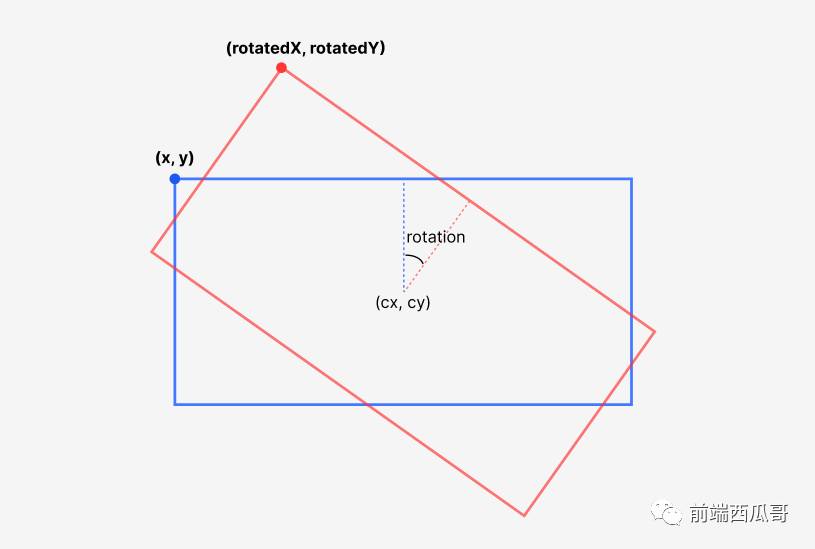
常見使用場景:
- 計算包圍盒旋轉后的坐標,繪制縮放控制點。
- 計算光標位置是否落在一個旋轉的矩形上,因為旋轉的矩形并不是一個正交的矩形,計算出來后判斷有點復雜。所以通常我們會將光標給予矩形的中點反過來旋轉一下,然后判斷點是否在矩形中。
用到三角函數算法。
const transformRotate = (
x: number,
y: number,
radian: number,
cx: number,
cy: number,
) => {
if (!radian) {
return { x, y };
}
const cos = Math.cos(radian);
const sin = Math.sin(radian);
return {
x: (x - cx) * cos - (y - cy) * sin + cx,
y: (x - cx) * sin + (y - cy) * cos + cy,
};
}點是否在矩形中

常見使用場景:
用于實現圖形拾取,判斷矩形圖形或包圍盒是否在光標位置上。
function isPointInRect(point: IPoint, rect: IRect) {
return (
point.x >= rect.x &&
point.y >= rect.y &&
point.x <= rect.x + rect.width &&
point.y <= rect.y + rect.height
);
}多個矩形組成的大矩形
選中多個矩形時,要計算它們組成的大矩形,然后繪制出大選中框。
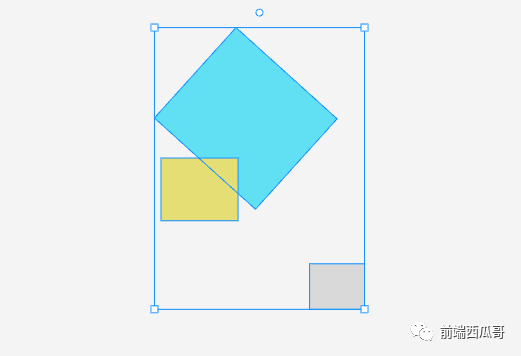
function getRectsBBox(...rects: IRect[]): IBox {
if (rects.length === 0) {
throw new Error('the count of rect can not be 0');
}
const minX = Math.min(...rects.map((rect) => rect.x));
const minY = Math.min(...rects.map((rect) => rect.y));
const maxX = Math.max(...rects.map((rect) => rect.x + rect.width));
const maxY = Math.max(...rects.map((rect) => rect.y + rect.height));
return {
x: minX,
y: minY,
width: maxX - minX,
height: maxY - minY,
};
}這里用的是另一種包圍盒子的表達,所以多了一層轉換。
interface IRect = {
x: number;
y: number;
width: number;
height: number;
}
type IBox = IRect計算向量夾角
通過旋轉控制點旋轉圖形時,需要通過向量的點積公式來計算移動的夾角,去更新圖形的旋轉角度。
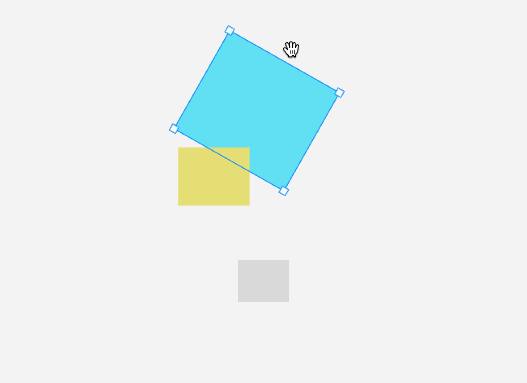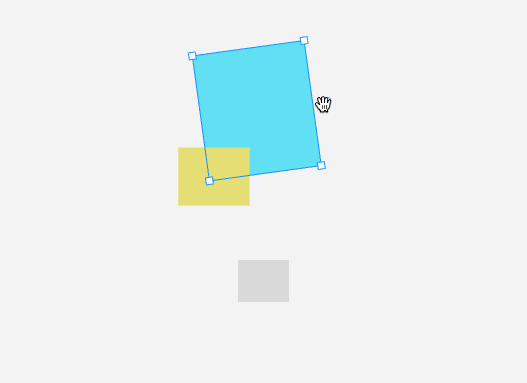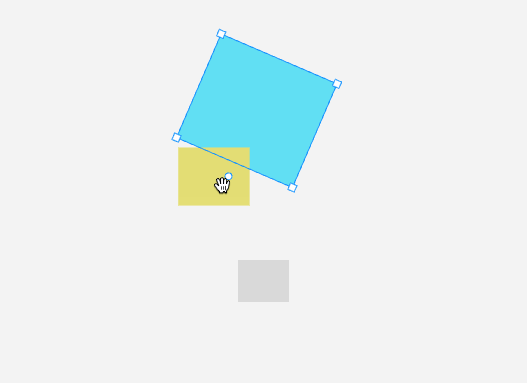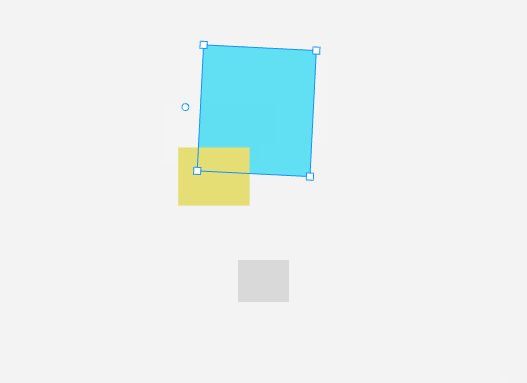
計算 [x - cx, y - cy] 和 [0, -1] 兩個向量夾角的算法實現:
/**
* 求向量到右側軸(x正半軸)的夾角
* 范圍在 [0, Math.PI * 2)
*/
export function calcVectorRadian(cx: number, cy: number, x: number, y: number) {
const a = [x - cx, y - cy];
const b = [0, -1];
const dotProduct = a[0] * b[0] + a[1] * b[1];
const d =
Math.sqrt(a[0] * a[0] + a[1] * a[1]) * Math.sqrt(b[0] * b[0] + b[1] * b[1]);
let radian = Math.acos(dotProduct / d);
if (x < cx) {
radian = Math.PI * 2 - radian;
}
return radian;
}結尾
做圖形編輯器,經常要和幾何算法打交道,各種相交判斷、居中計算、光標縮放、找最近的參照線等等。
這對算法能力有一定要求的,建議多去刷刷 leetcode。此外就是多畫圖分析。
在開發中,我們還要自己去分析需求,結合圖形編輯器的具體實現,抽離出算法問題,并配合合適的數據結構,去解題。解法可能一次不是最優解, 但我們可以慢慢迭代,慢慢優化的。
雖然有點耗腦細胞,但最后把難題解決,還是非常有成就感。










































