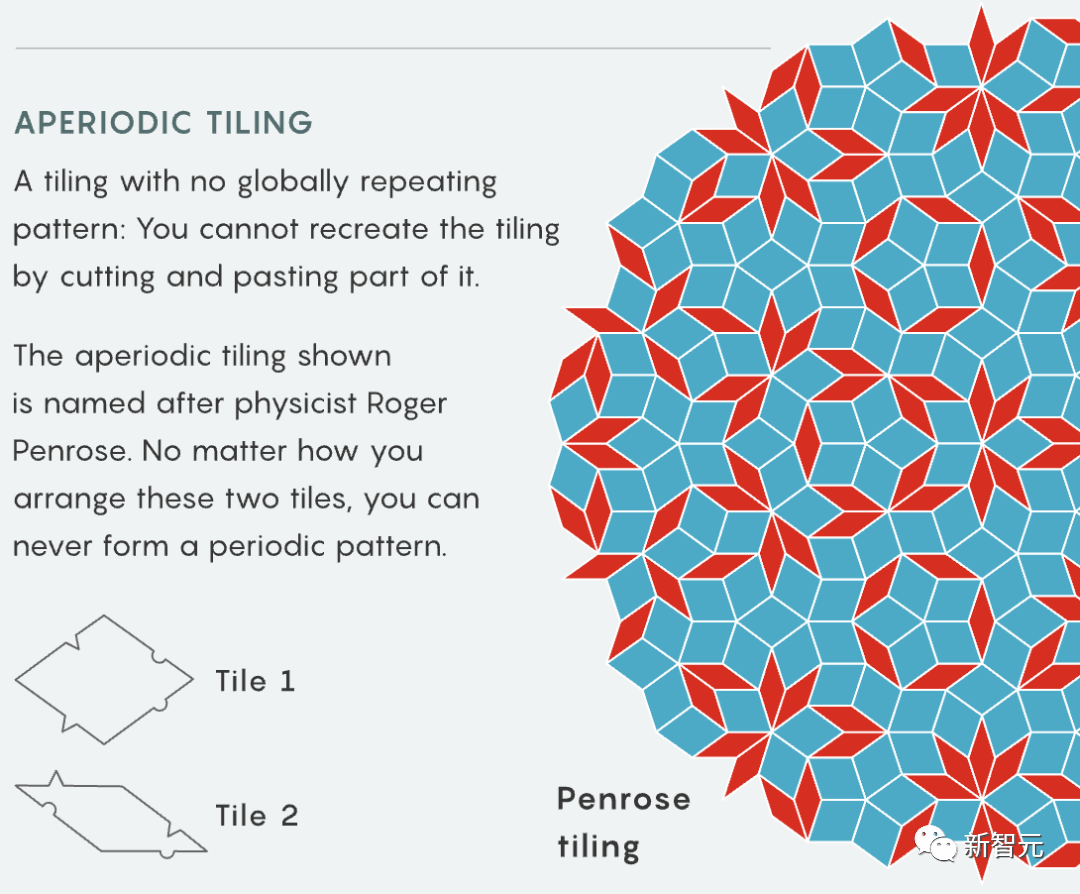
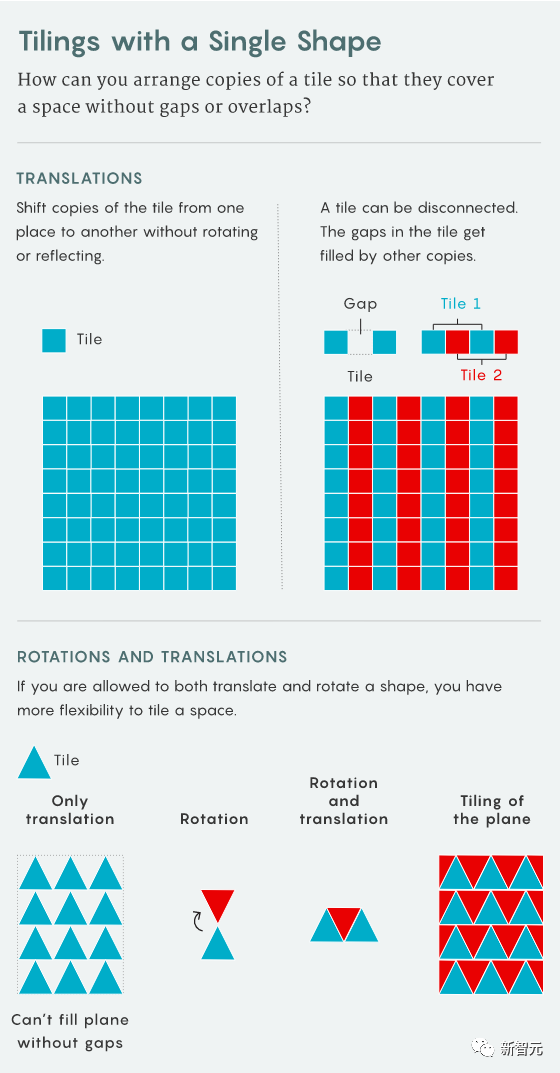
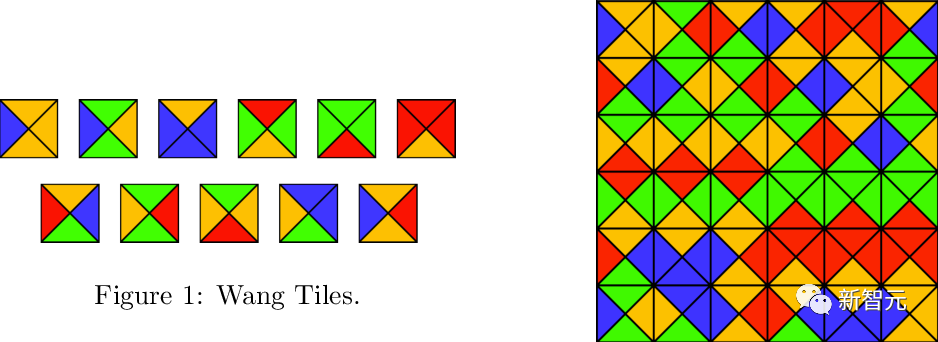
陶哲軒再逼近60年幾何學難題!周期性密鋪問題又獲新突破
陶哲軒一直在研究的周期性密鋪問題,又有新突破了。
9月18日,陶哲軒和Rachel Greenfeld將預印本論文《平移單密鋪的不可判定性 (Undecidability of translational monotilings)》上傳到了arXiv。

論文地址:https://arxiv.org/abs/2309.09504
這篇論文的主要結論是,如果網格的維數是無界的,那么確定網格的有限子集是否可以平鋪該網格的周期子集的問題,就是不可判定的。
要知道,此問題在維度1和維度2中是可判定的。
陶哲軒表示,有點奇怪的是,文中所證明的大多數組件都跟流行的游戲類似——
多米諾骨牌的密鋪類似物,數獨,電腦游戲「俄羅斯方塊」,甚至連兒童游戲「Fizz buzz」都出現了。
為什么研究一個數學問題,會涉及到這么多游戲呢?陶哲軒也無法解釋。

平移單密鋪的不可判定性
這次的論文,是兩人上一篇論文的續集。鏈接 周期性密鋪問題
在上篇論文中,他們構建了一個高維網格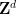 的平移單密鋪
的平移單密鋪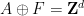
(因此單密鋪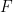 是一個有限集合 ),它是非周期性的(沒有辦法將這個密鋪「修復」成周期性密鋪
是一個有限集合 ),它是非周期性的(沒有辦法將這個密鋪「修復」成周期性密鋪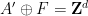 ,其中
,其中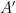 現在相對于有限索引子群
現在相對于有限索引子群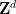 是周期性的)。
是周期性的)。

這就反駁了Stein、Grunbaum-Shephard和Lagarias-Wang的周期性密鋪猜想,他們斷言這種非周期性密鋪單體不存在。
(「帽子單密鋪」是一種最近發現的非周期等距單密鋪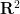 ,在這種單密鋪中,可以允許使用旋轉、反射以及平移,或者更新的「幽靈單片」。上述單片與帽子單密鋪相似,除了不需要反射)。
,在這種單密鋪中,可以允許使用旋轉、反射以及平移,或者更新的「幽靈單片」。上述單片與帽子單密鋪相似,除了不需要反射)。
激發陶哲軒和Rachel Greenfeld這個猜想的原因之一,是數學家Hao Wang的觀察。

他發現,如果周期密鋪猜想為真,那么平移密鋪問題在算法上是可判定的——
有一個圖靈機,對于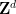 ,當給定一個維度
,當給定一個維度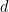 和一個有限子集
和一個有限子集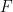 時,可以在有限的時間內確定
時,可以在有限的時間內確定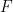 是否可以密鋪
是否可以密鋪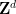 。
。
這是因為如果存在周期性密鋪,就可以通過計算機搜索找到它。
如果根本不存在密鋪,那么通過緊致性定理可知,存在一些有限的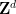 子集,這些子集不能被
子集,這些子集不能被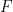 不相交的平移所覆蓋,這也可以通過計算機搜索來發現。
不相交的平移所覆蓋,這也可以通過計算機搜索來發現。
周期性密鋪猜想斷言這是僅有的兩種可能的情況,從而給出了可判定性。

另一方面,Wang的論點是不可逆的:周期性密鋪猜想的失敗,并不自動意味著平移單密鋪問題的不可判定性,因為它不排除存在一些其他算法來確定密鋪,這種密鋪可以不依賴于周期性密鋪的存在。
(例如,即使有新發現的帽子和幽靈密鋪,對于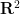 中有理系數的多邊形的等距單密鋪問題是否是可判定的,仍然是一個懸而未決的問題,無論它有沒有反射。
中有理系數的多邊形的等距單密鋪問題是否是可判定的,仍然是一個懸而未決的問題,無論它有沒有反射。
本文的主要結果解決了這個問題(有一個警告):

定理1
不存在任何算法,對于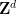 ,給定一個維度
,給定一個維度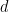 ,一個周期性子集
,一個周期性子集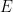 ,和一個有限子集
,和一個有限子集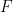 ,能在有限時間內確定是否存在一個平移密鋪
,能在有限時間內確定是否存在一個平移密鋪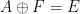 。
。
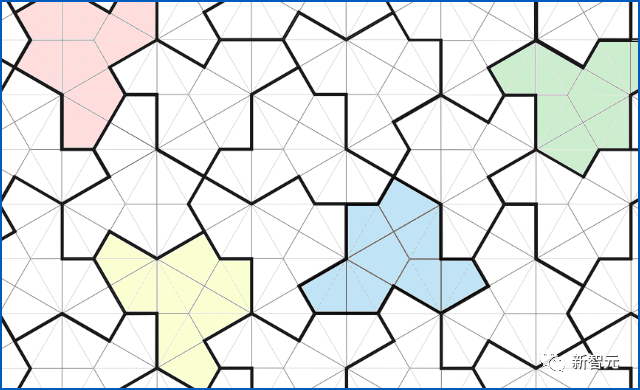
需要注意的是,必須使用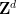 的周期性子集
的周期性子集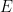 ,而不是全部的
,而不是全部的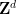 ;這在很大程度上是由于這種方法的技術限制,并且很可能通過額外的努力和創造力來消除。
;這在很大程度上是由于這種方法的技術限制,并且很可能通過額外的努力和創造力來消除。
另外,陶哲軒和Rachel Greenfeld還注意到,當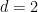 ,周期性密鋪猜想是由Bhattacharya建立的,因此在
,周期性密鋪猜想是由Bhattacharya建立的,因此在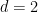 這種情況下問題可判定。
這種情況下問題可判定。
對于任何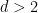 的固定值,密鋪問題是否可判定仍然是開放的(注意,在上面的結果中,維度
的固定值,密鋪問題是否可判定仍然是開放的(注意,在上面的結果中,維度 不是固定的,而是輸入的一部分)。
不是固定的,而是輸入的一部分)。
由于算法不可判定性和邏輯不可判定性(也稱為邏輯獨立性)之間存在眾所周知的聯系,此定理還暗示了存在一個(原則上明確可描述的)維度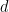 、
、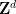 的周期性子集
的周期性子集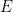 ,
,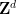 的有限子集
的有限子集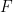 ,使得
,使得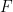 能通過平移密鋪
能通過平移密鋪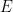 不能在ZFC集合論中被證實或證偽(當然假設這個理論是一致的)。
不能在ZFC集合論中被證實或證偽(當然假設這個理論是一致的)。
作為這種方法的結果,我們也可以在這里用「幾乎二維」群 來代替
來代替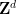 ,其中
,其中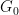 是一個有限阿貝爾群(現在成為輸入的一部分,代替維度
是一個有限阿貝爾群(現在成為輸入的一部分,代替維度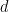 )。
)。
接下來,描述證明的一些主要思想。
證明某個問題不可判定的常用方法是,將已知不可判定的其他問題「編碼」到原始問題中,這樣,任何判定原始問題的算法也能判定嵌入的問題。
因此,我們將 Wang密鋪問題編碼為單密鋪問題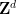 :
:

問題2(Wang密鋪問題)
給定一個有限的王氏密鋪集合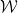 (單位正方形,每條邊都從有限調色板中指定了某種顏色),是否有可能用標準的格
(單位正方形,每條邊都從有限調色板中指定了某種顏色),是否有可能用標準的格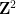 通過平移來密鋪平面,使得相鄰的密鋪在共同邊緣上具有相同的顏色?
通過平移來密鋪平面,使得相鄰的密鋪在共同邊緣上具有相同的顏色?
Berger曾給出一個著名的結果,即這個問題是不可判定的。

Berger, Robert,<The undecidability of the domino problem>
將這一問題嵌入高維平移單密鋪問題需要經過一些中間問題。
首先,我們可以很容易地將王氏密鋪問題嵌入到一個類似的問題中,我們稱之為多米諾骨牌問題:

問題 3(多米諾骨牌問題)
給定一個水平(或垂直)的多米諾骨牌的有限集合 或
或 ,它們是一對相鄰的單元正方形,每個單元正方形都用有限集合
,它們是一對相鄰的單元正方形,每個單元正方形都用有限集合 中的一個元素點來點綴,是否可以在標準格密鋪
中的一個元素點來點綴,是否可以在標準格密鋪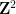 中為每個單元正方形分配一個點,使得這個密鋪中的每一對水平(或垂直)的方格都能用到來自
中為每個單元正方形分配一個點,使得這個密鋪中的每一對水平(或垂直)的方格都能用到來自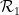 或
或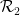 的多米諾骨牌?
的多米諾骨牌?

事實上,我們只需要將每個王氏密鋪作為一個單獨的「點」插入,并定義多米諾骨牌集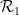 ,
,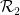 為水平或垂直相鄰、邊緣具有相同顏色的王氏密鋪對。
為水平或垂直相鄰、邊緣具有相同顏色的王氏密鋪對。
接下來,將多米諾骨牌問題嵌入到數獨問題中:

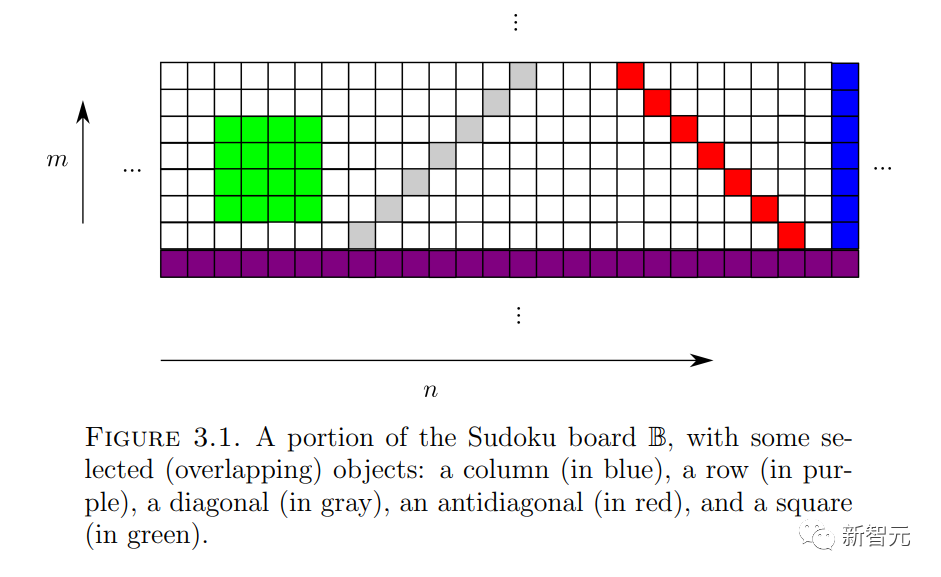
問題 4(數獨問題)
給定列寬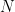 、數字集
、數字集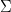 、函數
、函數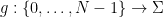 的集合
的集合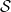 和「初始條件」
和「初始條件」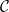 (在這里就不詳細介紹了),是否可以為「數獨棋盤」
(在這里就不詳細介紹了),是否可以為「數獨棋盤」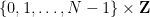 中的每個單元格
中的每個單元格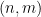 分配一個數字
分配一個數字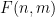 ,以便對于任何斜率
,以便對于任何斜率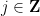 和截距
和截距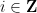 ,沿著
,沿著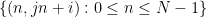 線的數字
線的數字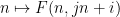 位于
位于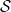 中(并且
中(并且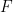 服從初始條件
服從初始條件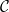 )?
)?
這篇論文最新穎的部分是證明了多米諾骨牌問題確實可以嵌入到數獨問題中。
將數獨問題嵌入到單密鋪問題中,源于之前論文中修改的方法。
這些論文也引入了數獨問題的版本,并創造了一種「密鋪語言」,可用于把各種問題(包括數獨問題)「編碼」為單密鋪問題。
要將多米諾骨牌問題編碼為數獨問題,我們需要獲取一個多米諾函數
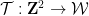 (遵守與某些多米諾骨牌集
(遵守與某些多米諾骨牌集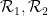 相關的多米諾骨牌約束),并使用它來構建數獨函數
相關的多米諾骨牌約束),并使用它來構建數獨函數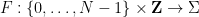 (遵守與多米諾骨牌集相關的一些數獨約束);反過來說,每個遵守數獨謎題規則的數獨函數,都必須以某種方式從多米諾函數中產生。
(遵守與多米諾骨牌集相關的一些數獨約束);反過來說,每個遵守數獨謎題規則的數獨函數,都必須以某種方式從多米諾函數中產生。
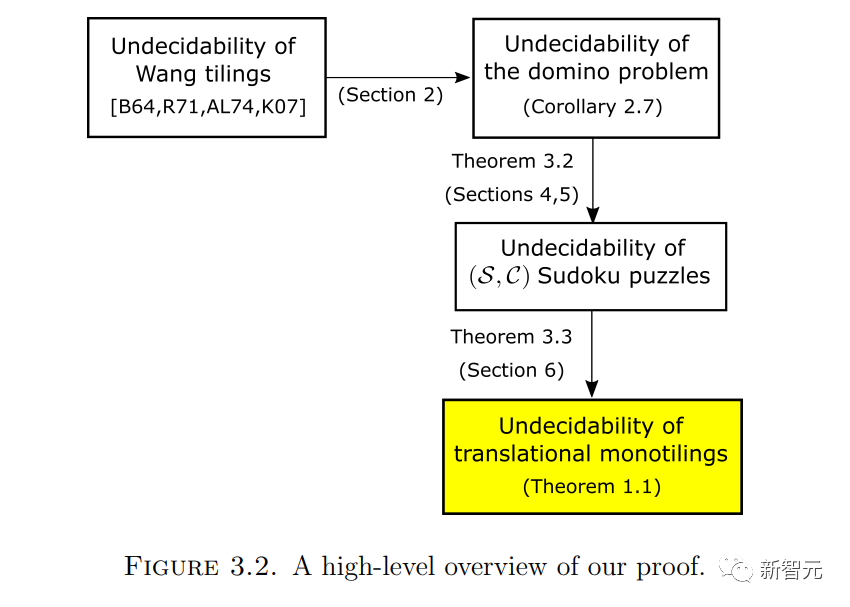
這種做法并不是很顯而易見,但是在Emmanuel Jeandel的幫助下,陶哲軒和Rachel Greenfeld改編了Aanderaa和Lewis的一些想法,某些層次結構被用來將一個問題編碼另一個問題。
在這里,我們解釋分層結構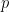 (由于多米諾骨牌問題的二維性,需要使用兩個不同的素數)。
(由于多米諾骨牌問題的二維性,需要使用兩個不同的素數)。
然后,通過公式 用
用 構建數獨函數
構建數獨函數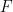 ,它將體現某種嵌入。
,它將體現某種嵌入。
其中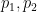 是兩個不同的大素數(例如,可以取
是兩個不同的大素數(例如,可以取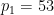 ,
,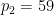 ),
),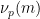 表示
表示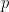 除以
除以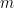 的次數,并且
的次數,并且
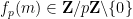 是
是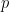 的
的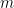 展開中的最后一個非零數字:
展開中的最后一個非零數字:
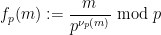
(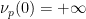 ,且
,且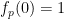 )。
)。
在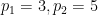 的情況下,(1) 的第一個分量如下所示:
的情況下,(1) 的第一個分量如下所示:
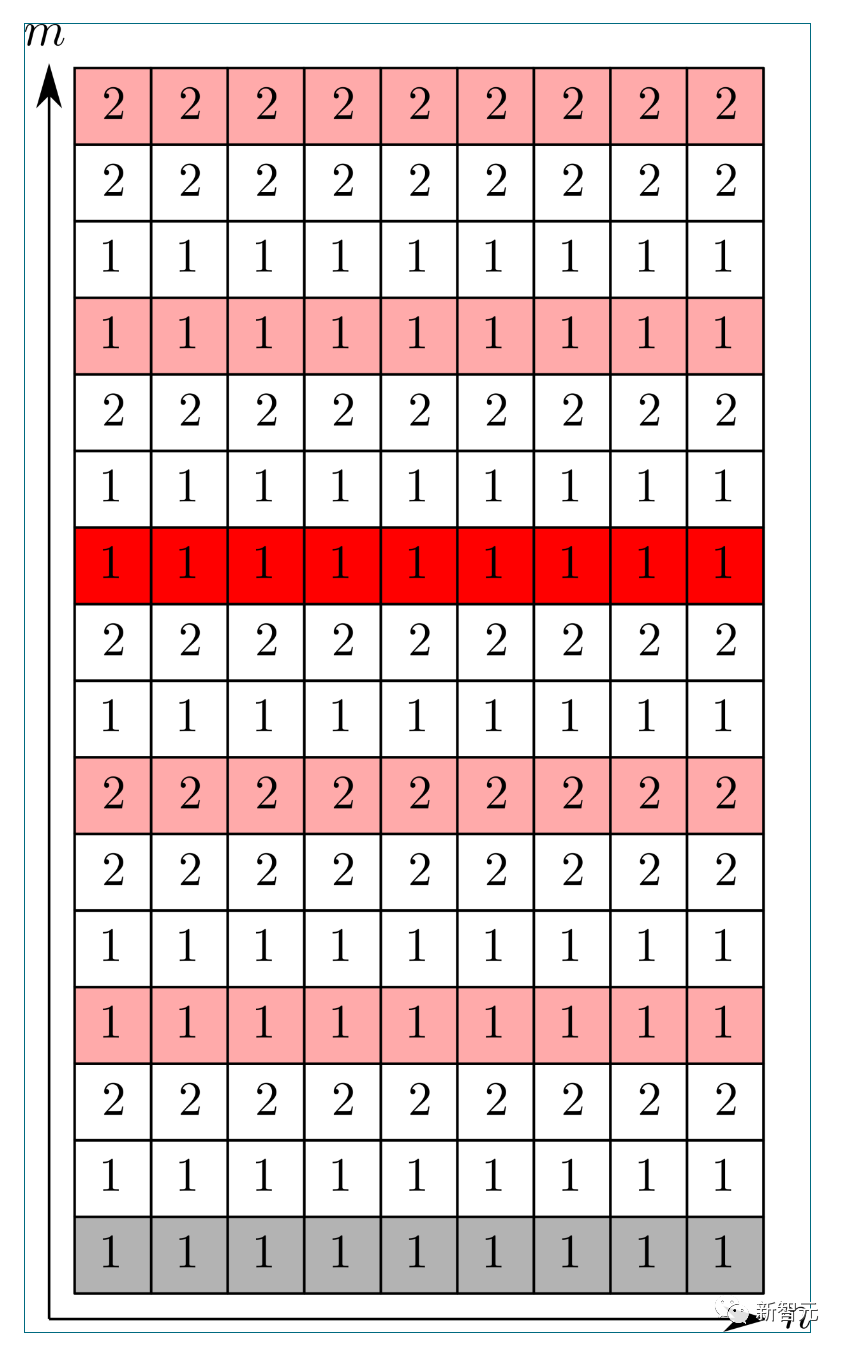
最終分量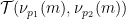 的典型實例如下所示:
的典型實例如下所示:
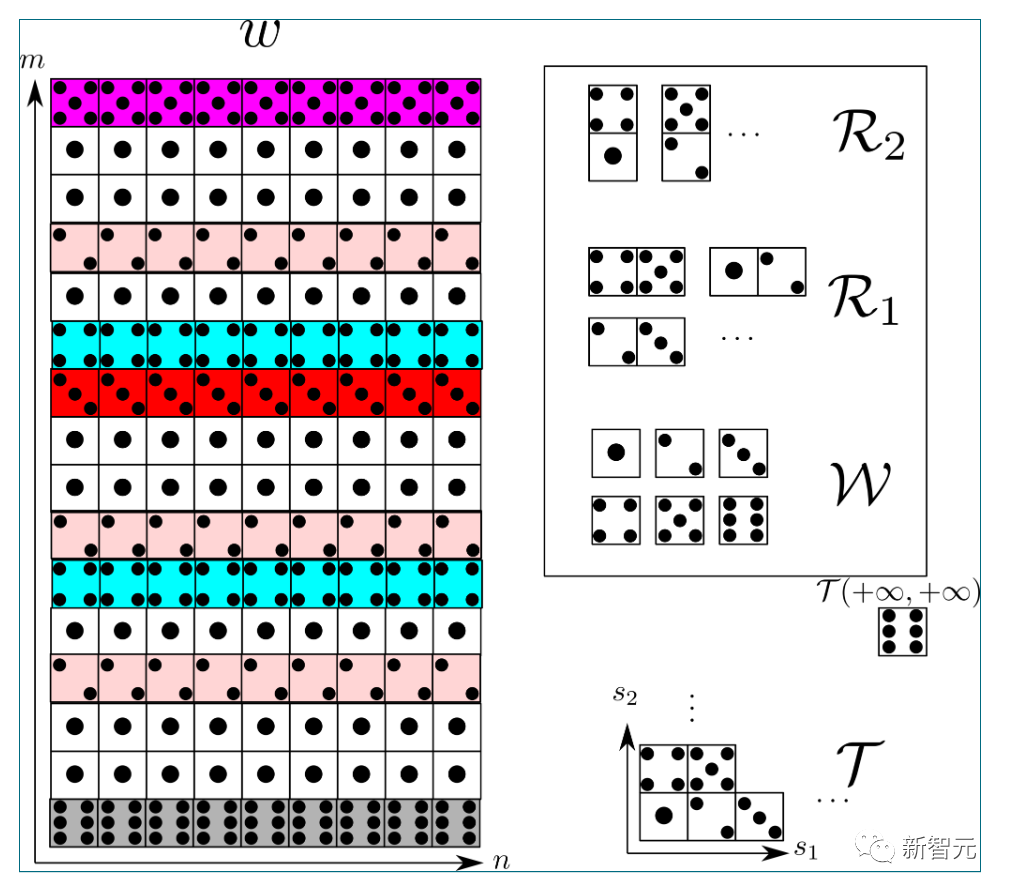
有趣的是,不知為何,這里的裝飾基本上遵循了兒童游戲「Fizz buzz」的規則。












































