幾行代碼穩定UNet ! 中山大學等提出ScaleLong擴散模型:從質疑Scaling到成為Scaling
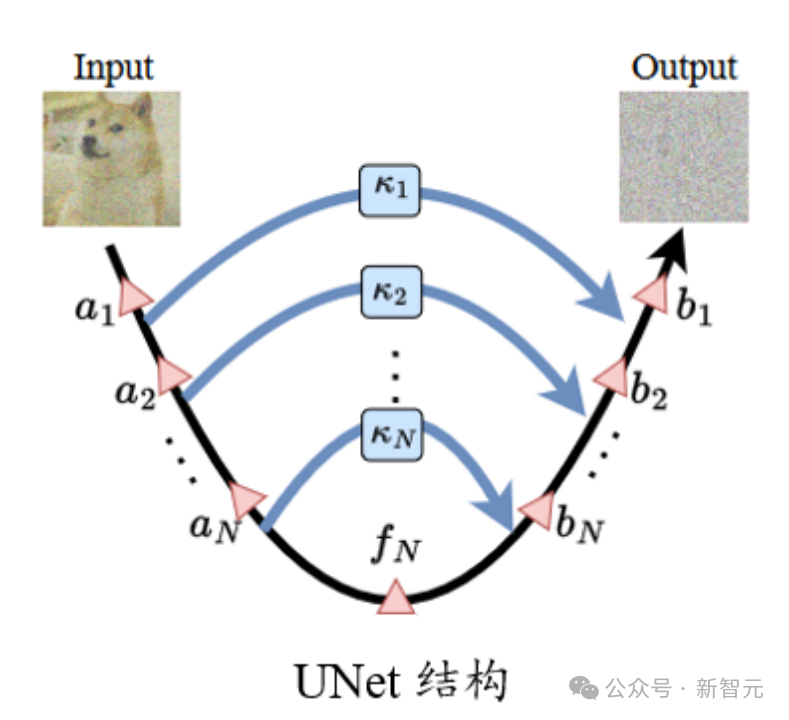
在標準的UNet結構中,long skip connection上的scaling系數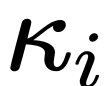 一般為1。
一般為1。
然而,在一些著名的擴散模型工作中,比如Imagen, Score-based generative model,以及SR3等等,它們都設置了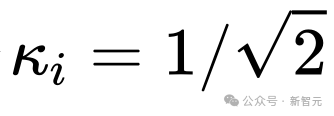 ,并發現這樣的設置可以有效加速擴散模型的訓練。
,并發現這樣的設置可以有效加速擴散模型的訓練。
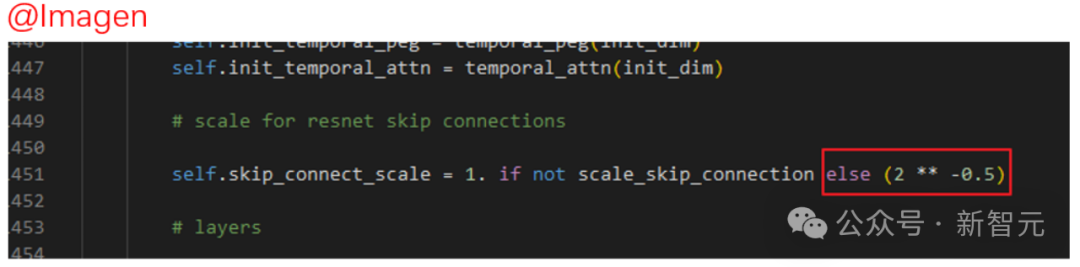
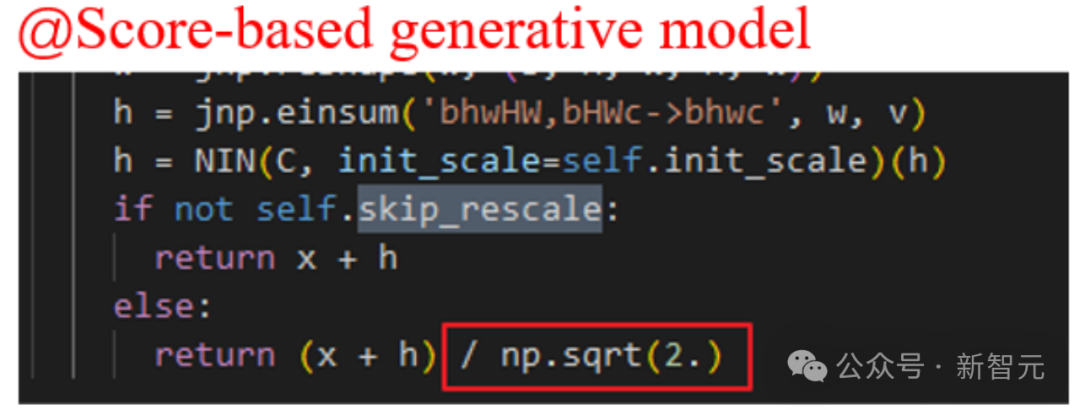
質疑Scaling然而,Imagen等模型對skip connection的Scaling操作在原論文中并沒有具體的分析,只是說這樣設置有助于加速擴散模型的訓練。
首先,這種經驗上的展示,讓我們并搞不清楚到底這種設置發揮了什么作用?
另外,我們也不清楚是否只能設置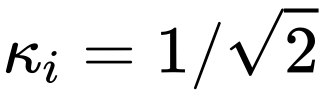 ,還是說可以使用其他的常數?
,還是說可以使用其他的常數?
不同位置的skip connection的「地位」一樣嗎,為什么使用一樣的常數?
對此,作者有非常多的問號……
 圖片
圖片
理解Scaling
一般來說,和ResNet以及Transformer結構相比,UNet在實際使用中「深度」并不深,不太容易出現其他「深」神經網絡結構常見的梯度消失等優化問題。
另外,由于UNet結構的特殊性,淺層的特征通過long skip connection與深層的位置相連接,從而進一步避免了梯度消失等問題。
那么反過來想,這樣的結構如果稍不注意,會不會導致梯度過猛、參數(特征)由于更新導致震蕩的問題?
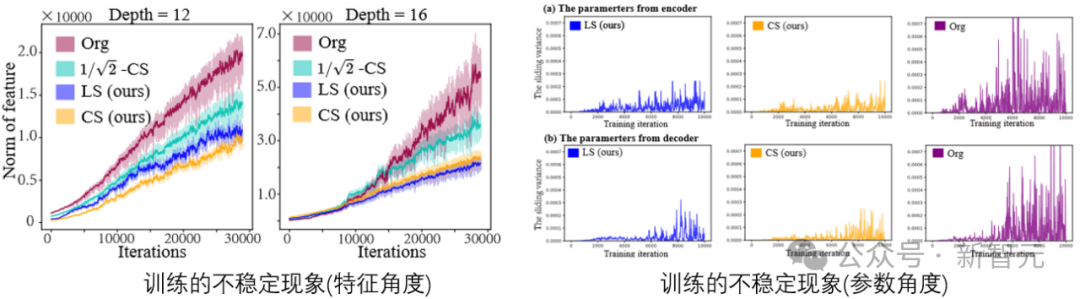 圖片
圖片
通過對擴散模型任務在訓練過程中特征和參數的可視化,可以發現,確實存在不穩定現象。
參數(特征)的不穩定,影響了梯度,接著又反過來影響參數更新。最終這個過程對性能有較大的不良干擾的風險。因此需要想辦法去控制這種不穩定性。
進一步的,對于擴散模型。UNet的輸入是一個帶噪圖像,如果要求模型能從中準確預測出加入的噪聲,這需要模型對輸入有很強的抵御額外擾動的魯棒性。

論文:https://arxiv.org/abs/2310.13545
代碼:https://github.com/sail-sg/ScaleLong
研究人員發現上述這些問題,可以在Long skip connection上進行Scaling來進行統一地緩解。
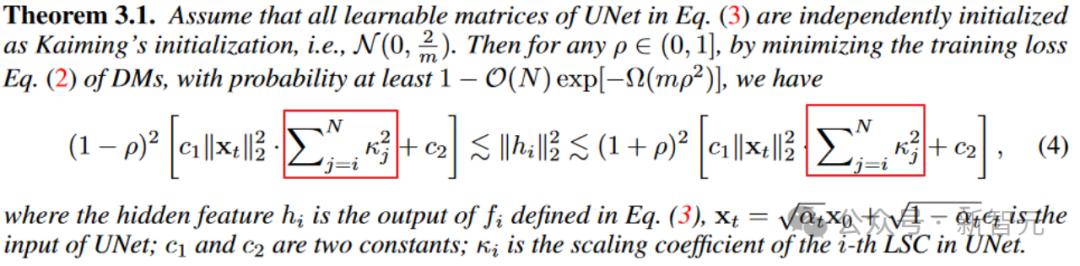
從定理3.1來看,中間層特征的震蕩范圍(上下界的寬度)正相關于scaling系數的平方和。適當的scaling系數有助于緩解特征不穩定。
不過需要注意的是,如果直接讓scaling系數設置為0,確實最佳地緩解了震蕩。(手動狗頭)
但是UNet退化為無skip的情況的話,不穩定問題是解決了,但是表征能力也沒了。這是模型穩定性和表征能力的trade-off。
 圖片
圖片
類似地,從參數梯度的角度。定理3.3也揭示了scaling系數對梯度量級的控制。
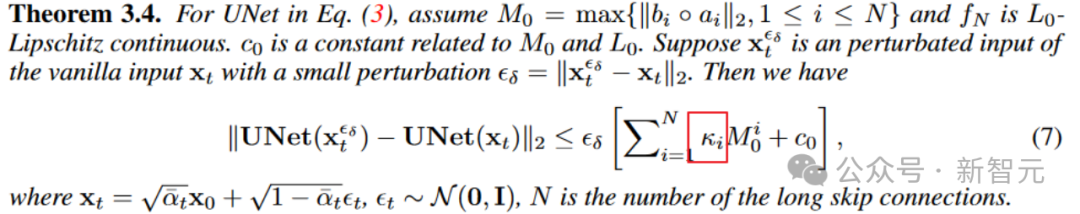 圖片
圖片
進一步地,定理3.4還揭示了long skip connection上的scaling還可以影響模型對輸入擾動的魯棒上界,提升擴散模型對輸入擾動的穩定性。
成為Scaling
通過上述的分析,我們清楚了Long skip connection上進行scaling對穩定模型訓練的重要性,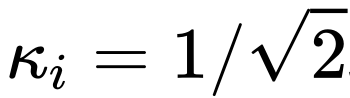 也適用于上述的分析。
也適用于上述的分析。
接下來,我們將分析怎么樣的scaling可以有更好的性能,畢竟上述分析只能說明scaling有好處,但不能確定怎么樣的scaling最好或者較好。
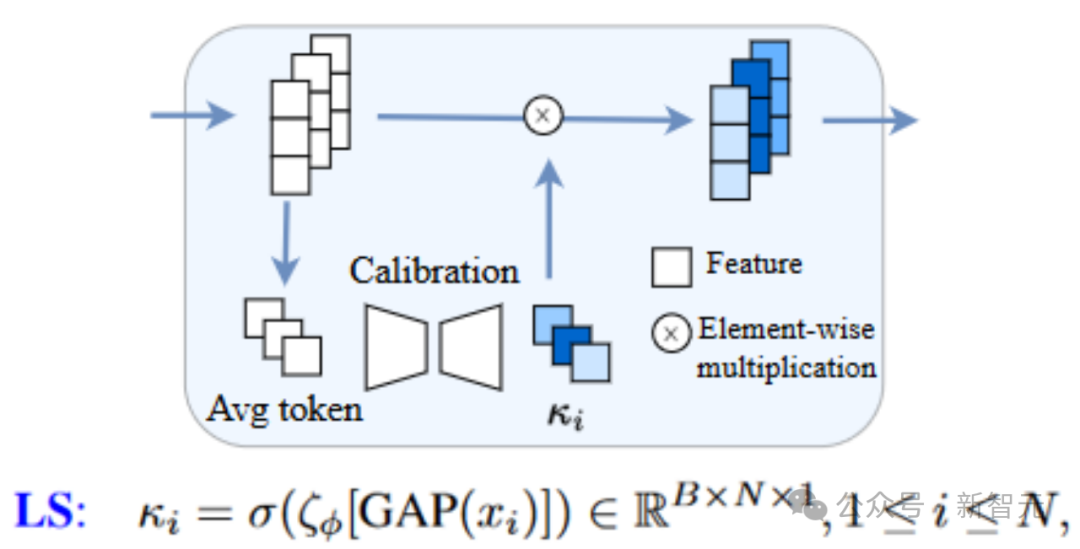
一種簡單的方式是為long skip connection引入可學習的模塊來自適應地調整scaling,這種方法稱為Learnable Scaling (LS) Method。我們采用類似SENet的結構,即如下所示(此處考慮的是代碼整理得非常好的U-ViT結構,贊!)
 圖片
圖片
從本文的結果來看,LS確實可以有效地穩定擴散模型的訓練!進一步地,我們嘗試可視化LS中學習到的系數。
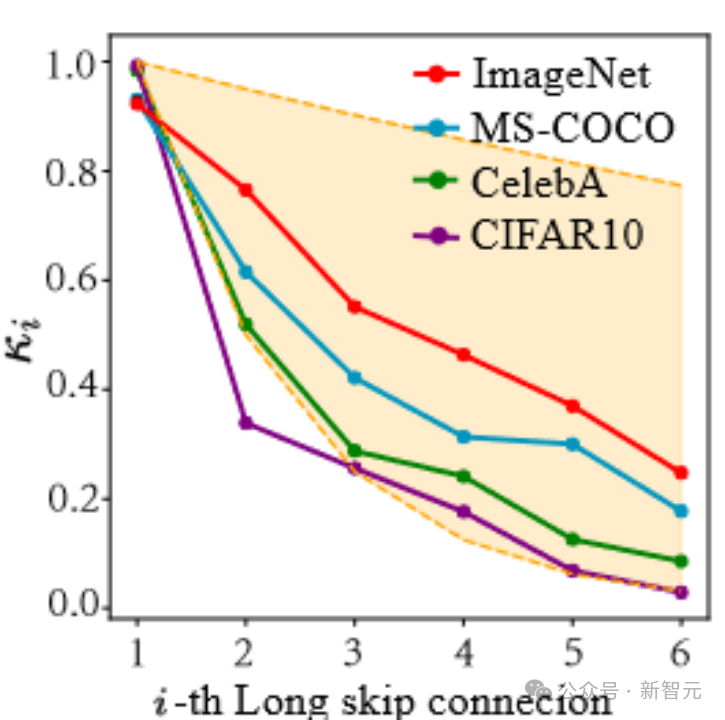
如下圖所示,我們會發現這些系數呈現出一種指數下降的趨勢(注意這里第一個long skip connection是指連接UNet首尾兩端的connection),且第一個系數幾乎接近于1,這個現象也很amazing!
 圖片
圖片
基于這一系列觀察(更多的細節請查閱論文),我們進一步提出了Constant Scaling (CS) Method,即無需可學習參數的:
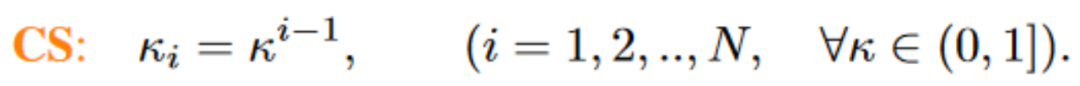
CS策略和最初的使用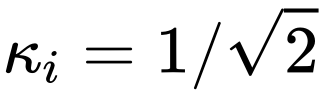 的scaling操作一樣無需額外參數,從而幾乎沒有太多的額外計算消耗。
的scaling操作一樣無需額外參數,從而幾乎沒有太多的額外計算消耗。
雖然CS在大多數時候沒有LS在穩定訓練上表現好,不過對于已有的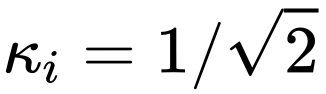 策略來說,還是值得一試。
策略來說,還是值得一試。
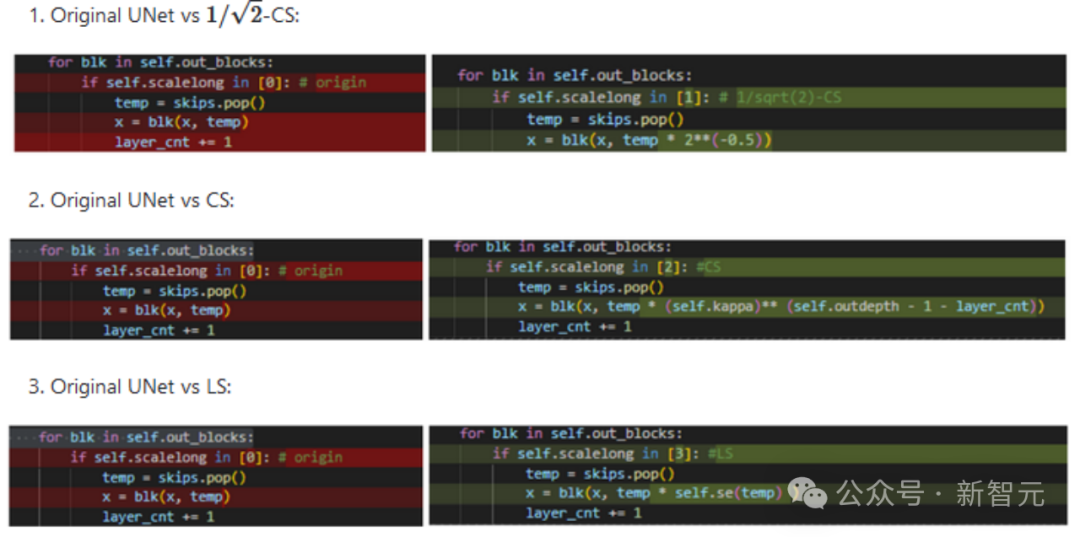
上述CS和LS的實現均非常簡潔,僅僅需要若干行代碼即可。針對各(hua)式(li)各(hu)樣(shao)的UNet結構可能需要對齊一下特征維度。(手動狗頭+1)
最近,一些后續工作,比如FreeU、SCEdit等工作也揭示了skip connection上scaling的重要性,歡迎大家試用和推廣。