機器學習的最優化算法是用于找到最佳模型參數，以最小化預測誤差的算法。這些算法通過迭代地調整模型參數，以不斷改進模型的性能。

本文系統地介紹了優化算法，基本脈絡是從優化的基礎知識，到各種優化算法原理的介紹及代碼示例，最后放上各種算法的對比及實踐經驗總結!

一、基礎知識

1.1 梯度(一階導數)

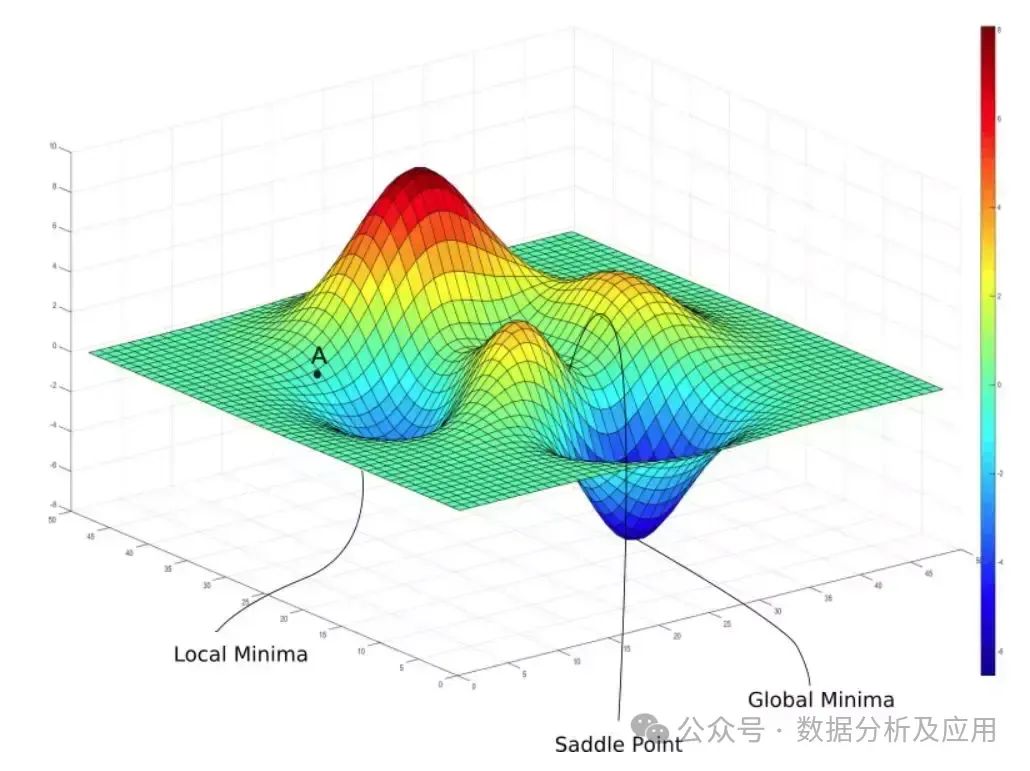
考慮一座在 (x1, x2) 點高度是 f(x1, x2) 的山。那么，某一點的梯度方向是在該點坡度最陡的方向，而梯度的大小告訴我們坡度到底有多陡。注意，梯度也可以告訴我們不在最快變化方向的其他方向的變化速度(二維情況下，按照梯度方向傾斜的圓在平面上投影成一個橢圓)。對于一個含有 n 個變量的標量函數，即函數輸入一個 n 維 的向量，輸出一個數值，梯度可以定義為：

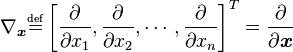
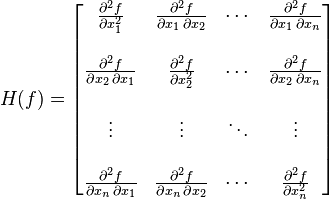
1.2 Hesse 矩陣(二階導數)

Hesse 矩陣常被應用于牛頓法解決的大規模優化問題(后面會介紹)，主要形式如下：

當 f(x) 為二次函數時，梯度以及 Hesse 矩陣很容易求得。二次函數可以寫成下列形式：

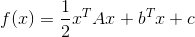
其中 A 是 n 階對稱矩陣，b 是 n 維列向量， c 是常數。f(x) 梯度是 Ax+b, Hesse 矩陣等于 A。

1.3 Jacobi 矩陣

Jacobi 矩陣實際上是向量值函數的梯度矩陣，假設F:Rn→Rm 是一個從n維歐氏空間轉換到m維歐氏空間的函數。這個函數由m個實函數組成:

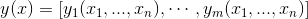
。這些函數的偏導數(如果存在)可以組成一個m行n列的矩陣(m by n)，這就是所謂的雅可比矩陣：

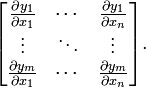
二、機器學習的優化算法

2.1 梯度下降法(Gradient Descent)

梯度下降法是最常用的一種優化算法，通過迭代地沿著梯度的負方向來尋找最優解。

在機器學習中，梯度下降法通常用于求解損失函數的最小值，通過不斷更新模型的參數來逐漸減小損失函數的值。

梯度下降法的優點是簡單、穩定且容易實現，適用于大規模數據集和復雜的模型。

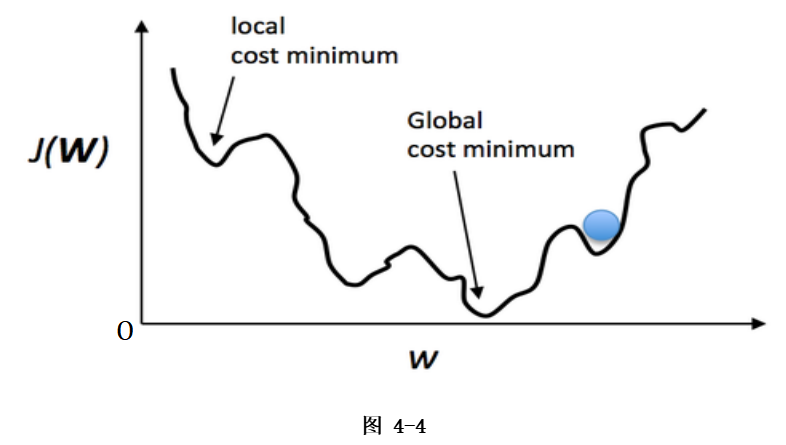
梯度下降是一個大類，常見的梯度下降類算法如下圖：

2.2 隨機梯度下降法(Stochastic Gradient Descent, SGD)

隨機梯度下降是在梯度下降算法效率上做了優化，不使用全量樣本計算當前的梯度，而是使用小批量(mini-batch)樣本來估計梯度，大大提高了效率。

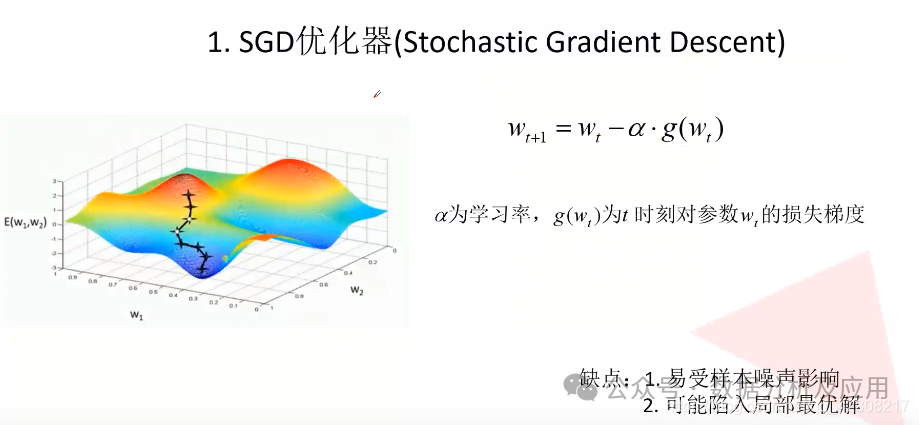
原因在于使用更多樣本來估計梯度的方法的收益是低于線性的，對于大多數優化算法基于梯度下降，如果每一步中計算梯度的時間大大縮短，則它們會更快收斂。且訓練集通常存在冗余，大量樣本都對梯度做出了非常相似的貢獻。此時基于小批量樣本估計梯度的策略也能夠計算正確的梯度，但是節省了大量時間。

SGD具有快速收斂的特點，適用于處理大規模數據集和分布式計算環境。

SGD的缺點是容易陷入局部最優解，可結合其他優化算法如動量法或Adam等來提高收斂效果。

import numpy as np  
  
# 定義損失函數  
def loss_function(w, X, y):  
    return np.sum(np.square(X.dot(w) - y)) / len(y)  
  
# 定義梯度函數  
def gradient(w, X, y):  
    return X.T.dot((X.dot(w) - y)) / len(y)  
  
# 定義SGD優化器  
def sgd(X, y, learning_rate=0.01, epochs=100):  
    n_features = X.shape[1]  
    w = np.zeros(n_features)  
    for epoch in range(epochs):  
        for i in range(len(X)):  
            grad = gradient(w, X[i], y[i])  
            w -= learning_rate * grad  
        print("Epoch %d loss: %f" % (epoch+1, loss_function(w, X, y)))  
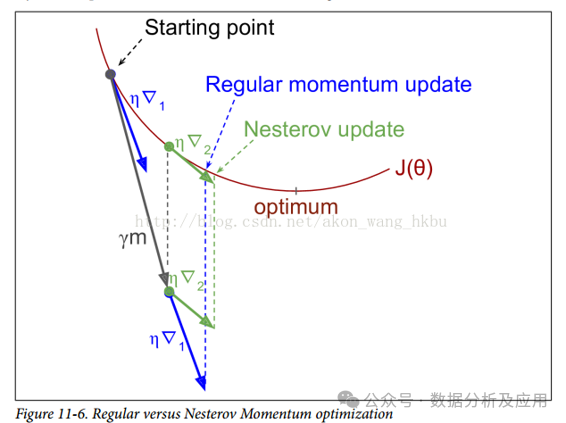
    return w

2.3 動量法(Momentum)和Nesterov 動量法

動量法通過引入一個動量項來加速梯度下降法的收斂速度。

Nesterov 動量法是對動量法的改進，在每一步迭代中考慮了未來的信息，從而更好地指導參數的更新方向。

動量法和Nesterov 動量法適用于非凸優化問題，能夠跳出局部最優解并加速收斂。

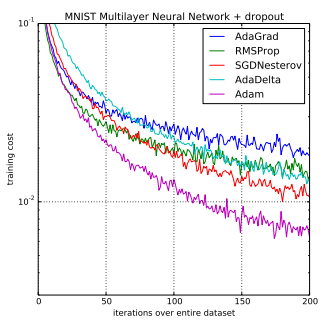
2.4 Adam(Adaptive Moment Estimation)

Adam是最常用的優化算法之一，是一種自適應學習率的優化算法，結合了動量法和RMSprop的思想。

Adam能夠自動調整學習率，并且在不同的數據分布和模型結構下具有良好的收斂效果。(雖然說已經簡化了調參，但是并沒有一勞永逸地解決問題，默認的參數雖然好，但也不是放之四海而皆準。因此，在充分理解數據的基礎上，依然需要根據數據特性、算法特性進行充分的調參實驗。)

Adam適用于處理高維特征和稀疏數據集，非常適用于深度學習模型中的參數優化。在使用大型模型和數據集的情況下，Adam 優化算法在解決局部深度學習問題上是很高效的。

import torch  
import torch.optim as optim  
import numpy as np  
  
# 定義損失函數和梯度函數（這里使用PyTorch的自動梯度計算）  
loss_function = torch.nn.MSELoss()  # 均方誤差損失函數  
gradient = torch.autograd.grad  # 自動梯度計算函數  
  
# 定義Adam優化器（這里使用了PyTorch的Adam類）  
optimizer = optim.Adam([torch.Tensor([0.])], lr=0.01)  # 學習率設置為0.01，初始權重為0向量（注意：PyTorch中優化器的權重參數需要是tensor對象）  
optimizer.zero_grad()  # 清除歷史梯度信息（如果使用其他優化器，可能需要手動清除梯度）  
output = loss_function(torch.Tensor([1]), torch.Tensor([[1, 2], [3, 4]]), torch.Tensor([[2], [4]]))  # 計算損失函數值（這里使用了PyTorch的Tensor類，模擬了線性回歸問題的數據和目標）  
output.backward()  # 反向傳播計算梯度（這里使用了PyTorch的backward方法）  
optimizer.step()  # 更新權重（這里使用了PyTorch的step方法）

2.5 AdaGrad(Adaptive Gradient Algorithm)和RMSprop

AdaGrad是一種自適應學習率的優化算法，能夠根據參數的歷史梯度來動態調整學習率。

RMSprop則是對AdaGrad的改進，通過引入一個指數衰減的平均來平滑歷史梯度的方差。

AdaGrad和RMSprop適用于處理稀疏數據集和具有非平穩目標函數的優化問題。

2.6 牛頓法(Newton's Method)和擬牛頓法(Quasi-Newton Methods)

牛頓法是一種基于目標函數的二階導數信息的優化算法，通過構建二階導數矩陣并對其進行求解來逼近最優解。

擬牛頓法是牛頓法的改進，通過構造一個對稱正定的矩陣來逼近目標函數的二階導數矩陣的逆矩陣，從而避免了直接計算二階導數矩陣的逆矩陣。

牛頓法和擬牛頓法適用于二階可導的目標函數，具有較快的收斂速度，但在計算二階導數矩陣時需要較大的存儲空間。

import numpy as np  
from scipy.linalg import inv  
  
# 定義損失函數和Hessian矩陣  
def loss_function(w, X, y):  
    return np.sum(np.square(X.dot(w) - y)) / len(y)  
  
def hessian(w, X, y):  
    return X.T.dot(X) / len(y)  
  
# 定義牛頓法優化器  
def newton(X, y, learning_rate=0.01, epochs=100):  
    n_features = X.shape[1]  
    w = np.zeros(n_features)  
    for epoch in range(epochs):  
        H = hessian(w, X, y)  
        w -= inv(H).dot(gradient(w, X, y))  
        print("Epoch %d loss: %f" % (epoch+1, loss_function(w, X, y)))  
    return w

2.7 共軛梯度法(Conjugate Gradient)

共軛梯度法是介于梯度下降法和牛頓法之間的一種方法，利用共軛方向進行搜索。

共軛梯度法的優點是在每一步迭代中不需要計算完整的梯度向量，而是通過迭代的方式逐步逼近最優解。

該方法適用于大規模問題，尤其是稀疏矩陣和對稱正定的問題。

2.8 LBFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno)

一種有限內存的Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法，主要用于解決大規模優化問題。由于它只需要有限數量的計算機內存，因此特別適合處理大規模問題。LBFGS算法的目標是最小化一個給定的函數，通常用于機器學習中的參數估計。

import numpy as np  
from scipy.optimize import minimize  
  
# 目標函數  
def objective_function(x):  
    return x**2 - 4*x + 4  
  
# L-BFGS算法求解最小值  
result = minimize(objective_function, x0=1, method='L-BFGS-B')  
x_min = result.x  
print(f"L-BFGS的最小值為：{objective_function(x_min)}")

2.9 SA(Simulated Annealing)

一種隨機搜索算法，其靈感來源于物理退火過程。該算法通過接受或拒絕解的移動來模擬退火過程，以避免陷入局部最優解并尋找全局最優解。在模擬退火算法中，接受概率通常基于解的移動的優劣和溫度的降低，允許在搜索過程中暫時接受較差的解，這有助于跳出局部最優，從而有可能找到全局最優解。

import numpy as np  
from scipy.optimize import anneal  
  
# 目標函數  
def objective_function(x):  
    return (x - 2)**2  
  
# SA算法求解最小值  
result = anneal(objective_function, x0=0, lower=-10, upper=10, maxiter=1000)  
x_min = result.x  
print(f"SA的最小值為：{objective_function(x_min)}")

2.10 AC-SA(Adaptive Clustering-based Simulated Annealing)

一種基于自適應聚類的模擬退火算法。通過模擬物理退火過程，利用聚類技術來組織解空間并控制解的移動。該方法適用于處理大規模、高維度的優化問題，尤其適用于那些具有多個局部最優解的問題。

遺傳算法是一種基于自然選擇和遺傳學機理的生物進化過程的模擬算法，適用于解決優化問題，特別是組合優化問題。該算法通過數學的方式，利用計算機仿真運算，將問題的求解過程轉換成類似生物進化中的染色體基因的交叉、變異等過程。在求解較為復雜的組合優化問題時，相對一些常規的優化算法，通常能夠較快地獲得較好的優化結果。

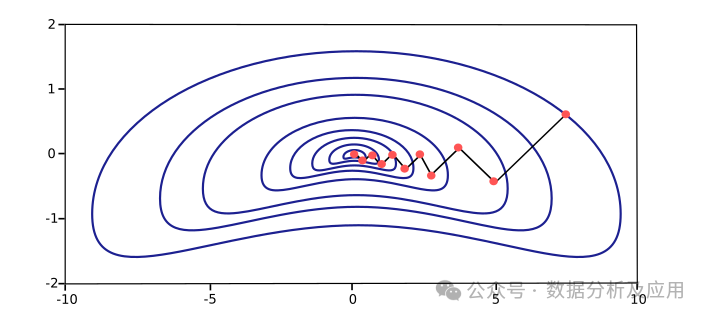
2.11 PSO(Particle Swarm Optimization)

PSO是一種基于種群的隨機優化技術，模擬了鳥群覓食的行為(吐槽下，智能優化算法的領域真是卷麻了!!!)。粒子群算法模仿昆蟲、獸群、鳥群和魚群等的群集行為，這些群體按照一種合作的方式尋找食物，群體中的每個成員通過學習它自身的經驗和其他成員的經驗來不斷改變其搜索模式。PSO算法適用于處理多峰函數和離散優化問題，具有簡單、靈活和容易實現的特點。

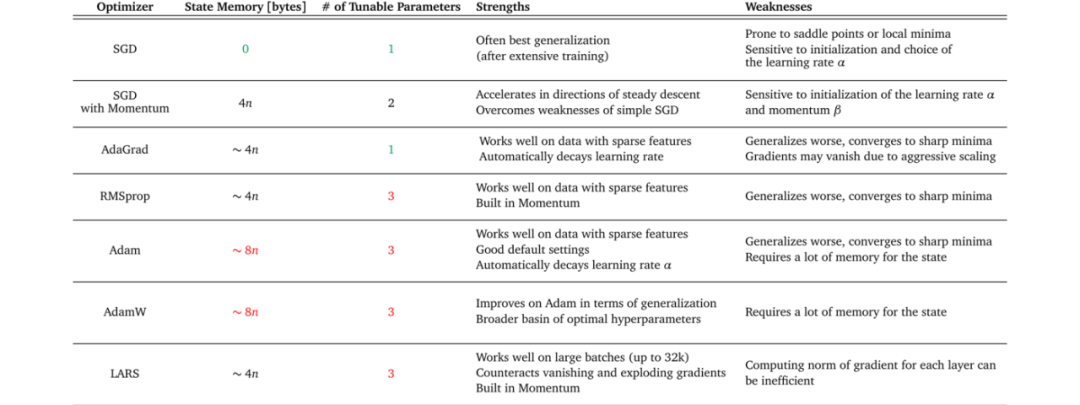
回顧下各類算法的優缺點：

• 梯度下降類的優化算法：優點是簡單、快速，常用于深度神經網絡模型;缺點是可能得到的是局部最優解。
• 牛頓法：優點是二階收斂，收斂速度快;缺點是需要計算目標函數的Hessian矩陣，計算復雜度高。
• 模擬退火算法：優點是避免陷入局部最優解，能夠找到全局最優解;缺點是收斂速度慢，需要大量時間。
• 遺傳算法：優點是通過變異機制避免陷入局部最優解，搜索能力強;缺點是編程復雜，需要設置多個參數，實現較為復雜。
• 粒子群優化算法：優點是簡單、收斂快、計算復雜度低;缺點是多樣性丟失、容易陷入局部最優，實現較為復雜。

三、優化算法的小結

本文介紹了梯度下降類、牛頓法、模擬退火、遺傳算法和粒子群優化等常用的機器學習優化算法。這些算法各有特點和適用范圍，選擇合適的算法需要根據具體的問題、數據集和模型來進行權衡的。

最后，結合經驗分享一些常用梯度下降類優化算法的選擇和使用技巧：

首先，沒有一種算法是普遍適用于所有情況的。如果你是初學者，建議從SGD+Nesterov Momentum或Adam開始。

選擇你熟悉的算法，這樣你可以更熟練地調整參數并利用經驗。

充分了解你的數據。如果模型非常稀疏，優先考慮使用自適應學習率的算法。

根據你的需求選擇算法。在模型設計實驗階段，為了快速驗證新模型的效果，可以使用Adam進行快速實驗優化。在模型上線或發布之前，使用經過微調的SGD進行模型的精細優化。

先用小數據集進行實驗。有研究指出，隨機梯度下降算法的收斂速度與數據集的大小關系不大。因此，可以使用具有代表性的小數據集進行實驗，測試最佳優化算法，并通過參數搜索找到最優的訓練參數。

考慮不同算法的組合。先用Adam進行快速下降，然后再切換到SGD進行充分調優。切換策略可以參考本文介紹的方法。

確保數據集充分打散(shuffle)。這樣在使用自適應學習率算法時，可以避免某些特征集中出現，導致學習過度或不足，使下降方向出現偏差。

在訓練過程中持續監控訓練數據和驗證數據上的目標函數值以及精度或AUC等指標的變化情況。對訓練數據的監控是為了確保模型進行了充分訓練——下降方向正確且學習率足夠高。對驗證數據的監控是為了避免過擬合。

制定合適的學習率衰減策略。可以使用定期衰減策略，例如每過幾個epoch就衰減一次;或者利用精度或AUC等性能指標進行監控。當測試集上的指標不再改善或下降時，降低學習率。