機器學習:K均值算法
一、基礎理論
1. 歐氏距離
想象你在北京,想要知道離上海有多遠,則可以直接計算這個城市(兩點)間直線的距離,這就是歐氏距離。
在二維平面上,在二維平面上有兩個點A(x1, y1)和B(x2, y2),歐氏距離為:
 圖片
圖片
歐氏距離衡量的是兩點間的真實物理距離,關注的是位置的絕對差異。
2. 曼哈頓距離
想象你在曼哈頓,你想從一個街區走到另外一個街區。你不能走直線,只能沿著街道走,橫著走一條街,再豎著走一條街,所行走的路徑長度就是曼哈頓距離。
在二維平面上,在二維平面上有兩個點A(x1, y1)和B(x2, y2),曼哈頓距離就是:
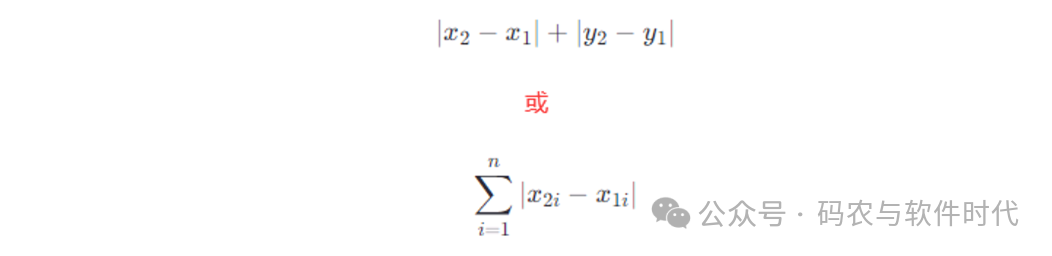 圖片
圖片
曼哈頓距離考慮的是在各個維度上的絕對差值之和,適用于那些移動只能沿坐標軸進行的情況。
3. 切比雪夫距離
想象你在一個方格化的城市里,每個路口都嚴格地按照東西南北四個方向排列,就像一個巨大的棋盤。
你現在在一個交叉口,想要去往另一個交叉口,你可以是直行、左轉、右轉、走對角線(盡管現實中不能這么走),但每次只能走一個街區。
在所有可能的路線中,街區數最大的路線所對應的距離就是切比雪夫距離。
假如在二維平面上有兩個點A(x1, y1)和B(x2, y2),切比雪夫距離的公式為:
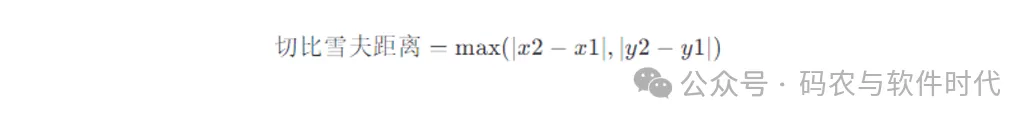
4. 閔可夫斯基距離
假設我們要比較兩個點A和B,在n維空間中的坐標分別為
 圖片
圖片
則閔可夫斯基距離的計算公式是:
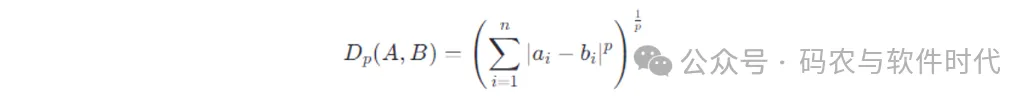 圖片
圖片
參數??取不同的值時,則就變成了不同的距離:
- 當??=1時,為曼哈頓距離。
- 當??=2時,為歐式距離。
- 當??趨近于無窮大時,為切比雪夫距離。
5. 余弦相似度
余弦相似度是一種衡量兩個向量方向相似性的方法。
想象在三維空間有兩個向量,一個指向東,另一個指向東北,這兩個向量指向角度的接近程度就是余弦相似度。
如果兩個向量指向完全相同的方向,相似度為1(即它們的夾角為0度);如果指向完全相反,相似度為-1(180度);如果它們垂直,則相似度為0。
余弦相似度的計算公式:
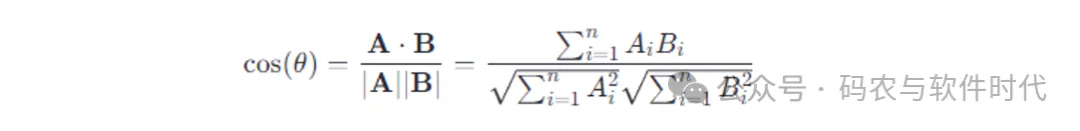 圖片
圖片
兩個向量的點積除以它們各自的長度(模)的乘積。
6. 值差異度量
在討論距離計算時,特征是要直接比較大小的。
對于連續數值可以直接進行大小比較,如高度、溫度、成績等。
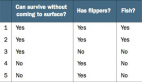
而對于離散特征,又有可以直接比較大小,如教育程度(小學、中學、大學)、服裝尺碼(S、M、L、XL)等;還有不可以直接比較大小的,如顏色(紅、綠、藍)、國籍(中國、美國、日本)等。
對于不可以直接比較大小的離散特征(離散無序),可以使用值差異度量(Value Difference Metric,VDM)。
VDM的核心思想是離散無序的數據轉化為可以量化的差異度量,以進行比較和分析。具體步驟為:
(1)權重分配
A. 頻率倒數法:
- 計算頻率:對于每個無序特征,統計每個特征值在整個數據集中出現的次數,并計算出頻率(出現次數/總樣本數)。
- 計算權重:使用頻率的倒數或其變形來作為權重。這是因為,頻率較高的屬性值(即較為常見的值)往往提供較少的區分信息,因此給予較小的權重;反之,頻率較低的屬性值(罕見值)提供較多區分信息,應給予較高權重。計算公式如 wi=1/fi+?,其中 fi 是特征值i的頻率,? 是一個很小的正數(如1e-6),用于防止頻率為0時,導致分母為0無法計算的問題。
B. 信息熵或信息增益。
對于兩個具體的值 va 和 vb,它們之間的值差異 D(va,vb) 可以直接根據它們的權重 wa 和 wb 計算。如果 va=vb,則差異為0;如果 va不等于vb,差異通常定義為 ∣wa?wb∣。
如果一個樣本由多個無序特征組成,比如對象=(特征1,特征2,...,特征??) ,那么可以對每個特征應用上述差異計算方法,然后將所有特征的差異值相加或取平均),以獲得兩個樣本之間的總距離或相似度得分。
假設有一家電商平臺想通過分析顧客的購物記錄,來發現不同的消費群體。顧客數據包含以下幾個無序特征:
(1)性別:男、女。
(2)地區:北京、上海、廣州、深圳、其他。
(3)商品類別偏好:電子產品、家居用品、服飾、圖書、食品。
VDM計算的過程為:
(1)數據預處理與權重計算
A. 統計頻率
- 性別:男(52%),女(48%)
- 地區:北京(25%),上海(29%),廣州(18%),深圳(15%),其他(13%)
- 商品類別偏好:電子產品(30%),家居用品(22%),服飾(25%),圖書(10%),食品(13%)
B. 計算權重
- 假設采用頻率倒數法,加入一個微小常數 ?=0.001 。
性別:男(1/0.52 + 0.001)= 1.93, 女(1/0.48 + 0.001)= 2.08。
地區:北京(1/0.25 + 0.001)= 4.04, 上海(1/0.29 + 0.001)= 3.45, 廣州(1/0.18 + 0.001)= 5.59, 深圳(1/0.15 + 0.001)= 6.69, 其他(1/0.13 + 0.001)= 7.69。
商品類別偏好:電子產品(1/0.30 + 0.001)= 3.34, 家居用品(1/0.22 + 0.001)= 4.57, 服飾(1/0.25 + 0.001)= 4.04, 圖書(1/0.10 + 0.001)= 10.01, 食品(1/0.13 + 0.001)= 7.69。
(2)應用VDM:利用上面計算的權重計算兩個顧客間的距離,以進行聚類。
- 假設有兩位顧客A和B,A的屬性為(男,上海,電子產品),B的屬性為(女,北京,圖書)。
- 使用VDM計算差異:性別差異 = |1.93 - 2.08| = 0.15;地區差異 = |4.04 - 3.45| = 0.59;商品類別偏好差異 = |3.34 - 10.01| = 6.67。
- 合并差異:總距離 = 0.15 + 0.59 + 6.67 = 7.41。
二、聚類算法
聚類算法是一種無監督學習方法,其主要目的是將一組未標記的數據集分割成多個子集,稱為簇(Clusters)。也就是聚類算法并不依賴于預先定義的類別標簽,而是通過分析數據本身的特征和結構,自動發現數據中的隱藏模式或群組。
聚類算法的基本思想是基于相似性度量(如歐氏距離、余弦相似性等)來量化數據點之間的相似度,并利用這些度量來優化某個目標函數,從而實現數據的分組。
聚類算法可以根據不同的原則和策略進行分類,主要有:
(1)劃分聚類(Partitioning Clustering):將數據集劃分為預先指定數量的簇,每個數據點只能屬于一個簇。最典型的例子是K-means算法。
(2)層次聚類(Hierarchical Clustering):可以進一步細分為凝聚型(Agglomerative)和分裂型(Divisive)。凝聚型算法從每個數據點作為一個獨立的簇開始,然后逐步合并最相似的簇,直到滿足某個終止條件;而分裂型則相反,開始時將所有數據視為一個簇,然后逐漸分裂。常見的算法有AGNES(Agglomerative Nesting)、DIANA(Divisive Analysis)、BIRCH等。
(3)基于密度的聚類(Density-Based Clustering):基于數據點的鄰域密度來確定簇,能夠處理形狀不規則的簇和含有噪聲的數據。DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是最知名的算法之一,它通過設置鄰域半徑和最小點數來識別高密度區域。OPTICS、DENCLUE也是基于密度的算法。
(4)基于網格的聚類(Grid-Based Clustering):將數據空間劃分為多個單元或網格,然后在網格層次上進行聚類。STING(Statistical Information Grid-based Clustering)、WaveCluster、CLIQUE(Clustering in Quest)是典型代表,它們適合處理大規模空間數據庫。
(5)基于模型的聚類(Model-Based Clustering):假設數據由某些數學模型(如高斯分布)生成,并嘗試找到最佳的模型參數來描述數據。高斯混合模型(GMM, Gaussian Mixture Model)是最常見的例子,它通過最大似然估計來擬合數據到多個高斯分布上。
三、K-means算法
K-means算法是一種將數據集劃分為K個互不相交的子集(簇),使得同一簇內的數據點彼此相似,而不同簇的數據點相異。
K-means(均值)算法的基本操作過程為:
1. 初始設置
(1)數據集:假設我們有一個二維數據集,包含以下五個數據點:{X(1, 2), Y(2, 1), Z(4, 8), W(5, 9), V(6, 7)}。
(2)初始化質心:隨機選擇兩個數據點作為初始聚類中心(質心):C1(2, 3), C2(6, 7)。
2. 執行步驟
步驟1: 數據點分配
- 對于數據集中的每個數據點,計算到C1和C2的距離。
 圖片
圖片
- 將每個數據點分配給距離最近的質心所在的簇。
假設結果為:
C1簇: {X(1, 2), Y(2, 1)}
C2簇: {Z(4, 8), W(5, 9), V(6, 7)}
步驟2: 更新質心
 圖片
圖片
步驟3: 迭代與收斂判斷
- 重復步驟1和步驟2,直到質心的移動距離小于某個預設的閾值或達到預定的迭代次數。這一步確保算法收斂于一個穩定的聚類結果。
需要注意的是:
(1)初始質心選擇:K-means算法對初始質心的選擇敏感,不同的初始質心可能導致不同的聚類結果。
(2)簇形狀:K-means假設簇為凸形狀,可能不適合處理復雜的數據分布,如密度不均或存在異常點的情況。
(3)K值選擇:選擇合適的K值是關鍵,常用方法有肘部法則(Elbow Method)和輪廓系數法等。