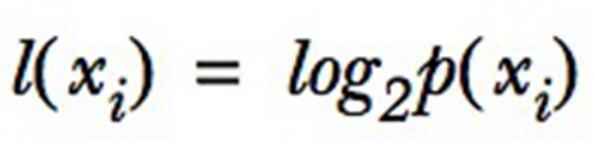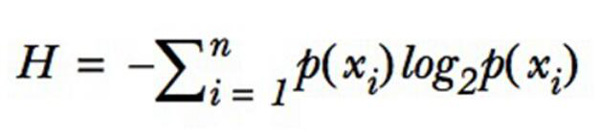機器學習決策樹算法學習筆記
基本概念
決策樹是分類算法。
數據類型:數值型和標稱型。因為構造算法只適用于標稱型,所以數值型數據必須離散化。
工作原理
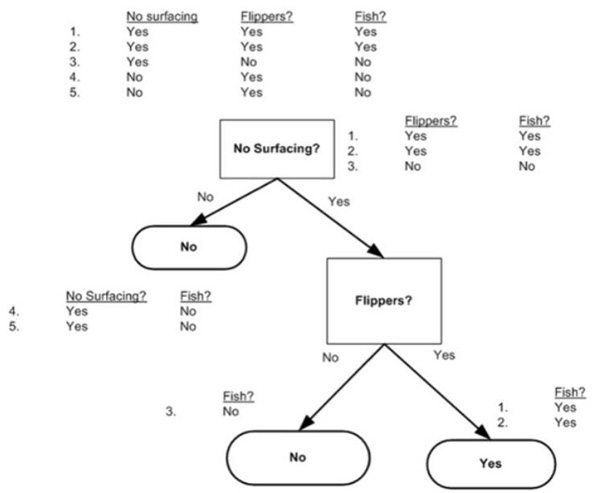
利用香濃熵找到信息增益***的特征,按照信息增益***的特征劃分數據,如此反復,讓無序的數據變的更加有序。使用ID3算法構建樹結構。當傳入一個新數據時,按照數據找到對應樹節點,直到***沒有葉子節點時,完成分類。
樣例
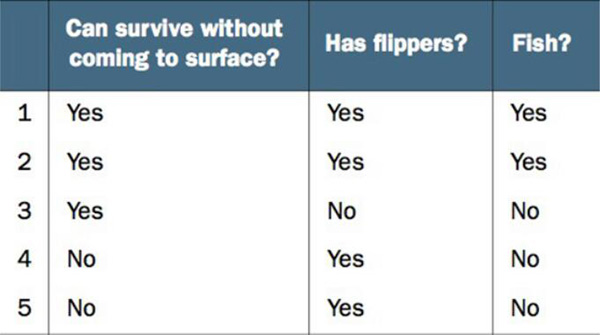
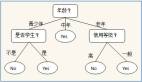
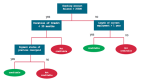
不浮出水面是否可以生存? 是否有腳蹼? 是否是魚類?
通過“不浮出水面是否可以生存”和“是否有腳蹼”這兩個特征來判斷是否是魚類。構建一個簡單決策樹,如果得到一個新的生物,可以用此來判斷是否是魚類。
樣例代碼
- def createDataSet():
- dataSet = [[1, 1, 'yes'],
- [1, 1, 'yes'],
- [1, 0, 'no'],
- [0, 1, 'no'],
- [0, 1, 'no']]
- labels = ['no surfacing','flippers']
- return dataSet, labels
香農熵公式
如果待分類的事務可能劃分在多個分類之中,則符號Xi的信息定義為:
其中P(Xi)是選擇該分類的概率
為了計算熵,需要計算所有類別所有可能值包含的信息期望值總和,公式為:
其中n是分類的數目
香農熵算法
- def calcShannonEnt(dataSet):
- # 選擇該分類的概率 就是每個類型/總個數
- # 總數,多少行數據
- numEntries = len(dataSet)
- labelCounts = {}
- # 取到的每個類型個數
- for featVec in dataSet:
- currentLabel = featVec[-1]
- if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
- labelCounts[currentLabel] += 1
- shannonEnt = 0.0
- for key in labelCounts:
- # 得到選擇該分類的概率
- prob = float(labelCounts[key])/numEntries
- # 按照公式
- shannonEnt -= prob * log(prob,2) #log base 2
- return shannonEnt
按照香農熵劃分數據
除了需要測量信息熵,還需要劃分數據集,度量花費數據集的熵,以便判斷當前是否正確劃分。 循環計算香濃熵和splitDataSet(),找到***的特征劃分方式。
- def splitDataSet(dataSet, axis, value):
- # 這個算法返回axis下標之外的列
- retDataSet = []
- for featVec in dataSet:
- if featVec[axis] == value:
- reducedFeatVec = featVec[:axis] #chop out axis used for splitting
- reducedFeatVec.extend(featVec[axis+1:])
- retDataSet.append(reducedFeatVec)
- return retDataSet
- def chooseBestFeatureToSplit(dataSet):
- # 先取***一列,用在標簽結果:是魚或不是魚。
- numFeatures = len(dataSet[0]) - 1
- # 原始香濃熵
- baseEntropy = calcShannonEnt(dataSet)
- bestInfoGain = 0.0; bestFeature = -1
- # 遍歷所有的特征
- for i in range(numFeatures):
- # 創建一個列表包含這個特征的所有值
- featList = [example[i] for example in dataSet]
- # 利用set去重
- uniqueVals = set(featList)
- newEntropy = 0.0
- # 計算該特征所包含類型的香濃熵之和
- for value in uniqueVals:
- subDataSet = splitDataSet(dataSet, i, value)
- prob = len(subDataSet)/float(len(dataSet))
- newEntropy += prob * calcShannonEnt(subDataSet)
- # 得到信息增益
- infoGain = baseEntropy - newEntropy
- # 取***的信息增益,并記錄下標
- if (infoGain > bestInfoGain):
- bestInfoGain = infoGain
- bestFeature = i
- # 返回下標
- return bestFeature
數據集需要滿足一定的要求:
- 數據必須是一種有列表元素組成的列表。(二維數組)
- 所有列表元素必須有相同長度。
- ***一列必須是當前實例的標簽。
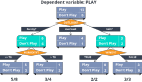
遞歸構建決策樹
多數表決算法
如果數據集已經處理了所有屬性,但是類標簽依然不是唯一的,此時需要決定如何定義該葉子節點,在這種情況下,我們通常會采用多數表決決定該葉子節點。
- import operator
- def majorityCnt(classList):
- # 排序取出種類最多的
- classCount={}
- for vote in classList:
- if vote not in classCount.keys(): classCount[vote] = 0
- classCount[vote] += 1
- sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
- return sortedClassCount[0][0]
構建樹算法
- def createTree(dataSet,labels):
- # 取出結果
- classList = [example[-1] for example in dataSet]
- # 如果結果里的***個元素所代表的數據個數等于結果本身,說明沒有其他分類了
- if classList.count(classList[0]) == len(classList):
- return classList[0]
- # 如果沒有更多數據了,超過一個才有分類的意義
- if len(dataSet[0]) == 1:
- # 多數表決,返回出現次數最多的
- return majorityCnt(classList)
- # 選出最適合用于切分類型的下標
- bestFeat = chooseBestFeatureToSplit(dataSet)
- # 根據下標取出標簽
- bestFeatLabel = labels[bestFeat]
- # 構建樹
- myTree = {bestFeatLabel:{}}
- # 刪除取出過的標簽,避免重復計算
- del(labels[bestFeat])
- featValues = [example[bestFeat] for example in dataSet]
- # 利用set去重
- uniqueVals = set(featValues)
- for value in uniqueVals:
- # 復制所有的子標簽,因為是引用類型,以避免改變原始標簽數據
- subLabels = labels[:]
- # 遞歸的構建樹
- myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
- return myTree
使用決策樹分類
- def classify(inputTree,featLabels,testVec):
- firstStr = inputTree.keys()[0]
- secondDict = inputTree[firstStr]
- featIndex = featLabels.index(firstStr)
- # print 'featIndex %s' % (featIndex)
- key = testVec[featIndex]
- # print 'key %s' % (key)
- valueOfFeat = secondDict[key]
- if isinstance(valueOfFeat, dict):
- classLabel = classify(valueOfFeat, featLabels, testVec)
- else: classLabel = valueOfFeat
- return classLabel
- dataSet, labels = createDataSet()
- mytree = createTree(dataSet, labels[:]) #因為內部會刪除labels里的值所以用這樣copy一份
- print mytree
- # {'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
- print classify(mytree, labels, [0,1])
- no
決策樹的存儲
構造決策樹是耗時的任務,即使處理很小的數據集。所以我們可以使用構造好的決策樹。
- def storeTree(inputTree,filename):
- import pickle
- fw = open(filename,'w')
- pickle.dump(inputTree,fw)
- fw.close()
- def grabTree(filename):
- import pickle
- fr = open(filename)
- return pickle.load(fr)
優點
- 計算復雜度不高
- 輸出結果易于理解
- 對中間值缺失不敏感
- 可以處理不相關特偵
缺點
- 可能產生過度匹配問題