批評不僅能讓人進步，也能讓大模型的能力提升。

OpenAI就用這個思路造了個“找茬模型”CriticGPT。非常巧合的是，就在CriticGPT放出的前幾天，北大聯合千問等團隊以類似的思路設計出了“數學專用版”CriticGPT。

在無需訓練的設置下，驗證器能夠在推理時輔助模型在GSM8K上的準確率從86.6%提升到88.2%。

在GSM8K數據集上，它可以讓模型的準確率從86.6%提升到88.2%。

CriticGPT的核心思路是在代碼中故意設置bug并進行詳細標注，然后用得到的數據訓練出會debug的模型。

北大團隊發現，這種方法不僅在代碼當中有用，也能幫助語言模型解決數學問題。

于是團隊利用相似的思路，把代碼換成數學問題，推出了“數學版CriticGPT”——Math-Minos。

用GPT4逐步提出修正意見

在數學推理領域，驗證解決方案的正確性，是確保推理質量的關鍵步驟。

然而，現有的數學驗證器大多依賴于二元分類標簽進行訓練，這種方式在提供正確或錯誤原因的解釋上存在明顯不足，無法給驗證器提供足夠充分的監督信號來訓練。

Math-Minos則克服了這一局限，提供了更深入的解釋，極大地豐富了驗證器的訓練信息。

它引入了逐步的自然語言反饋作為理由標簽，不僅指出了解決方案的正誤，還能逐步分析出錯誤的原因。

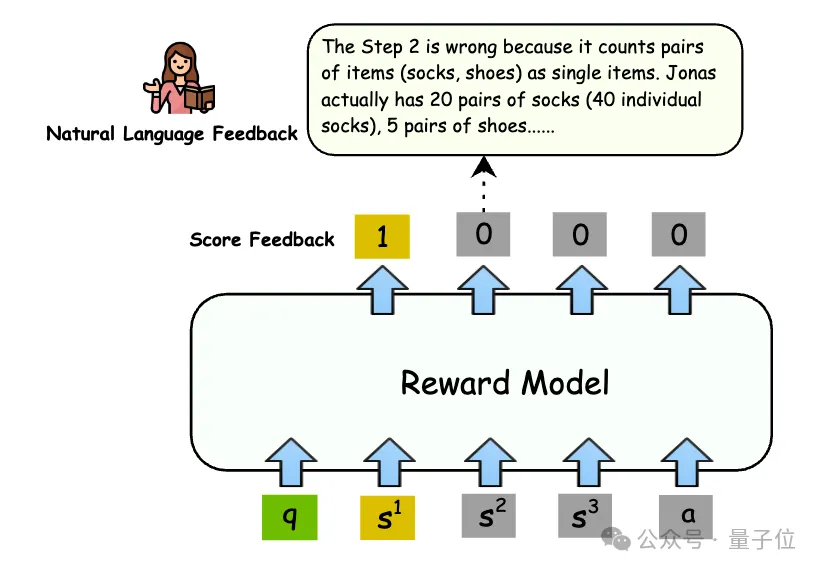
在自然語言反饋的獲取上，研究團隊一開始使用GPT-4生成訓練數據，但通過實驗發現，即使是GPT-4，在逐步評價數學推理任務時也會出現一定比例的錯誤。

為了一定程度避免這個問題，研究人員通過在提示中引入步驟級別的二元分類標簽，簡化了GPT-4的任務，使得GPT-4能夠更準確地生成評估。

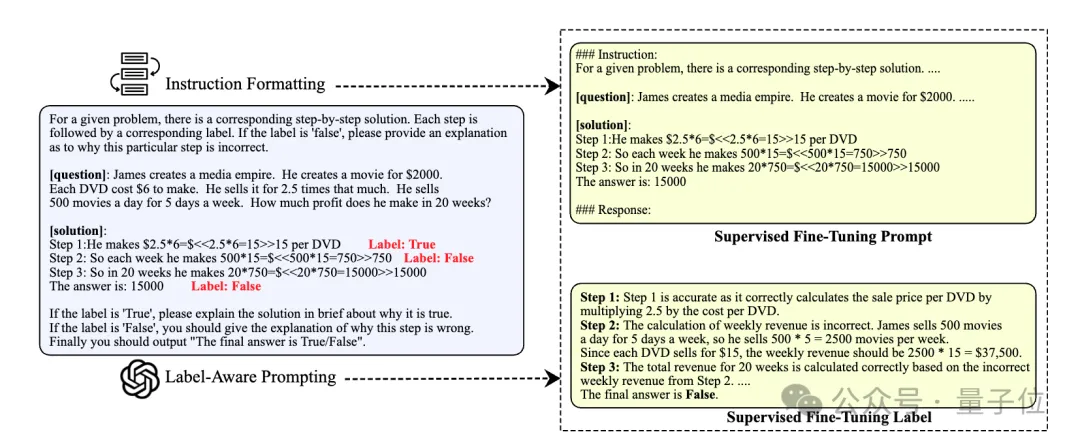
 首先，通過監督式微調，使用自然語言反饋作為訓練數據，有效提升了模型的評估能力。

其次，通過標準的ORM（Outcome Reward Model，輸出獎勵模型）和PRM（Process Reward Model，過程獎勵模型）訓練，實現了高效的推理，這種做法有兩個好處。

一是通過兩階段訓練，可以將二分類數據和監督微調數據解耦。

由于監督信號的稀疏性，訓練二分類的數據往往遠多于監督微調的數據，而研究發現，僅需要少量的監督微調數據，就可以很大程度提升模型的評估能力。

另一方面，在驗證器進行驗證時，不需要顯示地生成自然語言反饋，讓推理過程更高效。

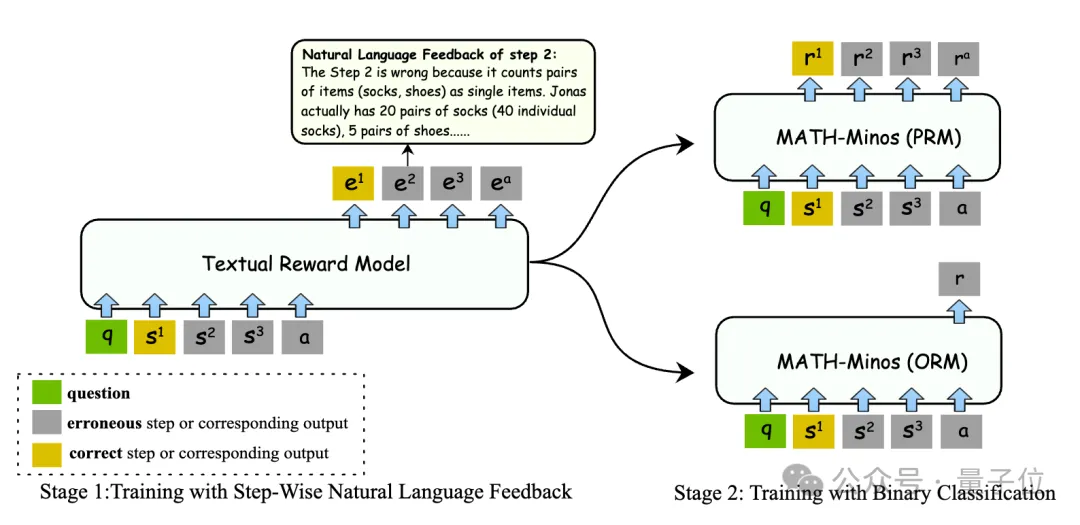
ORM任務表現明顯提升

總得來看，研究人員在訓練階段添加了30K的自然語言反饋數據，為Mistral-7B驗證器帶來了數學能力的提升，在Best-of-256的實驗設置下：

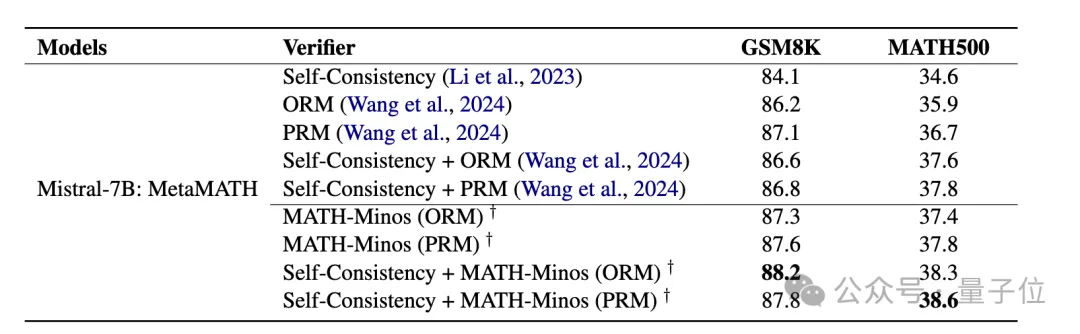
在ORM的設置下，MATH-Minos將Mistral-7B的準確率在GSM8K數據集從86.2%提升到87.3%，在MATH數據集從35.9%提升到37.4%。

在PRM的設置下，MATH-Minos將Mistral-7B的準確率在GSM8K數據集從87.1%提升到87.6%，在MATH數據集從36.7%提升到37.8%。

在與Self-Consistency結合的設置下，MATH-Minos將Mistral-7B的準確率在GSM8K數據集從87.1%提升到88.2%，在MATH數據集從37.8%提升到38.6%。

在ORM和PRM任務設置中，Math-Minos均展現出了優越的性能，特別是在ORM設置中，其改進更為顯著。

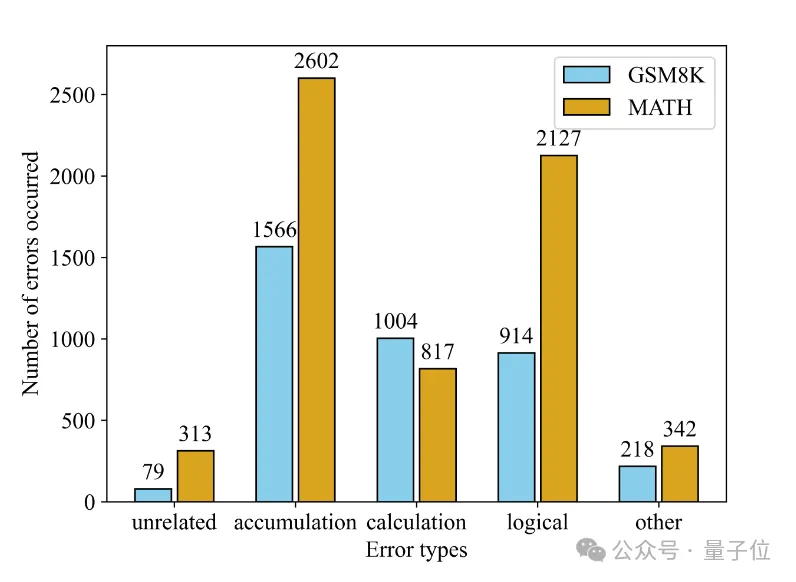
另外，研究團隊還對生成器在步驟級別產生的錯誤進行了深入分析，將其歸類為五種類型——無關錯誤、累積錯誤、計算錯誤、邏輯錯誤和其他錯誤。

分析結果表明，在多步驟推理中，步驟錯誤的可能原因有很多種，而且模型在這些錯誤類型中都有可能出錯，這進一步強調了引入自然語言反饋來指導模型學習的重要性。

實驗發現，在兩個數據集上，累積錯誤（即一個步驟的錯誤很可能直接導致所有后續步驟的錯誤）在所有錯誤類型中占到的比例最高。

不同數據集上的錯誤分布也有不同的特點，在相對簡單的GSM8K上，計算錯誤更多；在更困難的MATH數據集上，邏輯錯誤更多。

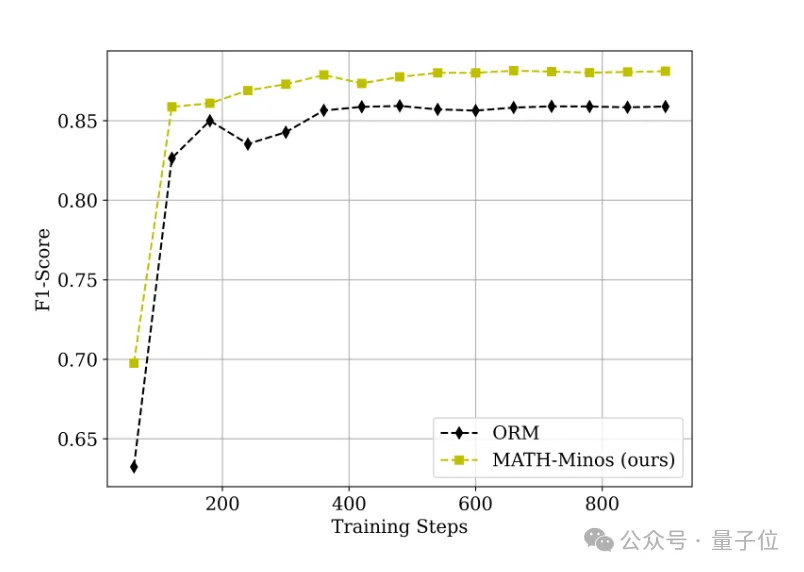
通過構建元評估集，研究團隊評估了驗證器在沒有生成器影響下，準確判斷最終答案的能力。

結果顯示，Math-Minos在訓練過程中的元評估一致優于傳統的ORM，并且展現出更快的收斂速度和更精準的判斷能力。

同時實驗結果也表明，Math-Minos具有很強的Scale Up的潛力。

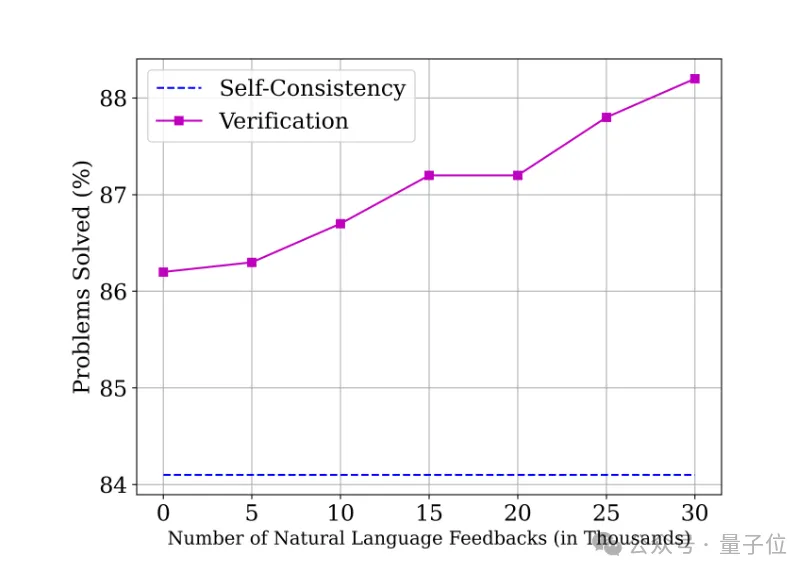
總之，Math-Minos的開發不僅提升了數學驗證器的性能，更為自然語言處理領域提供了一種新的訓練范式。

研究團隊希望這項工作能夠啟發未來研究，探索自然語言反饋與分類式驗證器的潛在整合，推動大型語言模型在復雜推理任務上的能力。

論文地址：https://arxiv.org/abs/2406.14024
GitHub：https://github.com/KbsdJames/MATH-Minos