僅微調0.02%參數,性能接近全量微調!上交大推出高效微調統一新范式
Scaling Laws當道,但隨著大模型應用的發展,基礎模型不斷擴大的參數也成了令開發者們頭疼的問題。
為了減輕訓練負擔,Adapter、Prompt-Tuning以及LoRA等高效微調(Parameter Efficient Fine-Tuning, PEFT)算法越來越受到大家伙的青睞。
那么,問題來了——
盡管近年來高效微調領域發展迅速,涌現了多種方法,但不同PEFT方法背后的數學基礎幾乎沒有得到深入研究。
此外,不同PEFT方法之間的性能差異及其原因尚未系統地探討。這種理論深度的缺乏限制了研究者對這些方法潛在優勢和局限性的理解,阻礙了它們在實際應用中的優化和創新。
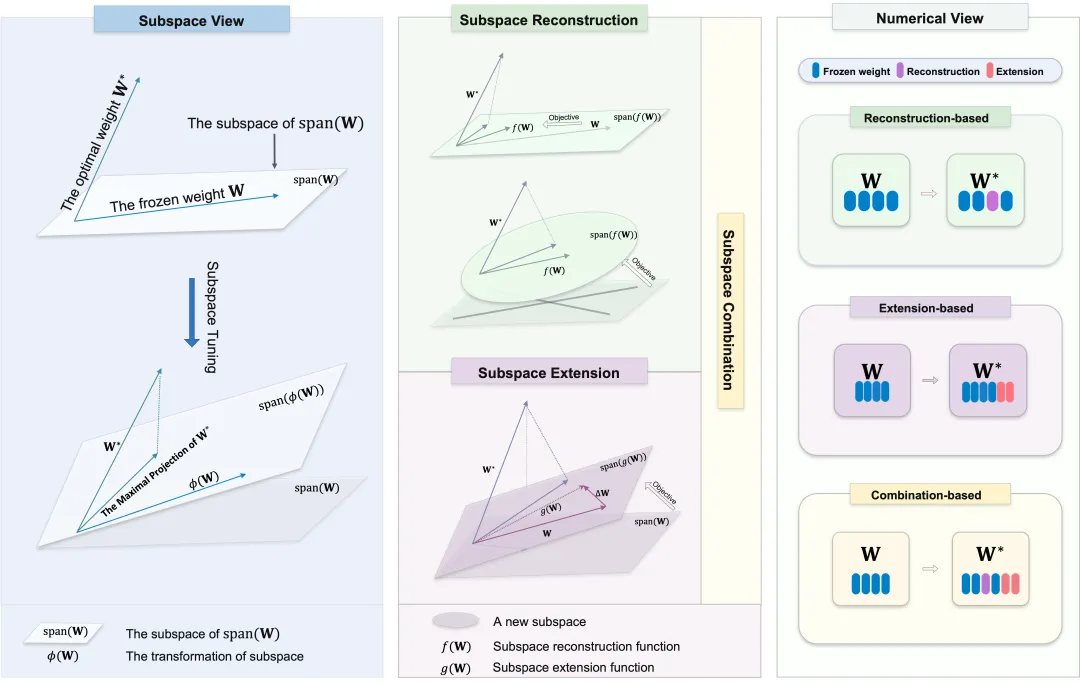
為了解決這一問題,來自上海交通大學的研究者們在對各種PEFT方法進行全面數學分析后,提出了一種新的框架——子空間微調,旨在將所有已知的PEFT方法統一在一個理論下,

具體來說,子空間微調方法主要集中于調整原始參數的子空間,涉及子空間的重構和擴展。研究者深入探討了不同方法如何操作子空間,并從分解理論的角度闡明了每種方法的數學原理。此外,研究者分析了為什么這些方法會導致性能差異,提供了理解不同PEFT策略內在動態的全面理論基礎。
他們基于此提出了兩種新的PEFT方法,新方法在僅微調0.02%參數的情況下,性能接近于全面微調。
研究者還介紹了一個有效的框架,在不引入額外訓練參數的情況下,提升了LoRA等方法的性能。通過在三種不同模型上測試超過十種方法,廣泛的實驗驗證了其理論的穩健性,同時展示了提出的方法和框架的有效性。
來看論文細節。
子空間微調理論
考慮任何給定主干網絡層的凍結權重矩陣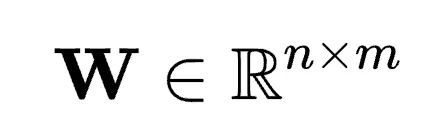 ,其中n≤m,并用權重矩陣
,其中n≤m,并用權重矩陣 的性能
的性能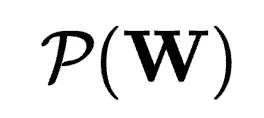 來量化模型的性能,值越高表示性能越好。
來量化模型的性能,值越高表示性能越好。
假設存在最優權重矩陣 ,且
,且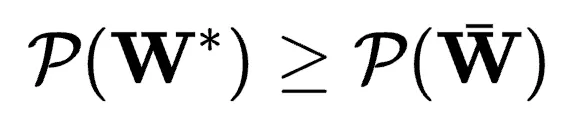 對所有
對所有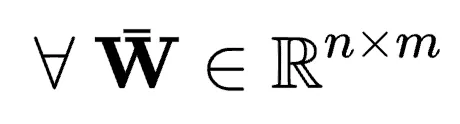 成立。PEFT的目標公式化為:
成立。PEFT的目標公式化為:
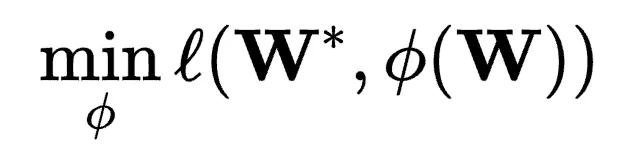
其中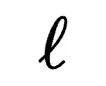 衡量兩個矩陣之間的差異。函數
衡量兩個矩陣之間的差異。函數 被視為增量調優,表示對矩陣
被視為增量調優,表示對矩陣 的每個元素的修改,但這種表征過于籠統。
的每個元素的修改,但這種表征過于籠統。
從分解理論的角度看,調整矩陣涉及修改其對應的子空間,因此,所有PEFT方法可視為子空間微調。
如此,優化的目標是找到 在
在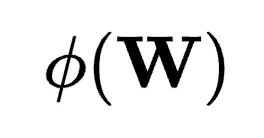 基所生成的子空間內的最大投影,然后將
基所生成的子空間內的最大投影,然后將 與其對齊。
與其對齊。
有兩種方法實現這一目標:通過調整 來逼近
來逼近 ,或操作
,或操作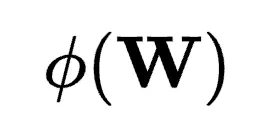 的子空間以接近或包含
的子空間以接近或包含 。
。
研究者將函數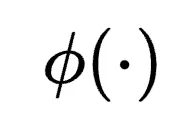 分配給兩個主要角色:直接重構對應
分配給兩個主要角色:直接重構對應 的子空間,以更好地對齊
的子空間,以更好地對齊 ,或引入一個新子空間并與原始子空間結合。這些過程數學表示為:
,或引入一個新子空間并與原始子空間結合。這些過程數學表示為:
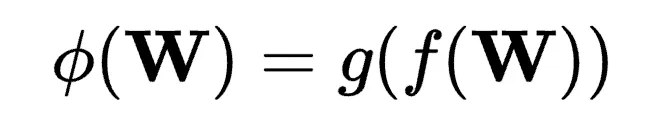
其中,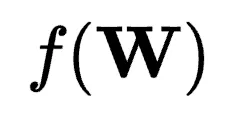 概括了
概括了 的子空間重構過程,
的子空間重構過程,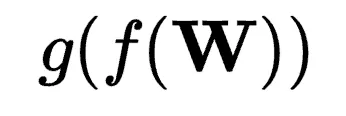 描述了子空間的聯合。研究者將這些操作分別稱為“子空間重構”和“子空間擴展”,并將現有方法分類為三類:
描述了子空間的聯合。研究者將這些操作分別稱為“子空間重構”和“子空間擴展”,并將現有方法分類為三類:
- 基于子空間重構的方法,將復雜空間分解為易理解的子空間,并調整這些派生子空間的基
- 基于子空間擴展的方法,引入一個新子空間,在新子空間和原始權重矩陣
 對應的子空間基所生成的空間內找到最優權重
對應的子空間基所生成的空間內找到最優權重 的最大投影;
的最大投影; - 基于子空間組合的方法,同時采用上述子空間調整。
子空間重構
基于先前概述的框架,子空間重構方法首先將 的空間分割為可解釋的子空間,然后細化這些子空間以提高模型效率。許多PEFT策略集中于直接重構與原始權重矩陣相關的子空間,著名例子包括SAM-PARSER、Diff Pruning、(IA)3、BitFit、Prefix-tuning和Prompt-tuning等。
的空間分割為可解釋的子空間,然后細化這些子空間以提高模型效率。許多PEFT策略集中于直接重構與原始權重矩陣相關的子空間,著名例子包括SAM-PARSER、Diff Pruning、(IA)3、BitFit、Prefix-tuning和Prompt-tuning等。
研究者從奇異值分解(SVD)開始探索,原始權重矩陣 被分解為正交子空間,涵蓋了原始矩陣空間的全部。分解表示為
被分解為正交子空間,涵蓋了原始矩陣空間的全部。分解表示為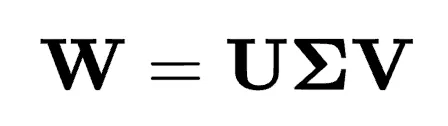 ,這種分解將
,這種分解將 分成左奇異向量
分成左奇異向量 (
( 列空間的正交基)、奇異值
列空間的正交基)、奇異值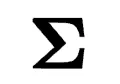 (調整維度和縮放)和右奇異向量
(調整維度和縮放)和右奇異向量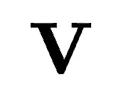 (
( 行空間的正交基)。通過調整分解獲得的子空間,可以重構原始空間,分為三種模式:
行空間的正交基)。通過調整分解獲得的子空間,可以重構原始空間,分為三種模式:
- 奇異值調整:調整
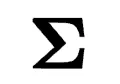 中的奇異值,修改每個主成分的權重,而不影響子空間方向。
中的奇異值,修改每個主成分的權重,而不影響子空間方向。 - 簡單奇異向量調整:通過縮放生成的子空間來調整
 和
和 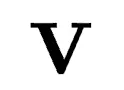 中的奇異向量,保留方向特性,同時調整幅度。
中的奇異向量,保留方向特性,同時調整幅度。 - 復雜奇異向量調整:對奇異向量進行更復雜的變換,重新定向或重塑子空間,全面調整矩陣結構。
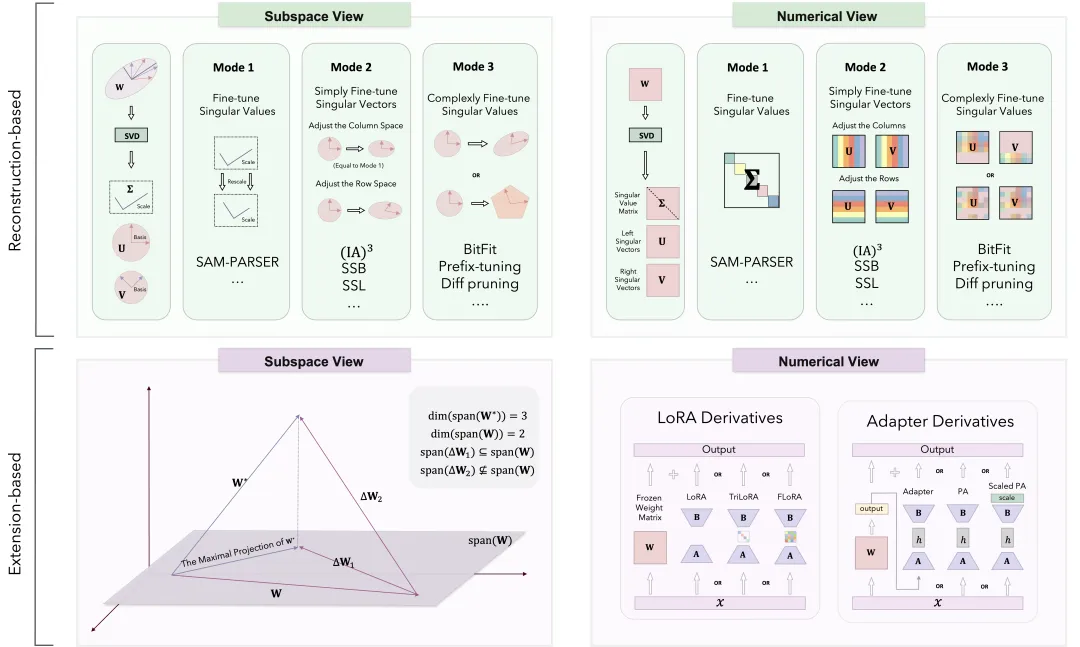
基于這一理論,研究者提出了兩種新的微調方法:SSL(Scaling the Subspace of the Left singular vectors)和SSB(Scaling the Subspace of Both left and right singular vectors)。
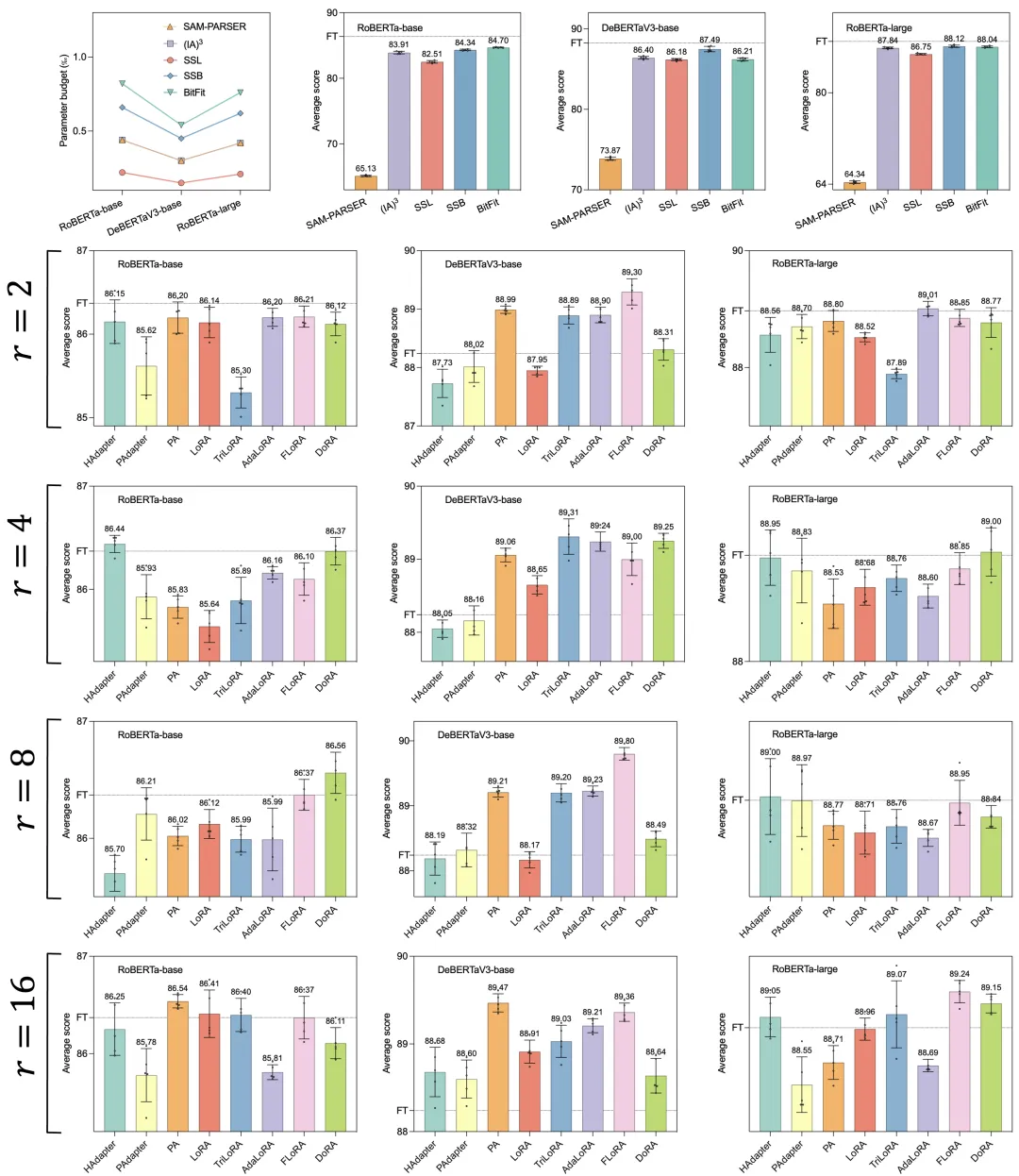
從下圖中可以看出,SSL最少只需要微調0.02%的參數,SSB最少只需要微調0.06%的參數,就能實現全量微調99%的性能。
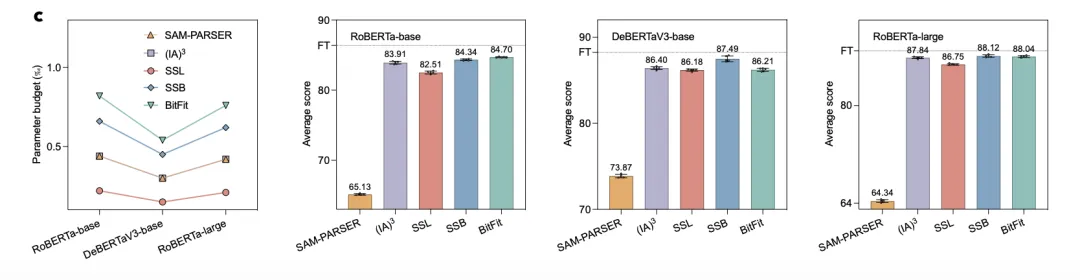
關于每種模式的具體操作、每種方法的具體內容、其背后的數學原理,以及研究者如何基于這一理論提出兩種新方法的詳細信息,請參閱原論文。
子空間擴展
基于擴展的方法引入新子空間,結合該新子空間和原始權重矩陣 的基生成擴展空間。
的基生成擴展空間。
這些方法旨在找到最優權重 在新空間內的最接近投影,通過引入額外的權重矩陣來擴大原始子空間的基以覆蓋更大維度區域。通常,這些方法的轉換函數定義為
在新空間內的最接近投影,通過引入額外的權重矩陣來擴大原始子空間的基以覆蓋更大維度區域。通常,這些方法的轉換函數定義為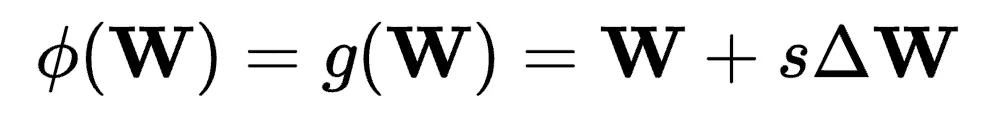 ,其中s代表縮放因子,
,其中s代表縮放因子,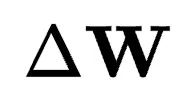 對應于新子空間,也稱為附加項。
對應于新子空間,也稱為附加項。
考慮權重矩陣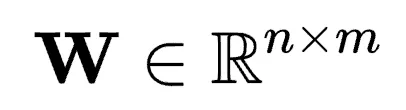 ,假設n≤m。理想情況下,有
,假設n≤m。理想情況下,有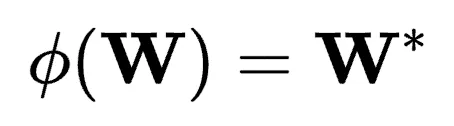 ,即
,即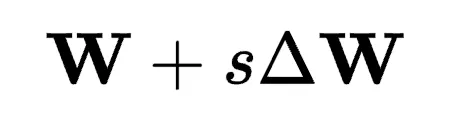 和
和 占據相同的行和列空間,使它們定位在同一超平面內。
占據相同的行和列空間,使它們定位在同一超平面內。
如果 的秩為n,其列空間的維度等于n,生成
的秩為n,其列空間的維度等于n,生成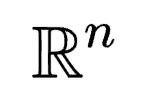 子空間。若
子空間。若 的秩小于n,它只能在
的秩小于n,它只能在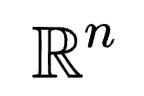 內生成一個子空間。假設
內生成一個子空間。假設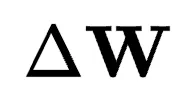 和
和 的列空間基可以生成整個
的列空間基可以生成整個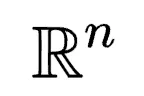 空間,在最優情況下,
空間,在最優情況下,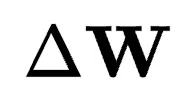 的列基向量應補充
的列基向量應補充 的列基,意味著
的列基,意味著 的列空間代表這些空間的直和。
的列空間代表這些空間的直和。
一些研究表明,最優權重 會放大原始權重矩陣中某些特定任務的方向,這些方向對于預訓練并不關鍵。此外,最優權重還會調整
會放大原始權重矩陣中某些特定任務的方向,這些方向對于預訓練并不關鍵。此外,最優權重還會調整 的主要方向。這些見解表明
的主要方向。這些見解表明 可能與
可能與 的子空間共享大量共同基。因此,
的子空間共享大量共同基。因此,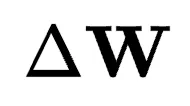 可能只需考慮
可能只需考慮 中缺少但
中缺少但 中存在的一小部分基,使
中存在的一小部分基,使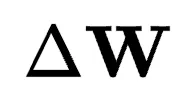 成為低秩矩陣。
成為低秩矩陣。
實證研究表明,預訓練模型的全參數微調通常可重新參數化為在低維子空間內優化,表明最優權重在這個受限的低秩子空間內變化。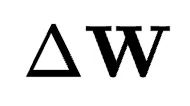 的低秩特性突出了基于擴展方法的參數效率基礎。
的低秩特性突出了基于擴展方法的參數效率基礎。
另一個關鍵方面是縮放因子s。基于擴展的方法目標是確定 在
在 和
和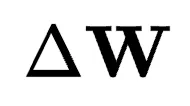 形成的超平面內的最大投影,確保
形成的超平面內的最大投影,確保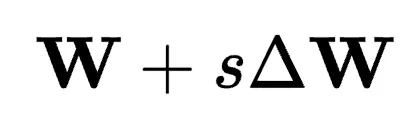 盡可能與
盡可能與 方向對齊。給定固定的
方向對齊。給定固定的 和
和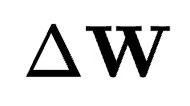 ,只有一個s值能使 \
,只有一個s值能使 \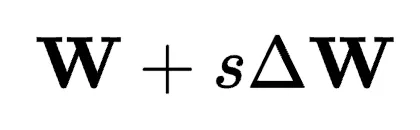 的方向與
的方向與 方向對齊,因此s值對性能的影響可能非常顯著。
方向對齊,因此s值對性能的影響可能非常顯著。
在參數高效微調中,有兩大系列基于擴展的方法。第一系列是LoRA衍生,包括LoRA、AdaLoRA、TriLoRA、FLoRA、VeRA等。第二系列是適配器衍生,包括Adapter(H),Adapter(P),Parallel Adapter等。
在此基礎之上,研究者提出了MPC框架,以進一步提升現有算法的性能。
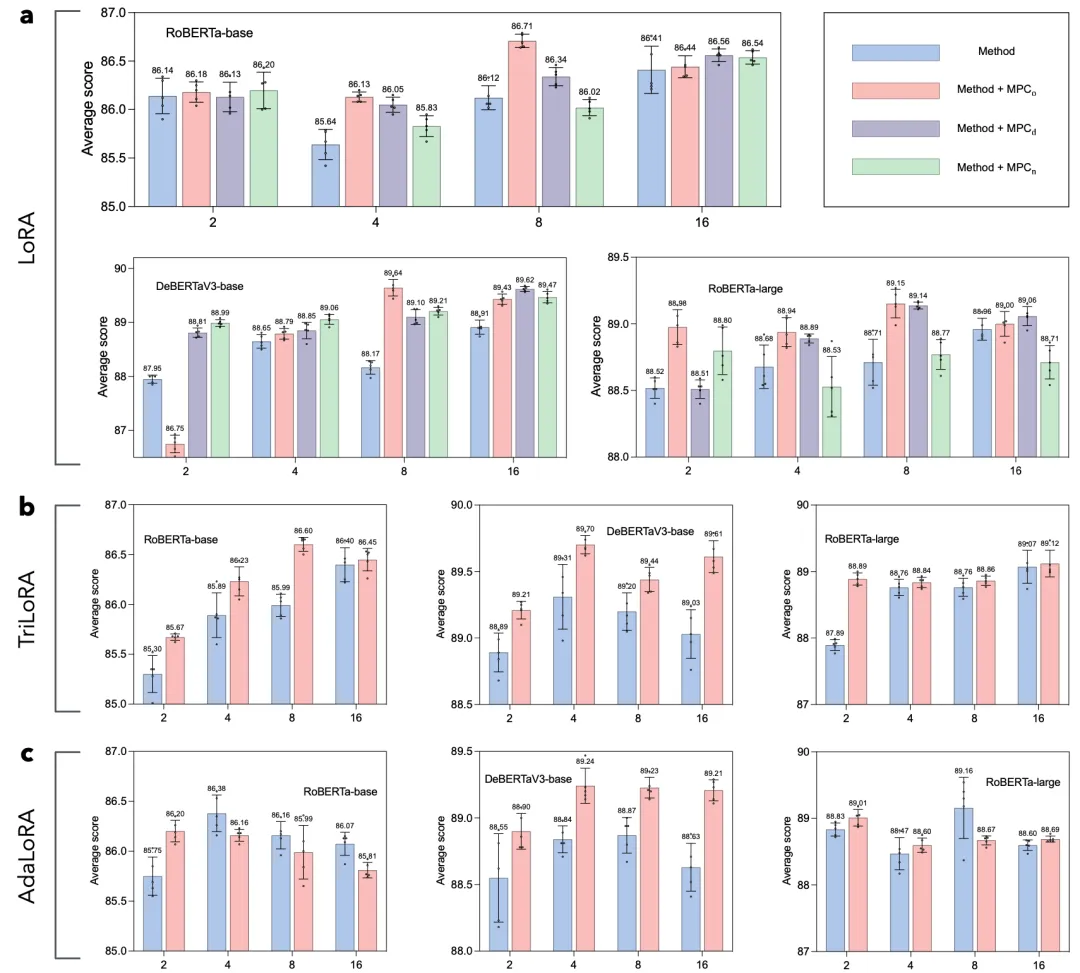
從下圖中可以看出,在不引入額外參數的情況下,MPC框架顯著增強了各種PEFT方法的性能。
另外,MPC可以幫助PEFT方法實現更穩定的訓練。與不使用MPC的方法相比,結合MPC的方法通常表現出更小的標準偏差。
關于這些方法的具體分析,LoRA和Adapter系列算法性能差異的原因,以及MPC框架的詳細設計思路,請參閱原論文。
子空間組合
基于組合的方法同時執行子空間重構和擴展,結合了這兩種方法的原理。
此外,對于某些方法,它們既可以分類為基于重構的方法,也可以分類為基于擴展的方法,研究者也將它們分類為基于組合的方法。研究者分析介紹幾種代表性的基于組合的方法,如DoRA,Spectral Adapter和SVDiff等。
關于這些方法的具體細節請參閱原論文。
論文:https://arxiv.org/pdf/2407.05417
代碼:https://github.com/Chongjie-Si/Subspace-Tuning











































