可解釋性終極追問,什么才是第一性解釋?20篇CCF-A+ICLR論文給你答案
本文作者為張俊鵬、任啟涵、張拳石,其中張俊鵬是張拳石老師的準入學博士生,任啟涵是張拳石老師的博士生。
本文首先簡單回顧了『等效交互可解釋性理論體系』(20 篇 CCF-A 及 ICLR 論文),并在此基礎上,嚴格推導并預測出神經網絡在訓練過程中其概念表征及其泛化性的動力學變化,即在某種程度上,我們可以解釋在訓練過程中神經網絡在任意時間點的泛化性及其內在根因。
一、前言
長期以來,我們團隊一直在思考可解釋性領域的一個終極問題,即什么才是解釋性領域的第一性原理?所謂第一性原理,目前沒有一個被廣泛接受的框架,世上本無路,我們需要逐漸去定義這樣一個路。我們需要在一個新的理論體系中,提出大量的公理性要求,得出一個可以從不同的角度全方位精確嚴謹解釋神經網絡內在機理的理論。一套理論系統能嚴謹解釋神經網絡的方方面面才叫 “第一性原理”。
如果你真的在嚴謹地做 “科學”,那么第一性原理一定不是想象中簡單,而是一個復雜的體系,需要研究照顧到深度學習中方方面面紛繁復雜的現象。當然,如果你主觀上不愿意或者不信一個理論需要足夠嚴謹,那么研究會變得簡單千萬倍。就像物理學的標準模型一定比牛頓定律復雜,取決于你希望走哪條路。
沿著這個方向,我們團隊獨立從頭構建了『等效交互可解釋性理論體系』,并基于此理論,從三個角度來解釋神經網絡的內在機理。
1. 語義解釋的理論基礎:數學證明神經網絡的決策邏輯是否可以被少量符號化邏輯所充分覆蓋(充分解釋)。『證明神經網絡的決策邏輯是否可以被有限符號化邏輯解釋清楚』這一命題是解釋神經網絡的根本命題。如果此命題被證偽,則從根本上講,神經網絡的可解釋性將是無望的,所有的解釋性算法只能提供近似的解讀,而無法精確地覆蓋所有的決策邏輯。幸運的是,我們找到了在大部分應用中神經網絡都可以滿足的面向遮擋魯棒性的三個常見的條件,并且數學證明了滿足這三個條件的神經網絡的決策邏輯可以被寫成符號化的交互概念。
參見 https://zhuanlan.zhihu.com/p/693747946
2. 尋找性能指標背后的可證明、可驗證的根因:將神經網絡泛化性和魯棒性等終極性能指標的根因拆分具體少數細節邏輯。對神經網絡性能(魯棒性、泛化性)的解釋是神經網絡可解釋性領域的另一個重大問題。然而,目前人們普遍認為神經網絡性能是對神經網絡整體的描述,而神經網絡無法像人類一樣將自己的分類判斷拆解成具象化的、少量的決策邏輯。在這方面,我們給出了不一樣的觀點 —— 將性能指標與具象化的交互之間建立起數學關系。我們證明了 1. 等效交互的復雜度可以直接決定神經網絡的對抗魯棒性 / 遷移性,2. 交互的復雜度決定了神經網絡的表征能力,3. 并解釋神經網絡的泛化能力 [1],和 4. 解釋神經網絡的表征瓶頸。
- 參見1:https://zhuanlan.zhihu.com/p/369883667
- 參見2:https://zhuanlan.zhihu.com/p/361686461
- 參見3:https://zhuanlan.zhihu.com/p/704760363
- 參見4:https://zhuanlan.zhihu.com/p/468569001
3. 統一工程性深度學習算法。由于缺少基礎理論的支撐,目前深度學習算法大都是經驗性的、工程性的。可解釋性領域的第一性原理應該可以承擔起將前人的大量工程性經驗總結為科學規律的任務。在等效交互可解釋性理論體系下,我們團隊既證明了 14 種不同的輸入重要性歸因算法的計算本質在數學上都可以統一寫成對交互作用的再分配形式。此外,我們還統一了 12 種提升對抗遷移性的算法,證明了所有提升對抗遷移性算法的一個公共機理是降低對抗擾動之間的交互效用,實現了對神經網絡可解釋性方向大部分工程性算法的理論凝練。
- 參見1:https://zhuanlan.zhihu.com/p/610774894
- 參見2:https://zhuanlan.zhihu.com/p/546433296
在等效交互可解釋性理論體系下,我們的團隊在之前的研究中已經成功發表了 20 篇 CCF-A 類和機器學習頂級會議 ICLR 論文,我們已經從理論和實驗上充分解答了上述問題。
二、本文研究概述
沿著上述理論框架,在這篇知乎文章中,我們希望精確解釋出神經網絡訓練過程中泛化性的變化規律,具體地涉及兩篇論文。
- 1.Junpeng Zhang, Qing Li, Liang Lin, Quanshi Zhang,“Two-Phase Dynamics of Interactions Explains the Starting Point of a DNN Learning Over-Fitted Features”,in arXiv: 2405.10262
- 2.Qihan Ren, Yang Xu, Junpeng Zhang, Yue Xin, Dongrui Liu, Quanshi Zhang,“Towards the Dynamics of a DNN Learning Symbolic Interactions” in arXiv:2407.19198

圖 1:兩階段現象的示意圖。在第一階段,神經網絡逐漸消除中高階交互,學習低階交互;在第二階段,神經網絡逐漸建模階數不斷增大的交互。當神經網絡訓練過程中測試損失和訓練損失之間的 loss gap 開始增大時,神經網絡恰好也進入訓練的第二階段。
我們希望在等效交互框架里提出新的理論,精確預測出神經網絡每一個時間點上神經網絡所學到的交互概念的數量、復雜度,以及泛化性變化的動力學規律(如圖 1 所示)。具體地,我們希望證明出兩方面結論。
第一,基于前人的證明(一個神經網絡的決策邏輯可以被嚴格解構表示為幾十個交互概念效用的和的形式),進一步嚴格推導出在整個訓練過程中,神經網絡所建模的交互效用的變化動力學過程 —— 即理論需精確預測出在不同訓練階段,神經網絡所建模的交互概念的分布的變化 —— 推導出哪些交互會在哪個時間點上被學習到。
第二,尋找充分的證據,證明所推導的交互復雜度的變化規律客觀反映出神經網絡在全訓練周期中泛化性變化的規律。
綜上兩點,我們希望具體徹底解釋清楚神經網絡的泛化性變化的內在根因。
與前人的關系:當然大家可能第一反應想到神經正切核(NTK)[2],但是神經正切核只是把參數的變化曲線解了出來,而沒辦法進一步深入到決策邏輯層面進行解釋,沒有將神經網絡建模的概念表征與其泛化性的關系建立起來,對泛化性的分析依然停留在特征空間分析的層面,而沒有在【符號化概念邏輯】與【泛化性】之間建立起嚴格的關系。
三、兩大研究背景
誤會 1:神經網絡的第一性表征是『等效交互』,而不是神經網絡的參數和結構。單純從結構層面分析神經網絡是人們對神經網絡泛化根本表征的誤解。目前大部分神經網絡泛化性研究主要著眼于神經網絡的結構、特征、以及數據。人們認為不同的神經網絡結構就自然對應不同的函數,并自然展現出不同的性能。
但是,事實上,如圖 2 所示,結構的區別只是神經網絡表征的表面形式。除去有明顯缺陷的對性能有明顯影響的神經網絡,所有其他可以實現 SOTA 性能的具有不同結構的神經網絡往往都建模了相似的等效交互表征,即不同結構的高性能神經網絡在等效交互表征上往往都是殊途同歸的 [3, 4]。雖然神經網絡其中層特征內部是復雜的混亂的,雖然不同神經網絡所建模的特征向量大相徑庭,雖然神經網絡中單個神經元往往建模了相對比較混亂的語義(不是嚴格清晰的語義),但是神經網絡作為一個整體,我們從理論上證明神經網絡的所建模的交互關系是稀疏的符號化的(而不是特征的稀疏性,具體見 “四、交互的定義” 章節),而且面向相同任務的完全不同的神經網絡往往建模了相似的交互關系。
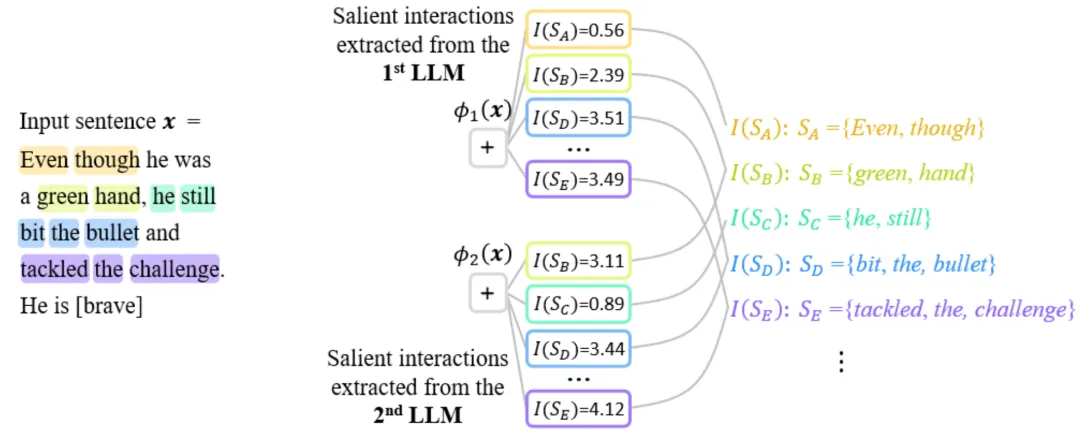
圖 2:不同結構的神經網絡所建模的等效交互往往是殊途同歸的。對于一個相同的輸入句子,面向兩個相同任務的兩個完全不同的神經網絡建模往往相似的交互。
由于不同神經網絡的參數和訓練樣本不一樣,兩個神經網絡中沒有任何一個神經元在表征上具有嚴格的一一對應關系,且每一個神經元往往建模著不同語義的混合模式。相比之下,正如上段分析,神經網絡所建模的交互表征實際上是不同神經網絡表征中的不變量。因此,我們有理由認為神經網絡根本表征是等效交互,而不是其載體(參數和訓練樣本),符號化交互表征可能代表了知識表征的第一性原理(被交互的稀疏性定理、無限擬合性定理、以及殊途同歸現象所保證,見 “四、交互的定義” 章節,具體詳細研究見下面知乎文章。
參見:https://zhuanlan.zhihu.com/p/633531725
誤會 2:神經網絡的泛化性問題是一個混合模型問題,而不是一個高維空間的向量。如圖 3 所示,傳統的泛化性分析總是假設單個樣本整體是高維空間的一個點,實際上神經網絡對單個樣本的表征是 mixture model 的形式 —— 實際上通過大量不同的交互來表達。我們發現簡單交互的泛化能力比復雜交互的泛化能力更強,所以不再適合用一個簡單標量來籠統表示整個神經網絡在不同樣本上的泛化能力。相反,同一個神經網絡在不同的樣本上建模了不同復雜度的交互關系,而不同復雜度的交互往往對應著不同泛化能力。通常情況下,神經網絡建模的高階(復雜)的交互往往難以泛化到測試樣本上(測試樣本上不會觸發相同的交互),代表過擬合表征,而神經網絡建模的低階(簡單)交互往往代表泛化性較強的表征,具體詳細研究見 [1]。
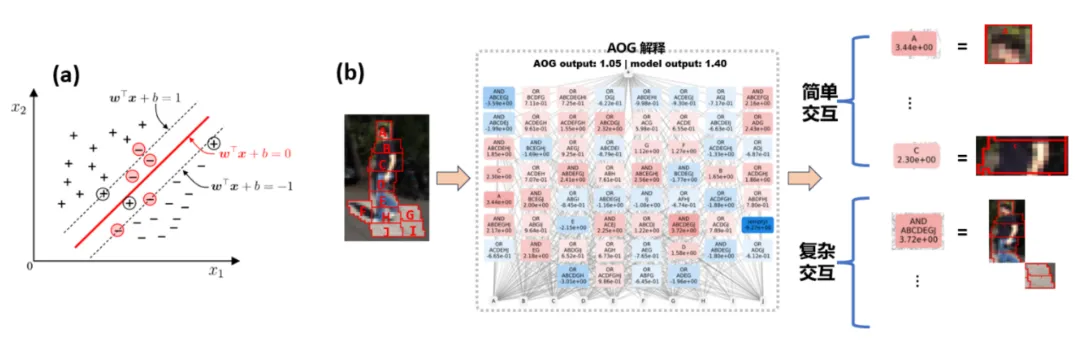
圖 3:(a)傳統的泛化性分析總是假設單個樣本整體是高維空間的一個點。(b)實際上神經網絡對單個樣本的表征是 mixture model 的形式,神經網絡在單個樣本會建模簡單交互(可泛化的交互)和復雜交互(不可泛化的交互)。
四、交互的定義
讓我們考慮一個深度神經網絡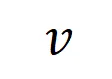 和一個輸入樣本
和一個輸入樣本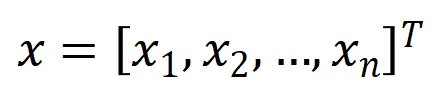 ,它包含
,它包含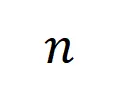 個輸入變量,我們用集合
個輸入變量,我們用集合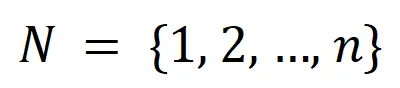 表示這些輸入變量的全集。令
表示這些輸入變量的全集。令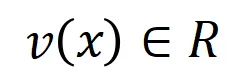 表示 DNN 在樣本
表示 DNN 在樣本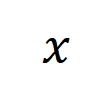 上的一個標量輸出。對于一個面向分類任務的神經網絡,我們可以從不同角度來定義其標量輸出。例如,對于多類別分類問題,
上的一個標量輸出。對于一個面向分類任務的神經網絡,我們可以從不同角度來定義其標量輸出。例如,對于多類別分類問題,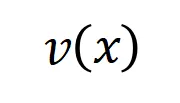 可以定義為
可以定義為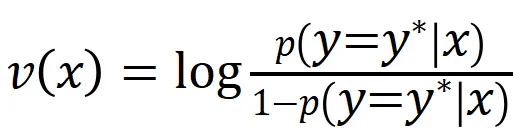 ,也可以定義為 softmax 層之前該樣本真實標簽所對應的標量輸出。這里,
,也可以定義為 softmax 層之前該樣本真實標簽所對應的標量輸出。這里,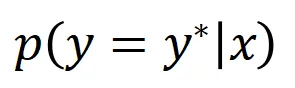 表示真實標簽的分類概率。這樣,針對每個子集
表示真實標簽的分類概率。這樣,針對每個子集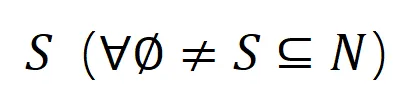 ,我們可以用下面公式來定義
,我們可以用下面公式來定義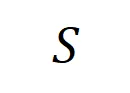 中所有輸入變量之間 “等效與交互” 和 “等效或交互”。
中所有輸入變量之間 “等效與交互” 和 “等效或交互”。
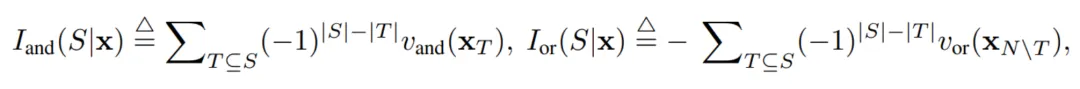
如圖 4(a)所示,我們可以這樣理解上述與或交互:我們可以認為與等效交互表示神經網絡所編碼的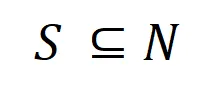 內輸入變量之間的 “與關系”。例如,給定一個輸入句子
內輸入變量之間的 “與關系”。例如,給定一個輸入句子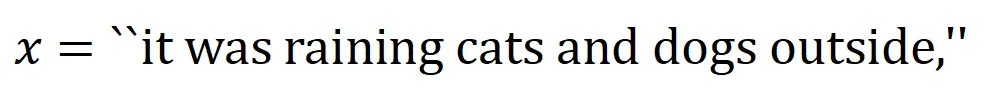 ,神經網絡可能會在
,神經網絡可能會在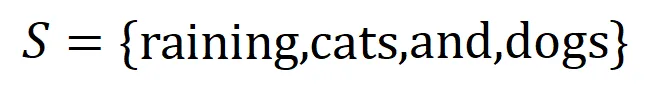 之間建模一個交互,使得
之間建模一個交互,使得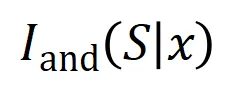 產生一個推動神經網絡輸出 “傾盆大雨” 的數值效用。如果
產生一個推動神經網絡輸出 “傾盆大雨” 的數值效用。如果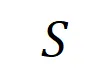 中的任何輸入變量被遮擋,則該數值效用將從神經網絡的輸出中移除。類似地,等效或交互
中的任何輸入變量被遮擋,則該數值效用將從神經網絡的輸出中移除。類似地,等效或交互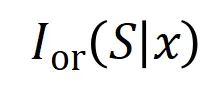 表示神經網絡所建模的
表示神經網絡所建模的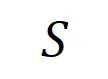 內輸入變量之間的 “或關系”。例如,給定一個輸入句子
內輸入變量之間的 “或關系”。例如,給定一個輸入句子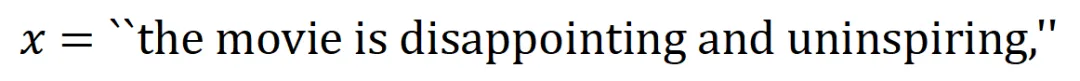 ,只要
,只要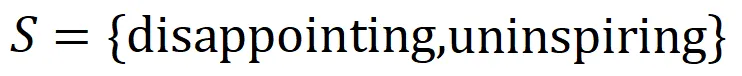 中的任意一個詞出現,就會推動神經網絡的輸出負面情感分類。
中的任意一個詞出現,就會推動神經網絡的輸出負面情感分類。
神經網絡所建模的等效交互滿足 “理想概念” 的三條公理性準則,即無限擬合性、稀疏性、樣本間遷移性。
- 無限擬合性:如圖 4,5 所示,對于任意遮擋樣本,神經網絡在樣本上的輸出可以用不同交互概念的效用之和來擬合。即,我們可以構造出一個基于交互的 logical model,無論我們如何遮擋輸入樣本,這個 logical model 依然可精確擬合模型在此輸入樣本在任意遮擋狀態下的輸出值。
- 稀疏性:面向分類任務的神經網絡往往只建模少量的顯著交互概念,而大部分交互概念都是數值效用都接近于 0 的噪聲。
- 樣本間遷移性:交互在不同樣本間是可遷移的,即神經網絡在(同一類別的)不同樣本上建模的顯著交互概念往往有很大的重合。
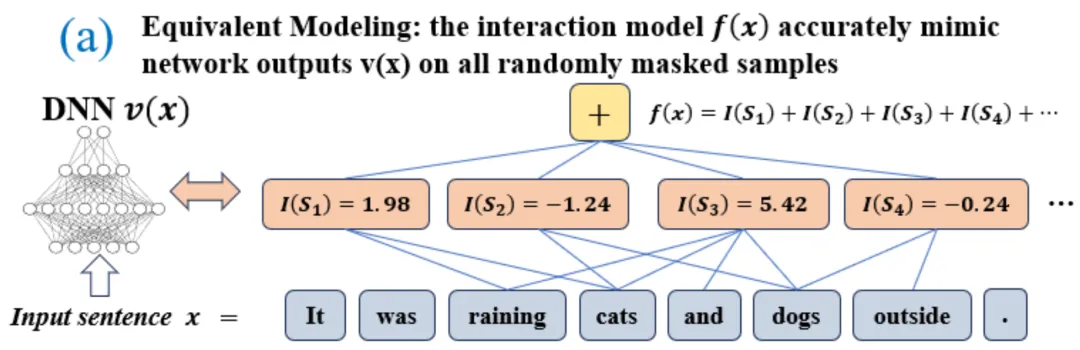
圖 4:神經網絡的復雜的推理邏輯可以被基于少量交互的邏輯模型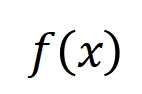 準確擬合。每個交互都是衡量神經網絡建模特定輸入變量集合
準確擬合。每個交互都是衡量神經網絡建模特定輸入變量集合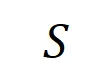 之間非線性關系的度量指標。當且僅當集合中變量同時出現時才會觸發與交互,并為輸出貢獻數值分數
之間非線性關系的度量指標。當且僅當集合中變量同時出現時才會觸發與交互,并為輸出貢獻數值分數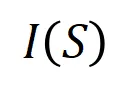 ,集合
,集合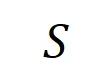 中任意變量出現時會觸發或交互。
中任意變量出現時會觸發或交互。
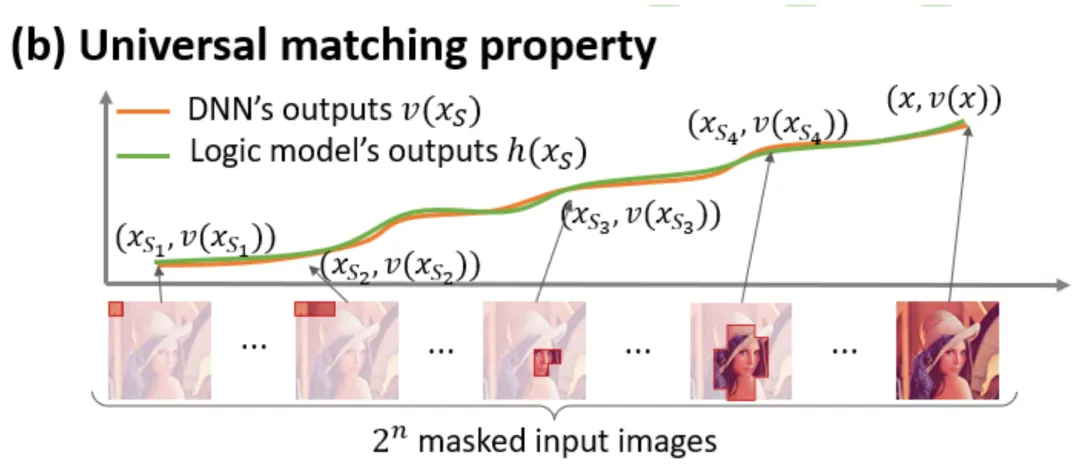
圖 5:神經網絡在任意的遮擋樣本上的輸出可以用不同交互概念的效用之和來擬合,即我們可以構造出一個基于交互的 logical model,無論我們如何遮擋輸入樣本,哪怕窮舉個輸入單元上種完全不同的遮擋方式,這個 logical model 依然可精確擬合模型在此輸入樣本在任意遮擋狀態下的輸出值。
五、新的發現與證明
5.1 發現神經網絡在訓練過程中交互變化的兩階段現象
在這篇知乎文章中,我們關注神經網絡解釋性領域的一個根本問題,即如何從一個解析分析的角度去嚴格預測出神經網絡在訓練過程中泛化能力的變化情況,并且精確的分析神經網絡從欠擬合到過擬合的整個動態變化過程及其背后的根本原因。
首先,我們將交互的階數(復雜度)定義為交互中的輸入變量的數量,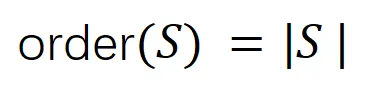 。我們團隊之前的工作發現神經網絡在某個特定樣本所建模的 “與或交互” 的復雜度直接決定了神經網絡在這個樣本的泛化能力 [1],即神經網絡建模的高階的(大量輸入單元之間的)“與或交互” 往往有較差的泛化能力,而低階的(少量輸入單元之間的)“與或交互” 具有較強的泛化能力。
。我們團隊之前的工作發現神經網絡在某個特定樣本所建模的 “與或交互” 的復雜度直接決定了神經網絡在這個樣本的泛化能力 [1],即神經網絡建模的高階的(大量輸入單元之間的)“與或交互” 往往有較差的泛化能力,而低階的(少量輸入單元之間的)“與或交互” 具有較強的泛化能力。
因此,本篇研究的第一步是去預測出神經網絡在訓練過程中不同時間點所建模的不同階 “與或交互” 的復雜度的一個解析解,即我們可以通過神經網絡在不同時間點所建模的不同階 “與或交互” 的分布去解釋神經網絡在不同階段的泛化能力。交互的泛化能力的定義與神經網絡整體泛化能力的定義請見 “5.2 神經網絡所建模交互的階數和其泛化能力的關系” 章節。
我們提出兩個指標來表示不同階(復雜度)的交互的強度的分布。具體來說,我們用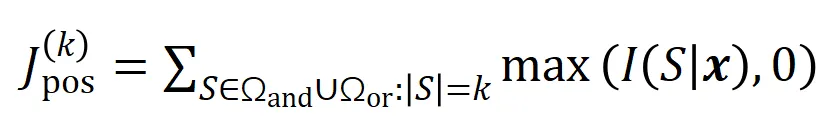 來衡量所有階正顯著交互的強度,用
來衡量所有階正顯著交互的強度,用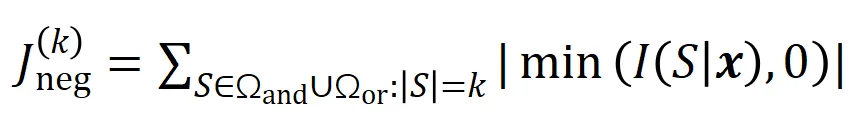 來衡量所有
來衡量所有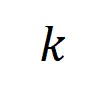 階負顯著交互的強度,其中
階負顯著交互的強度,其中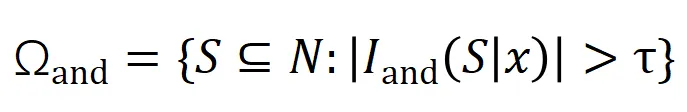 和
和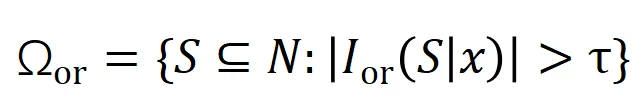 表示顯著交互的集合,
表示顯著交互的集合,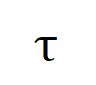 表示顯著交互的閾值。
表示顯著交互的閾值。
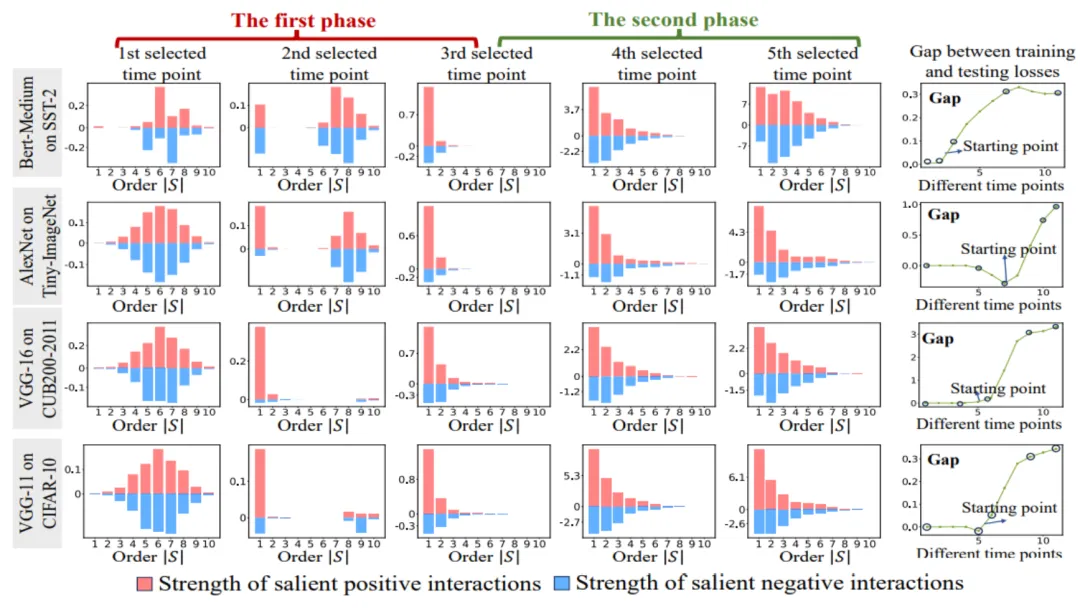
圖 6:從訓練不同輪次的神經網絡中提取的不同階交互強度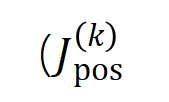 和
和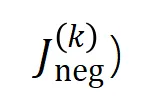 。在不同數據集上、不同任務上訓練的不同的神經網絡的訓練過程都存在兩階段現象。前兩個選定時間點屬于第一階段,而后兩個時間點屬于第二階段。恰恰在進入神經網絡訓練過程的第二階段不久,神經網絡的測試損失和訓練損失之間的 loss gap 開始顯著上升(見最后一列)。這表明神經網絡訓練的兩階段現象與模型 loss gap 的變化在時間上是 “對齊” 的。更多實驗結果請參見論文。
。在不同數據集上、不同任務上訓練的不同的神經網絡的訓練過程都存在兩階段現象。前兩個選定時間點屬于第一階段,而后兩個時間點屬于第二階段。恰恰在進入神經網絡訓練過程的第二階段不久,神經網絡的測試損失和訓練損失之間的 loss gap 開始顯著上升(見最后一列)。這表明神經網絡訓練的兩階段現象與模型 loss gap 的變化在時間上是 “對齊” 的。更多實驗結果請參見論文。
如圖 6 所示,神經網絡的兩階段現象具體表現為:
- 在神經訓練訓練之前,初始化的神經網絡主要編碼中階交互,很少編碼高階和低階交互,并且不同階交互的分布看起來呈現 “紡錘形”。假設具有隨機初始化參數的神經網絡建模的是純噪聲,我們在 “5.4 理論證明兩階段現象” 章節證明了具有隨機初始化參數的神經網絡建模的不同階的交互的分布呈現 “紡錘形”,即僅建模少量的低階和高階交互,大量建模中階交互。
- 在神經網絡訓練的第一階段,神經網絡編碼的高階和中階交互的強度逐漸減弱,而低階交互的強度逐漸增強。最終,高階和中階交互逐漸被消除,神經網絡只編碼低階交互。
- 在神經網絡訓練的第二階段,神經網絡在訓練過程中編碼的交互階數(復雜度)逐漸增加。在逐漸學習更高復雜度的交互的過程中,神經網絡過擬合的風險也在逐漸提高。
上述的兩階段現象廣泛存在于不同結構的神經網絡訓練于不同任務上的不同數據集的訓練過程中。我們在圖像數據集(CIFAR-10 數據集、MNIST 數據集、CUB200-2011 數據集(使用從圖片中裁剪出來的鳥類圖像)和 Tiny-ImageNet 數據集)上訓練了 VGG-11/13/16 和 AlexNet。我們在 SST-2 數據集上訓練了用于情感語義分類 Bert-Medium/Tiny 模型,我們在 ShapeNet 數據集中訓練 DGCNN 來分類的 3D 點云數據。上圖顯示了不同的神經網絡在不同訓練時期提取的不同階的顯著交互的分布。我們在這些神經網絡的訓練過程中都發現了兩階段現象,更多實驗結果及細節請參考論文。
5.2 神經網絡所建模交互的階數和其泛化能力的關系
我們團隊之前的工作已經發現了神經網絡所建模交互的階數和其泛化能力的關系,即高階交互比低階交互具有更差的泛化能力 [1]。某個具體交互的泛化性有清晰的定義 —— 如果一個交互同時在訓練樣本和測試樣本中頻繁的被神經網絡所建模,則這個交互具有較好的泛化能力。在本篇知乎文章中,介紹了兩個實驗來證明高階交互具有較差的泛化能力,低階交互具有較強的泛化能力。
實驗一:觀察在不同數據集上訓練的不同神經網絡所建模的交互的泛化性。這里我們用被測試集所觸發的交互的分布和被訓練集所觸發的交互的分布的 Jaccard 相似性來度量交互的泛化性。具體來說,給定一個包含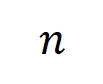 個輸入變量的輸入樣本
個輸入變量的輸入樣本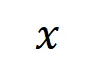 ,我們將從輸入樣本
,我們將從輸入樣本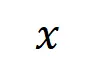 提取到的
提取到的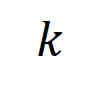 階交互向量化
階交互向量化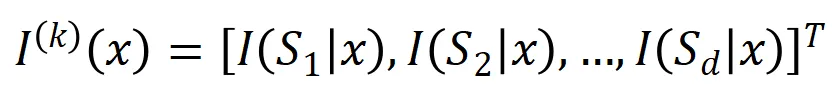 ,其中
,其中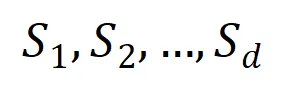 表示
表示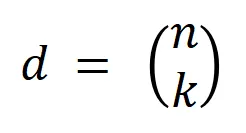 個
個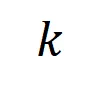 階交互。然后,我們計算分類任務中所有類別為
階交互。然后,我們計算分類任務中所有類別為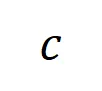 的樣本中提取到的
的樣本中提取到的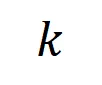 階的平均交互向量,表示為
階的平均交互向量,表示為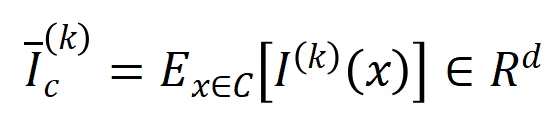 ,其中
,其中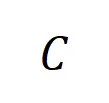 表示類別為
表示類別為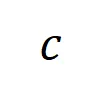 的樣本的集合。接下來,我們計算從訓練樣本中提取的階的平均交互向量
的樣本的集合。接下來,我們計算從訓練樣本中提取的階的平均交互向量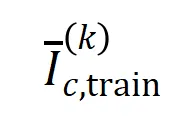 與從測試樣本中提取的
與從測試樣本中提取的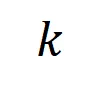 階的平均交互向量
階的平均交互向量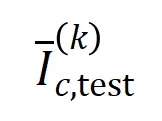 之間的 Jaccard 相似性,以衡量分類任務中類別為
之間的 Jaccard 相似性,以衡量分類任務中類別為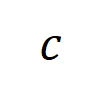 的樣本的
的樣本的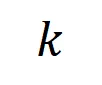 階交互的泛化能力,即:
階交互的泛化能力,即:
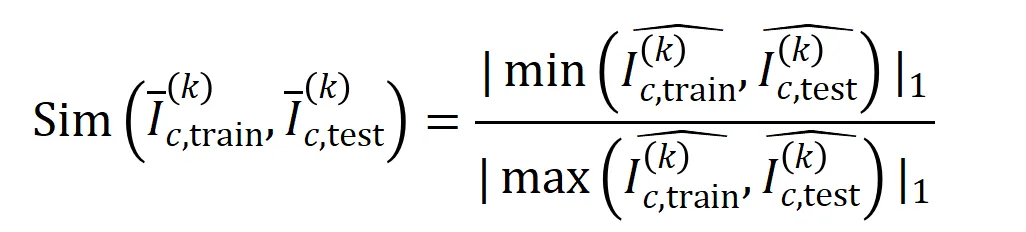
其中,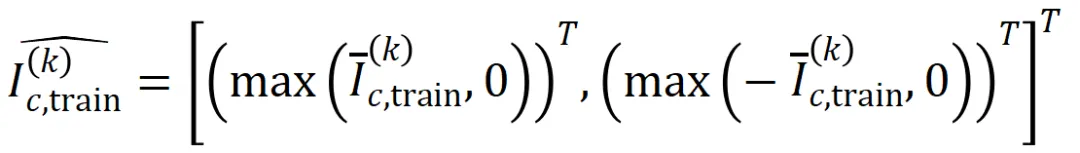 和
和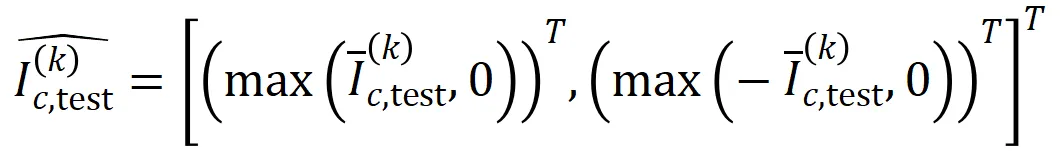 將兩個
將兩個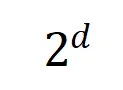 維交互向量投影到兩個
維交互向量投影到兩個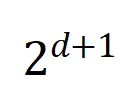 維的非負向量上,以便計算 Jaccard 相似性。對于某一階的交互,如果此階交互普遍展現出較大的 Jaccard 相似性,則表示這一階交互具有較強的泛化能力。
維的非負向量上,以便計算 Jaccard 相似性。對于某一階的交互,如果此階交互普遍展現出較大的 Jaccard 相似性,則表示這一階交互具有較強的泛化能力。
我們進行了實驗計算不同階交互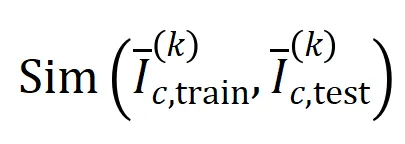 。我們測試了在 MNIST 數據集上訓練的 LeNet、在 CIFAR-10 數據集上訓練的 VGG-11、在 CUB200-2011 數據集上訓練的 VGG-13,以及在 Tiny-ImageNet 數據集上訓練的 AlexNet。為了減少計算成本,我們僅計算了前 10 個類別的 Jaccard 相似性的平均值
。我們測試了在 MNIST 數據集上訓練的 LeNet、在 CIFAR-10 數據集上訓練的 VGG-11、在 CUB200-2011 數據集上訓練的 VGG-13,以及在 Tiny-ImageNet 數據集上訓練的 AlexNet。為了減少計算成本,我們僅計算了前 10 個類別的 Jaccard 相似性的平均值 。如圖 7 所示,隨著交互階數的增加,交互的 Jaccard 相似性不斷下降。因此,這驗證了高階交互比低階交互具有更差的泛化能力。
。如圖 7 所示,隨著交互階數的增加,交互的 Jaccard 相似性不斷下降。因此,這驗證了高階交互比低階交互具有更差的泛化能力。
 圖 7:從訓練樣本和測試樣本中提取的交互之間的 Jaccard 相似性。低階交互具有相對較高 Jaccard 相似性表明低階交互具有較強的泛化能力。
圖 7:從訓練樣本和測試樣本中提取的交互之間的 Jaccard 相似性。低階交互具有相對較高 Jaccard 相似性表明低階交互具有較強的泛化能力。
實驗二:比較神經網絡在正常樣本和 OOD 樣本建模的交互的分布。我們比較了從正常樣本中提取的交互與從分布外 (OOD) 樣本中提取的交互,以檢查神經網絡在 OOD 樣本上是否建模更多的高階交互。我們將少量訓練樣本的分類標簽設置為錯誤標簽。這樣,數據集中的原始樣本可以視為正常樣本,而一些帶有錯誤標簽的樣本則對應于 OOD 樣本,這些 OOD 樣本可能會導致神經網絡的過擬合。我們在 MNIST 數據集和 CIFAR-10 數據集上分別訓練了 VGG-11 和 VGG-13。圖 8 比較了從正常樣本中提取的交互的分布和從 OOD 樣本中提取的交互的分布。我們發現,VGG-11 和 VGG-13 在分類 OOD 樣本時建模了更多復雜的交互(高階交互),而在分類正常樣本時則使用了較低階的交互。這驗證了高階交互的泛化能力通常弱于低階交互。
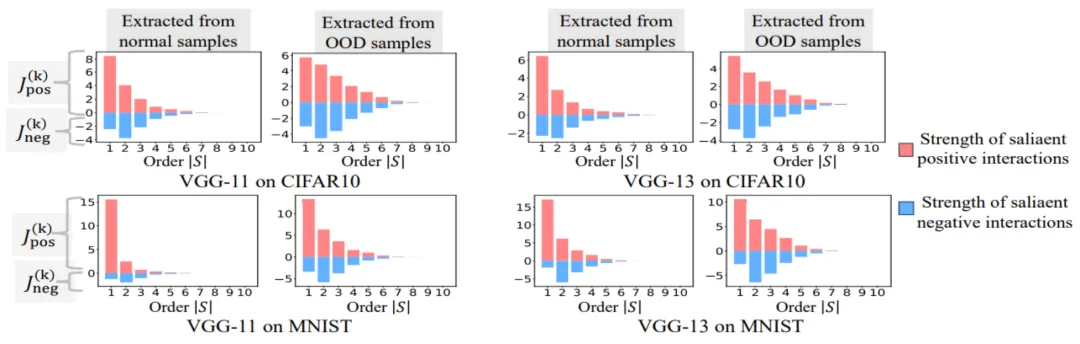
圖 8:比較從正常樣本中提取的交互與從分布外 (OOD) 樣本中提取的交互。神經網絡通常在 OOD 樣本上建模的更高階的交互。
5.3 兩階段現象和神經網絡訓練過程 loss gap 的變化相對齊
我們發現上述兩階段現象可以充分表示神經網絡泛化性動力學。一個很有趣的現象是神經網絡訓練過程中的兩階段現象和神經網絡在測試集和訓練集的 loss gap 的變化在時間上是對齊的。訓練損失和測試損失之間的 loss gap 是衡量模型過擬合程度的最廣泛使用的指標。圖 6 顯示了不同的神經網絡在訓練工程的測試損失和訓練損失之間的 loss gap 的曲線,還顯示了從不同訓練時期的神經網絡中提取的交互分布。我們發現當神經網絡訓練過程中測試損失和訓練損失之間的 loss gap 開始增大時,神經網絡恰好也進入訓練的第二階段。這表明神經網絡訓練的兩階段現象與模型 loss gap 的變化在時間上是 “對齊” 的。
我們可以這樣理解上述現象:在訓練過程開始前,初始化的神經網絡所建模的交互全部表示隨機噪聲,并且不同階交互的分布看起來像 “紡錘形”。在神經網絡訓練的第一階段,神經網絡逐漸消除中階和高階的交互,并學習最簡單的(最低階的)交互。然后,在神經網絡訓練的第二階段,神經網絡建模了階數逐漸增大的交互。由于我們在 “5.2 神經網絡所建模交互的階數和其泛化能力的關系” 章節中的兩個實驗驗證了高階交互通常比低階交互具有更差的泛化能力,因此我們可以認為在神經網絡訓練的第二階段,DNN 首先學習了泛化能力最強的交互,然后逐漸轉向更復雜但泛化能力較弱的交互。最終一些神經網絡逐漸過擬合,并編碼了大量中階和高階交互。
5.4 理論證明兩階段現象
理論證明神經網絡訓練過程的兩階段現象共分為三個部分,第一部分我們需要證明隨機初始化的神經網絡在訓練過程開始之前建模的交互的分布呈現 “紡錘形”,即很少建模高階和低階交互,主要建模中階交互。第二部分證明神經網絡在訓練的第二階段在建模階數逐漸增大的交互。第三部分證明神經網絡在訓練的第一階段逐漸消除中階和高階交互,學習最低價的交互。
1. 證明初始化神經網絡建模的 “紡錘形” 交互分布。
由于隨機初始化的隨網絡在訓練過程開始之前建模的都是噪聲,所以我們假設隨機初始化的神經網絡建模的交互的服從均值為 ,方差為
,方差為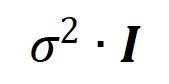 的正態分布。在上述假設下,我們能夠證明初始化的神經網絡建模的交互的強度和的分布呈現 “紡錘形”,即很少建模高階和低階交互,主要建模中階交互。
的正態分布。在上述假設下,我們能夠證明初始化的神經網絡建模的交互的強度和的分布呈現 “紡錘形”,即很少建模高階和低階交互,主要建模中階交互。

2. 證明神經網絡訓練的第二階段的交互變化動態過程。
在進入正式的證明之前,我們需要做以下的預備工作。首先,我們參照 [5, 6] 的做法,將神經網絡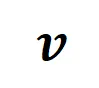 在特定樣本上的 inference 改寫為不同交互觸發函數的加權和:
在特定樣本上的 inference 改寫為不同交互觸發函數的加權和:
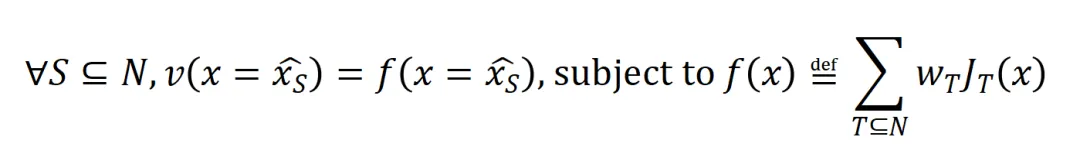
其中,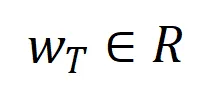 為標量權重,滿足
為標量權重,滿足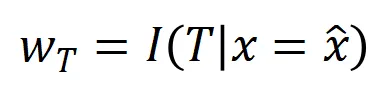 。而函數
。而函數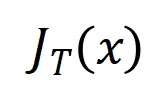 為交互觸發函數,在任意一個遮擋樣本
為交互觸發函數,在任意一個遮擋樣本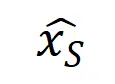 上都滿足
上都滿足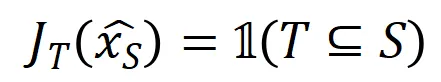 。函數
。函數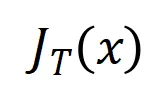 的具體形式可以由泰勒展開推導得到,可參考論文,這里不做贅述。
的具體形式可以由泰勒展開推導得到,可參考論文,這里不做贅述。
根據上述改寫形式,神經網絡在特定樣本上的學習可近似看成是對交互觸發函數的權重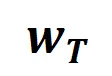 的學習。進一步地,實驗室的前期工作 [3] 發現在同一任務上充分訓練的不同的神經網絡往往會建模相似的交互,所以我們可以將神經網絡的學習看成是對一系列潛在的 ground truth 交互的擬合。由此,神經網絡在訓練到收斂時建模的交互可以看成是最小化下面的目標函數時得到的解:
的學習。進一步地,實驗室的前期工作 [3] 發現在同一任務上充分訓練的不同的神經網絡往往會建模相似的交互,所以我們可以將神經網絡的學習看成是對一系列潛在的 ground truth 交互的擬合。由此,神經網絡在訓練到收斂時建模的交互可以看成是最小化下面的目標函數時得到的解:
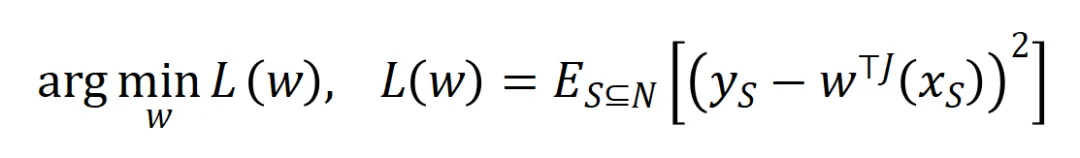
其中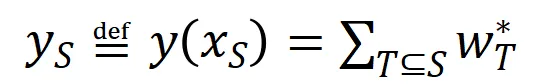 表示神經網絡需要擬合的一系列潛在的 ground truth 交互。
表示神經網絡需要擬合的一系列潛在的 ground truth 交互。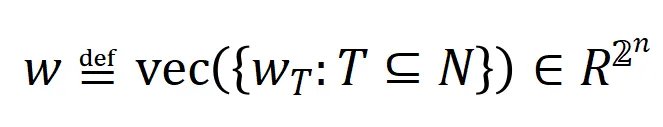 和
和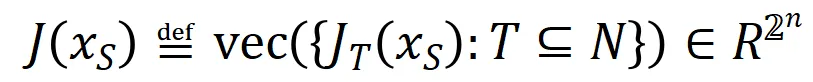 則分別表示將所有權重拼起來得到的向量和將所有交互觸發函數的值拼起來得到的向量。
則分別表示將所有權重拼起來得到的向量和將所有交互觸發函數的值拼起來得到的向量。
可惜的是,上述建模雖然能得到神經網絡訓練到收斂時的交互,但是無法很好地刻畫神經網絡訓練過程中學習交互的動態過程。這里引入我們的核心假設:我們假設初始化神經網絡的參數上包含了大量噪聲,而這些噪聲的量級在訓練過程中逐步變小。而進一步地,參數上的噪聲會導致交互觸發函數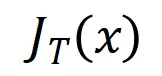 上的噪聲,且該噪聲隨著交互階數指數級增長 (在 [5] 中已有實驗上的觀察和驗證) 。我們將有噪聲下的神經網絡的學習建模如下:
上的噪聲,且該噪聲隨著交互階數指數級增長 (在 [5] 中已有實驗上的觀察和驗證) 。我們將有噪聲下的神經網絡的學習建模如下:
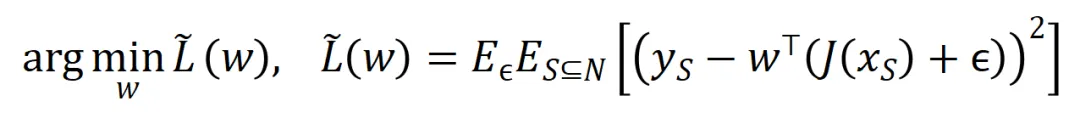
其中噪聲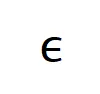 滿足
滿足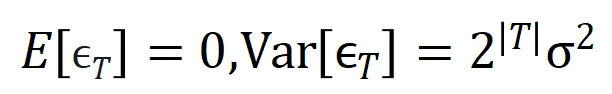 。且隨著訓練進行,噪聲的方差
。且隨著訓練進行,噪聲的方差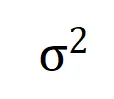 逐漸變小。
逐漸變小。
在給定的噪聲量級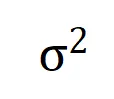 的情況下最小化上述損失函數,可得到最優交互權重
的情況下最小化上述損失函數,可得到最優交互權重 的解析解,如下圖中的定理所示。
的解析解,如下圖中的定理所示。

我們發現,隨著訓練進行(即噪聲量級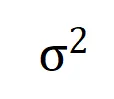 變小),中低階交互強度和高階交互強度的比值逐漸減小(如下面的定理所示)。這解釋了訓練的第二階段中神經網絡逐漸學到更加高階的交互的現象。
變小),中低階交互強度和高階交互強度的比值逐漸減小(如下面的定理所示)。這解釋了訓練的第二階段中神經網絡逐漸學到更加高階的交互的現象。

另外,我們對上述結論進一步做了實驗驗證。給定一個具有 n 個輸入單元的樣本,指標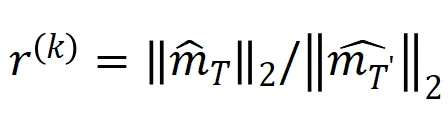 ,其中
,其中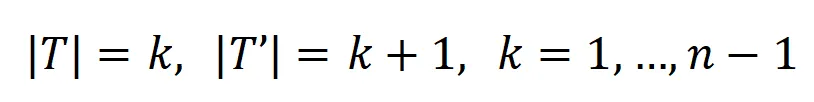 , 可以用來近似測量第 k 階交互和第 k+1 階交互強度的比值。在下圖中,我們可以發現,在不同的輸入單元個數 n 和不同的階數 k 下,該比值都會隨著
, 可以用來近似測量第 k 階交互和第 k+1 階交互強度的比值。在下圖中,我們可以發現,在不同的輸入單元個數 n 和不同的階數 k 下,該比值都會隨著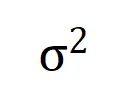 的減小而逐漸減小。
的減小而逐漸減小。

圖 9:在不同的輸入單元個數 n 和不同的階數 k 下,第 k 階交互和第 k+1 階交互強度的比值都會隨著噪聲量級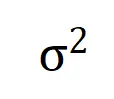 的減小而逐漸減小。這說明隨著訓練進行(即
的減小而逐漸減小。這說明隨著訓練進行(即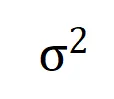 逐漸變小),低階交互強度與高階交互強度的比值逐漸變小,神經網絡逐漸學到更加高階的交互。
逐漸變小),低階交互強度與高階交互強度的比值逐漸變小,神經網絡逐漸學到更加高階的交互。
最后,我們對比了在不同噪聲量級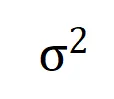 下的理論交互值
下的理論交互值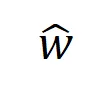 在各個階數上的分布
在各個階數上的分布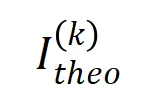 和實際訓練過程中各階交互的分布
和實際訓練過程中各階交互的分布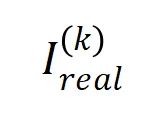 ,發現理論交互分布可以很好地預測實際訓練中各時間點的交互強度分布。
,發現理論交互分布可以很好地預測實際訓練中各時間點的交互強度分布。
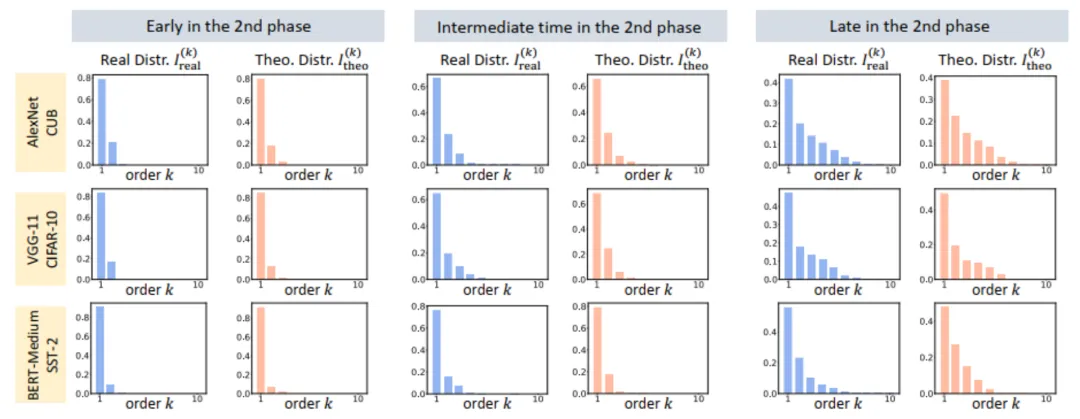
圖 10:比較理論交互分布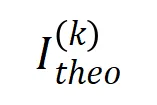 (藍色直方圖)和實際交互分布
(藍色直方圖)和實際交互分布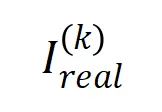 (橙色直方圖)。在訓練第二階段的不同時間點,理論交互分布都可以很好地預測和匹配實際交互的分布。更多結果請參見論文。
(橙色直方圖)。在訓練第二階段的不同時間點,理論交互分布都可以很好地預測和匹配實際交互的分布。更多結果請參見論文。
3. 證明神經網絡訓練的第一階段的交互變化動態過程。
如果說訓練的第二階段中交互的動態變化可以解釋為權重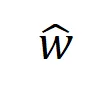 的最優解在噪聲
的最優解在噪聲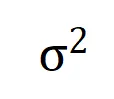 逐漸減小時的變化,那么第一階段就可認為是交互從初始化的隨機交互逐漸收斂到最優解的過程。
逐漸減小時的變化,那么第一階段就可認為是交互從初始化的隨機交互逐漸收斂到最優解的過程。
路漫漫其修遠兮,我們團隊是做神經網絡可解釋性的第一性原理,我們希望在更多的方面把這個理論做扎實,能夠嚴格證明等效交互是符號化的解釋,并且能夠解釋神經網絡的泛化性、魯棒性,同時證明神經網絡表征瓶頸,統一 12 種提升神經網絡對抗遷移性的方法和解釋 14 種重要性估計方法。我們后面會做出更扎實的工作,進一步完善理論體系。







































