最高提速1440倍!15秒用GCN搞定隨機規劃,中科院自動化所新成果入選ICML 24
僅需15秒即可搞定隨機規劃問題,速度比傳統方法快了1440倍!
中科院自動化研究所的新研究,利用GCN在此類問題上取得了新突破,論文已入選AI頂會ICML 2024。
這意味著,在條件不確定的情況下,也能實現高效決策。

不確定性下的決策是一類重要的決策問題,它要求決策者能夠充分考慮到所有的隨機情況并做出最合理的決策。
在數學領域,一種常用的解決方式是隨機規劃,也就是把隨機變量包含在數學規劃模型當中。
其中,兩階段隨機規劃(Two-Stage Stochastic Programming, 2SP)作為建模此類決策問題的有效方法,應用十分廣泛。
中科院自動化所的這項成果——HGCN2SP模型(HGCN代表分層圖卷積網絡),正是將2SP方法與圖卷積網絡結合,利用模型更高效地實現了此類問題求解。
論文第一作者為該所博士生吳洋,張一帆研究員是通訊作者。
什么是兩階段隨機規劃
隨機規劃的基本思想是將問題的未來可能情況轉化為若干個樣本場景,然后對每個樣本場景進行優化,最后綜合所有場景的優化結果來指導當前決策。
其應用領域包括供應鏈管理、金融投資、能源調度、災害應急管理等。
而兩階段隨機規劃,顧名思義就是把這個過程分成了兩個階段。
具體來說,這兩個階段分別要做出宏觀和微觀決策,以最小化總成本或最大化總收益。
第一階段的決策是在不確定性顯現之前做出的,目標是優化初始決策以適應未來可能發生的多種情況。
第二階段的決策是在不確定性顯現之后進行的,根據第一階段的決策和實際發生的情況進行調整,以優化整體結果。
通過2SP模型,決策者需要在決策過程中充分考慮可能發生的不同場景的影響,從而提高決策的魯棒性和靈活性,做出更為科學和高效的決策。
舉個例子,假設我們要從10個候選地點中選擇一些建立倉庫,以滿足周邊20個區域的需求。
第一階段需要決策的是,在這10個候選地點中應該選擇哪些;
第二階段則要確定倉庫和區域間的配送關系,此時的決策變量數量多達200個(即倉庫i是否配送區域j)。

△圖像由DALL·E生成
數學上,2SP問題通常表示為:
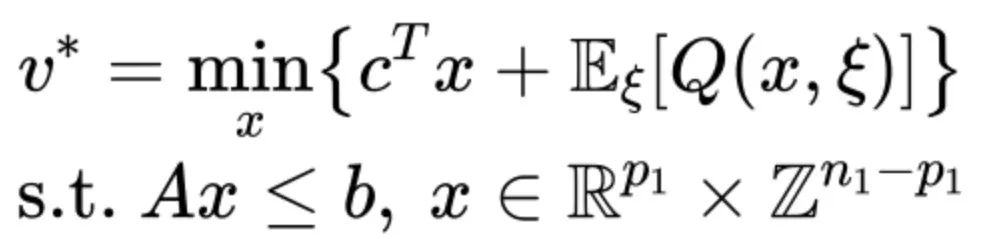
其中,Q(x,ξ)表示在給定第一階段決策x和場景ξ下的第二階段優化問題,其形式為:
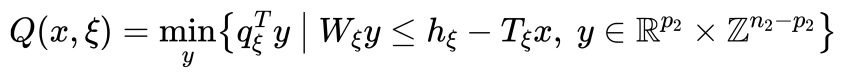
在實際的求解中,一般會采樣N個場景計算對應的Q值來近似期望。
顯然N越大則近似值越可信,但隨著場景數量的增加,問題規模迅速膨脹,會導致求解時間大幅提高。
還是用這個倉庫選址的問題來說明,為了能做出更好的選址決策,需要將需求、天氣、人流、交通等不確定因素考慮在內,而每一個因素的變化都對應著一個場景。
這意味著,需要廣泛采樣N個不同場景來盡可能模擬真實情況。這時,第二階段總決策變量數會高達200N個,使得求解時間極為漫長。
事實上,當N取500時,即使使用最先進的商用求解器Gurobi,也至少需要6個小時才能做出最優的決策。
傳統方法通常利用隨機采樣或聚類技術來挑選少量的場景(如10或20)以進行近似求解,雖然減少了時間,但得到的決策質量卻往往不理想。
基于此,也就有了HGCN2SP模型的設計思路——在減少采樣場景個數的同時,盡可能近似得到準確結果。
用圖卷積網絡解決2SP問題
研究團隊針對兩階段隨機規劃問題求解,提出了基于層次化圖卷積網絡的HGCN2SP模型。
具體的在算法設計方面,團隊通過構建層次圖來表征2SP問題,其中底層的圖用來表征每個場景的特性,而頂層的圖則用于表征場景之間的關系。
然后,再利用層次化圖卷積網絡(HGCN),分別挖掘底層場景子圖的嵌入信息和頂層場景空間的結構信息,以提取場景表示。
基于注意力機制的解碼器被用于按序挑選場景,不僅能找到具有代表性的場景來簡化問題,還可以通過優化場景的排列順序來改善單純形法求解問題時對初始基的選取,進而顯著提升求解時間。
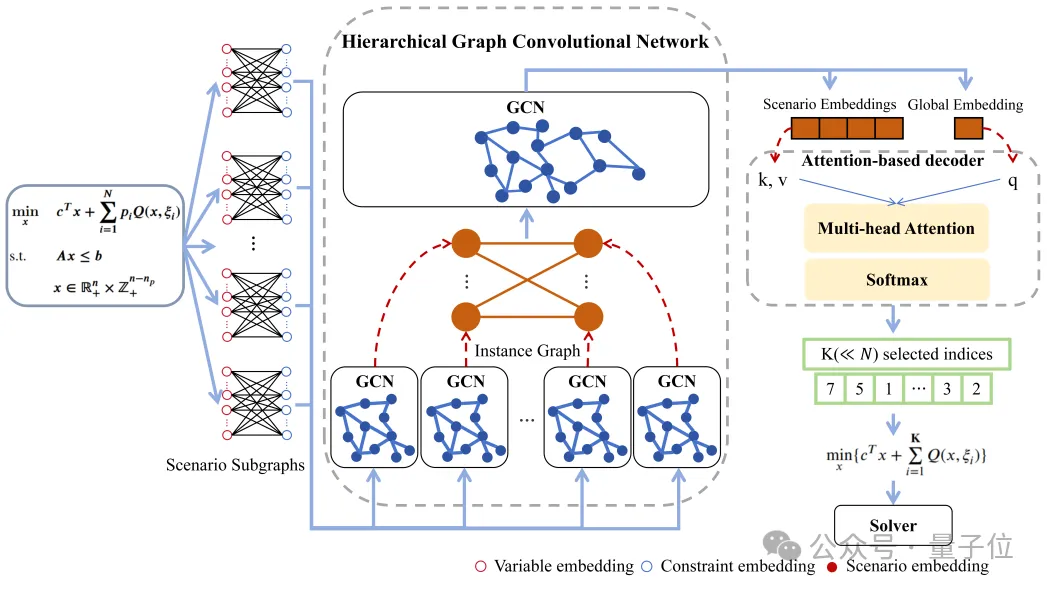
△HGCN2SP模型框架
團隊還結合強化學習(RL),綜合考察決策質量和求解時間來優化模型參數,顯著提高了問題求解的效率和質量。
在上述的倉庫選址問題中,盡管HGCN2SP只選取了10個場景,但其決策結果與Gurobi求解器用6個小時做出的決策差距僅為1.7%,而求解時間僅為15秒,相當于速度提升了1440倍,充分體現了該方法的有效性。
另外,在網絡設計問題(Network Design Problem, NDP)的實驗中,HGCN2SP僅用已有方法不到一半的時間得到了相近的決策效果。
尤其在大規模實例和大量場景情況下,HGCN2SP依然保持了強大的泛化能力。

HGCN2SP的提出為解決復雜的2SP問題提供了一種新的思路和工具,具有廣泛的應用前景。
研究團隊計劃進一步優化模型,降低訓練成本,并探索其在更多實際問題中的應用。
論文地址:https://openreview.net/forum?id=8onaVSFTEj