前些天，OpenAI 發(fā)布了 ο1 系列模型，它那「超越博士水平的」強(qiáng)大推理性能預(yù)示著其必將在人們的生產(chǎn)生活中大有作為。但它的使用成本也很高，以至于 OpenAI 不得不限制每位用戶的使用量：每位用戶每周僅能給 o1-preview 發(fā)送 30 條消息，給 o1-mini 發(fā)送 50 條消息。

實(shí)在是少！

為了降低 LLM 的使用成本，研究者們已經(jīng)想出了各式各樣的方法。有些方法的目標(biāo)是提升模型的效率，比如對(duì)模型進(jìn)行量化或蒸餾，但這種方法往往也伴隨著模型性能的下降。另一種思路則是提升運(yùn)行這些模型的硬件——英偉達(dá)正是這一路線的推動(dòng)者和受益者，但該公司的主要策略還是提升 GPU 的性能；另一些研究者則正在探索針對(duì) AI 構(gòu)建高效高性能的新型硬件體系。憶阻器（memristor）便是其中一個(gè)重要的研究方向。

憶阻器是一種電子元件，其能夠限制或調(diào)節(jié)電路中電流的流動(dòng)，并且可以記憶之前通過(guò)的電荷量。憶阻器在許多實(shí)際應(yīng)用中具有重要意義，原因之一是其具備非易失性特性，即在斷電情況下仍能保持記憶，這使得其在無(wú)電源或電源中斷時(shí)依然能夠持續(xù)使用。憶阻器被認(rèn)為是和電阻器、電容器、電感同層級(jí)的基礎(chǔ)電子元件。憶阻器的概念最早在 1971 年由華人科學(xué)家蔡少棠提出。

近日，Nature 發(fā)布了一篇來(lái)自印度科學(xué)學(xué)院、得克薩斯農(nóng)工大學(xué)和愛(ài)爾蘭利莫瑞克大學(xué)的一篇論文，其中提出了一種「線性對(duì)稱的自選擇式 14 bit 的動(dòng)力學(xué)分子憶阻器」。

論文標(biāo)題：Linear symmetric self-selecting 14-bit kinetic molecular memristors

論文地址：https://www.nature.com/articles/s41586-024-07902-2

該論文的核心亮點(diǎn)是，其中提出的分子憶阻器在核心的矩陣運(yùn)算上能實(shí)現(xiàn)遠(yuǎn)超電子器件效率的 14 bit 模擬計(jì)算；并且其實(shí)現(xiàn)了超過(guò) 73 dB 的信噪比，比之前的最佳水平直接高出了 4 個(gè)數(shù)量級(jí)，同時(shí)其能耗量比電子計(jì)算機(jī)低 460 倍！

這樣的出色表現(xiàn)讓 AI 工程師 Rohan Paul 忍不住驚嘆：「如果這是真的，算是到了 LLM 的真空管變硅晶體管時(shí)刻嗎？」

那么，這篇論文究竟提出了什么呢？真的有希望將 LLM 從高功耗高成本的困境中解脫出來(lái)嗎？讓我們來(lái)簡(jiǎn)單了解一下。

挑戰(zhàn)

我們知道，向量-矩陣乘法（VMM）是神經(jīng)網(wǎng)絡(luò)等許多計(jì)算算法的基礎(chǔ)。但是，VMM 很難實(shí)現(xiàn)，因?yàn)閷?duì)于長(zhǎng)度為 n 的向量，所需的計(jì)算步驟為 n2。盡管對(duì)稱運(yùn)算可以降低 VMM 的復(fù)雜性，但它們只適用于特定的矩陣結(jié)構(gòu)，比如人工智能中的非結(jié)構(gòu)化數(shù)據(jù)。

為了得到高效的通用型 VMM 引擎，人們一直在推動(dòng)硬件的發(fā)展，尤其是點(diǎn)積引擎（DPE）——一種可在單個(gè)時(shí)間步長(zhǎng)內(nèi)實(shí)現(xiàn) VMM 的模擬加速器。盡管 DPE 有應(yīng)對(duì)計(jì)算規(guī)模擴(kuò)展的潛力，但其應(yīng)用也受限于其精度，因?yàn)槟M電路元件僅提供 2-6 個(gè)等效比特。這種精度不足的根源在于其物理性質(zhì)不夠理想，包括非線性的權(quán)重更新、不對(duì)稱行為、噪聲、電導(dǎo)漂移和設(shè)備間差異。這是神經(jīng)形態(tài)計(jì)算的一個(gè)根本性挑戰(zhàn)。

為了解決這個(gè)問(wèn)題，需要發(fā)明一種能嵌入到電路中的元件，并且嵌入數(shù)量要比目前可用的模擬級(jí)別高出幾個(gè)數(shù)量級(jí)。

解決方案

該團(tuán)隊(duì)宣稱已經(jīng)發(fā)明出了這樣的元件。這是一種分子憶阻器交叉開(kāi)關(guān)矩陣，可集成在電路板中。其展現(xiàn)出了 14 比特的模擬精度、近乎理想的線性和對(duì)稱權(quán)重更新，以及每個(gè)電導(dǎo)層級(jí)的一步式可編程性（one-step programmability）。

如圖 1a 所示，該團(tuán)隊(duì)構(gòu)建了有史以來(lái)最大的分子憶阻器交叉開(kāi)關(guān)矩陣（64×64）結(jié)構(gòu)。使用的材料是夾在頂部和底部金電極之間的 60 nm 厚的 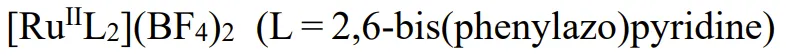薄膜。更多詳細(xì)的設(shè)計(jì)參數(shù)請(qǐng)參看原論文。

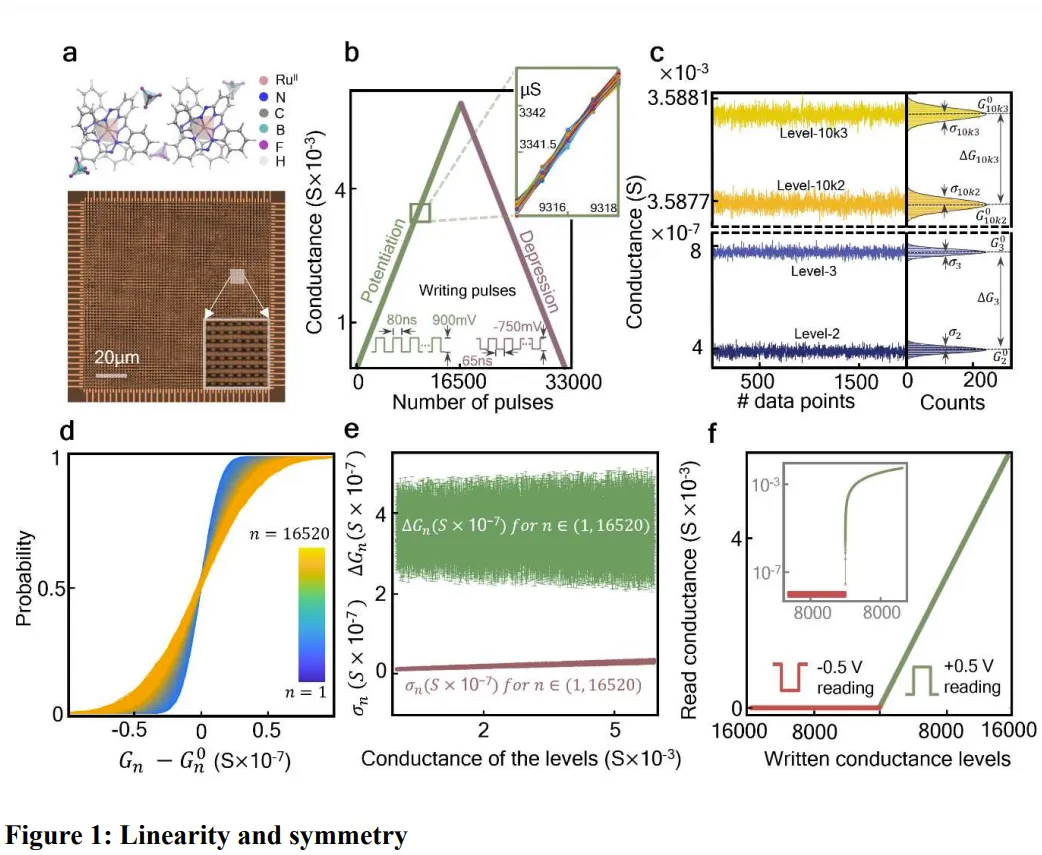
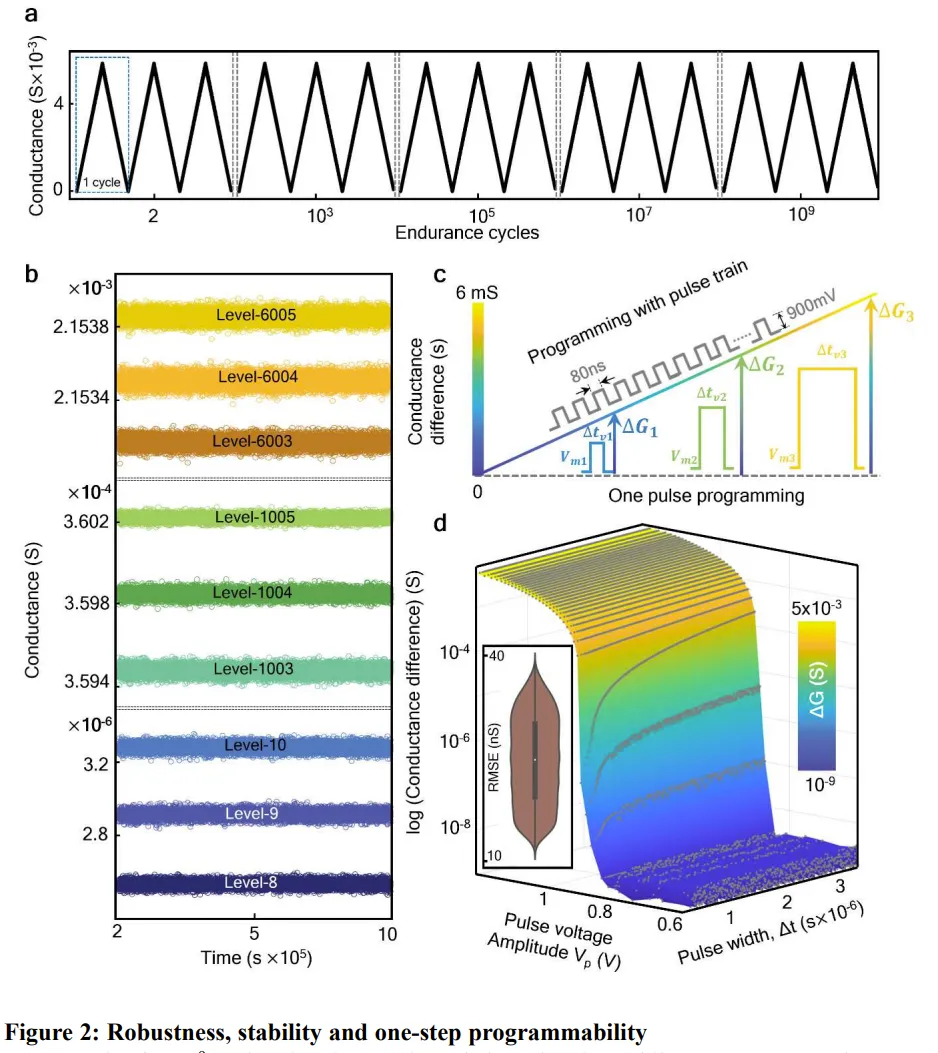
總之，該器件實(shí)現(xiàn)了想要的功能，并且具有相當(dāng)好的非易失性和穩(wěn)健性。如圖 2a 所示，這個(gè)交叉開(kāi)關(guān)矩陣耐久性很好，經(jīng)過(guò) 10^9 個(gè)操作周期后，權(quán)重更新特性依舊保持不變。另外，圖 2b 表明使用 500 mV 直流電壓在 85°C 環(huán)境下，該結(jié)構(gòu)能在 11 天內(nèi)不出現(xiàn)明顯的電導(dǎo)漂移。另外，他們還測(cè)試發(fā)現(xiàn)，其能維持長(zhǎng)達(dá) 7 個(gè)月的電導(dǎo)保持率。

實(shí)驗(yàn)

使用這個(gè) 64×64 的分子交叉開(kāi)關(guān)矩陣，該團(tuán)隊(duì)執(zhí)行了 VMM 實(shí)驗(yàn)，這用到了一個(gè)他們定制的超過(guò) 16 比特準(zhǔn)確度的混合信號(hào)外圍電路，如下圖 4 所示。a 圖是對(duì)其編程，使之執(zhí)行離散傅里葉變換（DFT）。b 圖則比較了計(jì)算出的 DFT 輸出與軟件計(jì)算的結(jié)果，可以看到它們之間非常一致，這表明這個(gè)結(jié)構(gòu)是有效的。

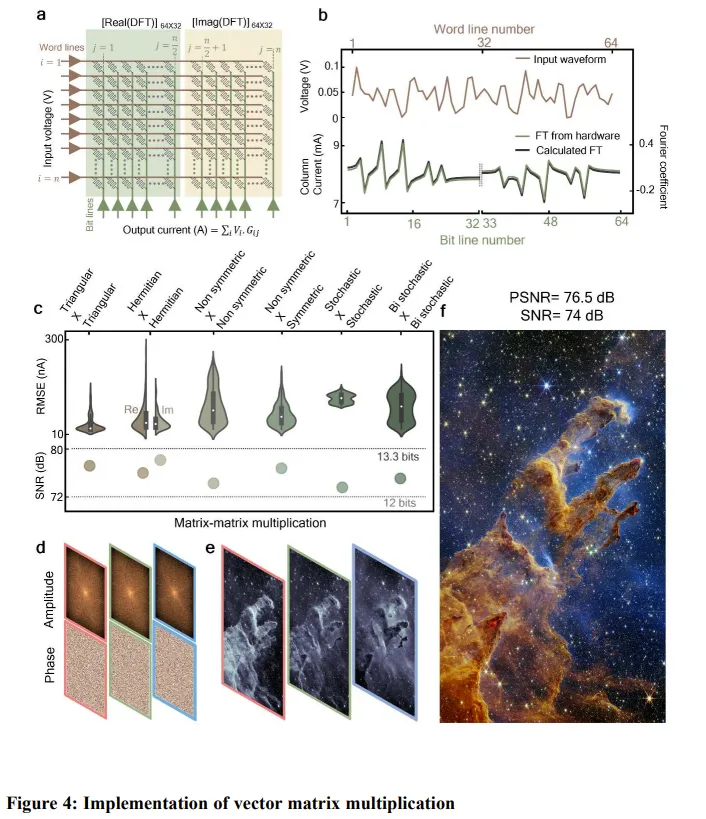
此外，他們還執(zhí)行了矩陣-矩陣乘法運(yùn)算，這是幾乎所有 AI 和機(jī)器學(xué)習(xí)算法的基礎(chǔ)運(yùn)算。結(jié)果發(fā)現(xiàn)，如果讓兩個(gè) 64×64 的矩陣相乘，則該結(jié)構(gòu)僅需要執(zhí)行 64 步，但如果讓電子計(jì)算機(jī)來(lái)干同樣的事，則需要執(zhí)行 262,144 次運(yùn)算。

圖 4c 表示其矩陣乘法的準(zhǔn)確度不依賴于對(duì)稱性，這是處理非結(jié)構(gòu)化數(shù)據(jù)的一個(gè)關(guān)鍵屬性。

該團(tuán)隊(duì)評(píng)估了不同矩陣組合，包括對(duì)稱、隨機(jī)和雙隨機(jī)矩陣。最終得到了 73-79 dB 的信噪比。該團(tuán)隊(duì)表示這是一個(gè)非常重大的進(jìn)步。

他們還展示了一個(gè)非常有趣的用例。使用矩陣乘法，他們使用從韋伯望遠(yuǎn)鏡數(shù)據(jù)庫(kù)檢索到的頻域數(shù)據(jù)，通過(guò)逆傅里葉變換重建了標(biāo)志性的「創(chuàng)生之柱」圖像，見(jiàn)圖 4d-f。

之所以選擇外太空數(shù)據(jù)，是因?yàn)樗狈?duì)稱性。這項(xiàng)任務(wù)每個(gè)平面都需要 26,256 個(gè)時(shí)間步驟，而數(shù)字計(jì)算機(jī)所需的步驟數(shù)超過(guò)了 10^8。

結(jié)果，他們得到的信噪比為 74 dB，峰值信噪比為 76.5 dB，直接高出了之前最佳的 DPE 4 個(gè)數(shù)量級(jí)。

這個(gè)轉(zhuǎn)譯過(guò)程的后續(xù)階段將需要進(jìn)一步擴(kuò)展這個(gè)交叉開(kāi)關(guān)矩陣，并開(kāi)發(fā)具有高精度的片上外圍電路。

該團(tuán)隊(duì)在論文中描述了一種經(jīng)過(guò)功率優(yōu)化的外圍電路設(shè)計(jì)，可以提供超高的能效：每秒每瓦 4.1 萬(wàn)億次運(yùn)算 (TOPS/W) 。這個(gè)數(shù)據(jù)比 18 核 Haswell CPU 高 460 倍，比當(dāng)前最高效的英偉達(dá) K80 GPU 高 220 倍，并且這還有很大的改進(jìn)空間。

這個(gè)示例展示了基于分子的技術(shù)的巨大潛力，通過(guò)將其集成到 CMOS 電路中，可以大幅超越最先進(jìn)的加速器的性能。

如果 OpenAI 等未來(lái)開(kāi)發(fā)的大模型也能運(yùn)行在基于此類技術(shù)開(kāi)發(fā)的硬件上，那 AI 的使用成本必定能下降很多。

更多研究細(xì)節(jié)、數(shù)據(jù)和代碼請(qǐng)?jiān)L問(wèn)原論文。