八種數(shù)值變量的特征工程技術(shù):利用Sklearn、Numpy和Python將數(shù)值轉(zhuǎn)化為預(yù)測模型的有效特征
特征工程是機器學(xué)習(xí)流程中的關(guān)鍵步驟,在此過程中,原始數(shù)據(jù)被轉(zhuǎn)換為更具意義的特征,以增強模型對數(shù)據(jù)關(guān)系的理解能力。
特征工程通常涉及對現(xiàn)有數(shù)據(jù)應(yīng)用轉(zhuǎn)換,以生成或修改數(shù)據(jù),這些轉(zhuǎn)換后的數(shù)據(jù)在機器學(xué)習(xí)和數(shù)據(jù)科學(xué)的語境下用于訓(xùn)練模型,從而提高模型性能。
本文主要介紹處理數(shù)值變量特征工程,將探討使用Python的Scikit-Learn庫、Numpy等工具處理數(shù)值的高級特征工程技術(shù),旨在提升機器學(xué)習(xí)模型的效能。

特征優(yōu)化是提升機器學(xué)習(xí)模型質(zhì)量的核心要素,尤其在分析復(fù)雜數(shù)據(jù)集時。有針對性地應(yīng)用特征工程技術(shù)可帶來以下優(yōu)勢:
- 揭示數(shù)據(jù)中的潛在模式:此技術(shù)能夠發(fā)現(xiàn)初步觀察中不易察覺的隱藏關(guān)系和結(jié)構(gòu)。
- 優(yōu)化變量表示:此過程將原始數(shù)據(jù)轉(zhuǎn)換為更適合機器學(xué)習(xí)的格式。
- 應(yīng)對數(shù)據(jù)分布和內(nèi)在特性相關(guān)的挑戰(zhàn):此方法解決了諸如偏度、異常值和變量可擴展性等問題。
精確實施這些特征優(yōu)化技術(shù)可顯著提升機器學(xué)習(xí)模型的性能。
這些改進體現(xiàn)在模型性能的多個方面,從預(yù)測能力到可解釋性。高質(zhì)量特征使模型能夠捕捉到數(shù)據(jù)中可能被忽視的細微差別和復(fù)雜模式。
特征優(yōu)化還有助于增強模型的穩(wěn)健性和泛化能力,這對于實際應(yīng)用至關(guān)重要,同時降低了過擬合的風(fēng)險。
接下來,我們將介紹一些實用的特征工程技術(shù)。
1、歸一化
歸一化(也稱為縮放)可能是數(shù)據(jù)科學(xué)家學(xué)習(xí)的第一個數(shù)值特征工程技術(shù)。這種方法通過減去平均值并除以標準差來調(diào)整變量。
執(zhí)行此轉(zhuǎn)換后,結(jié)果變量將具有0均值和1的標準差及方差。
在機器學(xué)習(xí)中,特別是深度學(xué)習(xí)領(lǐng)域,將變量限制在特定范圍內(nèi)(如僅在0和1之間)有助于模型更快地收斂到最優(yōu)解。這是一種學(xué)習(xí)型轉(zhuǎn)換 - 我們使用訓(xùn)練數(shù)據(jù)來推導(dǎo)正確的均值和標準差值,然后在應(yīng)用于新數(shù)據(jù)時使用這些值進行轉(zhuǎn)換。
需要注意的是,這種轉(zhuǎn)換不會改變分布,而是重新縮放了值。
我們將使用Sklearn的葡萄酒數(shù)據(jù)集進行分類任務(wù)。我們將比較使用和不使用混淆矩陣歸一化的性能,使用Sklearn實現(xiàn)。
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import confusion_matrix
import numpy as np
X, y = load_wine(return_X_y=True)
# 將數(shù)據(jù)劃分為訓(xùn)練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=42)
# 定義訓(xùn)練模型并獲取混淆矩陣的函數(shù)
def get_confusion_matrix(X_train, X_test, y_train, y_test):
model = KNeighborsClassifier(n_neighbors=5)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
return confusion_matrix(y_test, y_pred)
# 獲取未歸一化的混淆矩陣
cm_without_norm = get_confusion_matrix(X_train, X_test, y_train, y_test)
# 歸一化數(shù)據(jù)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# 獲取歸一化后的混淆矩陣
cm_with_norm = get_confusion_matrix(X_train_scaled, X_test_scaled, y_train, y_test)
# 創(chuàng)建兩個并列的子圖
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 8))
# 定義繪制熱圖的函數(shù)
def plot_heatmap(ax, cm, title):
sns.heatmap(cm, annot=True, fmt='d', cmap='viridis', ax=ax, cbar=False)
ax.set_title(title, fontsize=16, pad=20)
ax.set_xlabel(''Predicted', fontsize=12, labelpad=10)
ax.set_ylabel('Actual', fontsize=12, labelpad=10)
# 繪制熱圖
plot_heatmap(ax1, cm_without_norm, 'Confusion Matrix\nWithout Normalization')
plot_heatmap(ax2, cm_with_norm, 'Confusion Matrix\nWith Normalization')
# 添加共用的顏色條
cbar_ax = fig.add_axes([0.92, 0.15, 0.02, 0.7])
sm = plt.cm.ScalarMappable(cmap='viridis', norm=plt.Normalize(vmin=0, vmax=np.max([cm_without_norm, cm_with_norm])))
fig.colorbar(sm, cax=cbar_ax)
# 調(diào)整布局并顯示圖表
plt.tight_layout(rect=[0, 0, 0.9, 1])
plt.show()
性能提升約為30% - 對某些算法而言,歸一化的影響如此顯著,以至于不正確地應(yīng)用它可能導(dǎo)致數(shù)據(jù)科學(xué)家犯嚴重錯誤。
歸一化還有一些變體。在Sklearn中,這些變體被稱為
RobustScaler和MinMaxScaler。
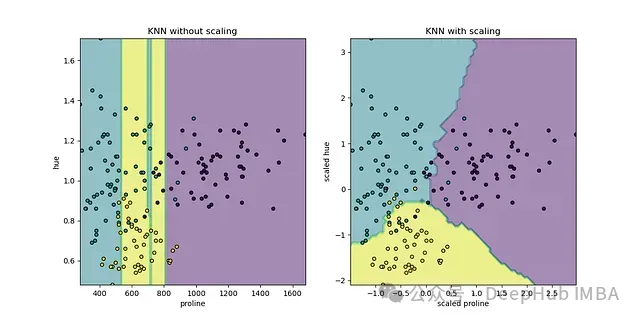
Sklearn示例中提供了一個更復(fù)雜的圖表,展示了歸一化和未歸一化的KNNClassifier模型的分類邊界對比
2、多項式特征
多項式特征是一種在線性模型中引入非線性的有效方法。Scikit-Learn的PolynomialFeatures類能夠生成多項式特征和變量間的交互項。
常見的多項式特征包括:
- x 2 (平方項)
- x 3 (立方項)
- x ? (四次方項)
- 更高次項
對于具有多個特征的模型(x_1, x_2, …, x_n),還可以創(chuàng)建交互項:
- _x__ 1 × _x__ 2 (一階交互項)
- _x__ 12 × _x__ 2 (二階交互項)
- _x__ 1 × _x__ 22 (二階交互項)
- 更高階交互項
多項式特征的主要目標是使線性模型能夠?qū)W習(xí)數(shù)據(jù)中的非線性關(guān)系,而無需改變底層算法。
多項式特征的主要優(yōu)勢在于顯著增加了模型的靈活性,使線性模型能夠捕捉數(shù)據(jù)中的非線性關(guān)系。具體表現(xiàn)為:
- 能夠在特征空間中建模復(fù)雜的曲線和曲面
- 對本質(zhì)上非線性的數(shù)據(jù)可能產(chǎn)生積極的性能貢獻
- 模型在捕捉非線性關(guān)系的同時保持線性的基礎(chǔ)結(jié)構(gòu)。這允許使用熟悉的分析工具,并且比復(fù)雜的非線性模型更容易解釋系數(shù),盡管這種簡單性隨著多項式次數(shù)的增加而降低。
另一個關(guān)鍵優(yōu)勢是能夠揭示變量之間隱藏的交互。在物理學(xué)或經(jīng)濟學(xué)等領(lǐng)域,關(guān)系通常是非線性的,這個特性尤為有價值。
但是多項式特征也存在一些缺點:
- 它迅速增加了數(shù)據(jù)集的維度,為每個輸入特征創(chuàng)建額外的列
- 過度使用可能導(dǎo)致過擬合
- 由于需要處理更多的特征,計算資源需求增加
從實際角度來看,多項式特征的實現(xiàn)相對簡單,這要歸功于Python中的Sklearn庫。下面我們將展示如何實現(xiàn)它。
PolynomialFeatures是Scikit-learn中用于生成多項式特征的類,位于sklearn.preprocessing模塊中。
該類將一維輸入數(shù)組轉(zhuǎn)換為包含所有多項式項(直至指定次數(shù))的新數(shù)組。例如,如果原始特征是[a, b],次數(shù)為2,則結(jié)果特征將是[1, a, b, a2, ab, b2]。
該類的主要參數(shù)如下:
- degree (int, 默認=2):多項式的次數(shù)。 確定生成的多項式項的最高次數(shù)。
- interaction_only (bool, 默認=False):如果為True,則僅生成交互項。不產(chǎn)生單個特征的冪。
- include_bias (bool, 默認=True):如果為True,包括一列1(偏置項)。在使用沒有單獨截距項的模型時有用。
- order (C或F, 默認=C):確定特征的輸出順序。C表示C風(fēng)格順序(最后的特征變化最快),'F'表示Fortran風(fēng)格順序。
以下是在Sklearn中實現(xiàn)該類的示例:
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
X = np.array([[1, 2], [3, 4]])
poly = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly.fit_transform(X)
print(X_poly)
# 輸出: [[1. 2. 1. 2. 4.]
# [3. 4. 9. 12. 16.]]
print(poly.get_feature_names(['x1', 'x2']))
# 輸出: ['x1', 'x2', 'x1^2', 'x1 x2', 'x2^2']這些生成的特征可以為機器學(xué)習(xí)模型提供額外的信息,潛在地提高其性能。
3、FunctionTransformer
FunctionTransformer是Scikit-learn中的一個多功能工具,允許將自定義函數(shù)集成到數(shù)據(jù)轉(zhuǎn)換過程中。它能夠?qū)⑷我夂瘮?shù)應(yīng)用于數(shù)據(jù),作為預(yù)處理或特征工程管道的一部分。它將Python函數(shù)轉(zhuǎn)換為與Scikit-learn API兼容的"轉(zhuǎn)換器"對象(這里的Transformer不同于深度學(xué)習(xí)模型,而是指Sklearn中的轉(zhuǎn)換器概念)。
FunctionTransformer以Python函數(shù)為主要輸入,創(chuàng)建一個轉(zhuǎn)換器對象。當(dāng)應(yīng)用于數(shù)據(jù)時,這個對象執(zhí)行指定的函數(shù)。它可以與其他轉(zhuǎn)換器結(jié)合使用,或在Scikit-learn管道中使用。
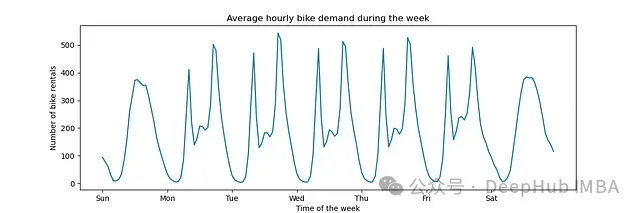
一個具體的應(yīng)用例子是將該對象應(yīng)用于時間序列以提取三角函數(shù)特征。
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 4))
average_week_demand = df.groupby(["weekday", "hour"])["count"].mean()
average_week_demand.plot(ax=ax)
_ = ax.set(
title="Average hourly bike demand during the week",
xticks=[i * 24 for i in range(7)],
xticklabels=["Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"],
xlabel="Time of the week"
)
FunctionTransformer的典型應(yīng)用包括:
- 創(chuàng)建復(fù)雜或領(lǐng)域特定的特征
- 對數(shù)據(jù)應(yīng)用非標準數(shù)學(xué)運算
- 將現(xiàn)有的預(yù)處理邏輯集成到Scikit-learn管道中
FunctionTransformer充當(dāng)了自定義Python函數(shù)和Scikit-learn函數(shù)之間的橋梁,為數(shù)據(jù)預(yù)處理和特征工程提供了靈活性。
以下代碼展示了如何應(yīng)用函數(shù)來創(chuàng)建上述時間序列的三角函數(shù)轉(zhuǎn)換:
import numpy as np
import pandas as pd
from sklearn.preprocessing import FunctionTransformer
import matplotlib.pyplot as plt
def sin_transformer(period):
return FunctionTransformer(lambda x: np.sin(x / period * 2 * np.pi))
def cos_transformer(period):
return FunctionTransformer(lambda x: np.cos(x / period * 2 * np.pi))
hour_df = pd.DataFrame(
np.arange(26).reshape(-1, 1),
columns=["hour"],
)
hour_df["hour_sin"] = sin_transformer(24).fit_transform(hour_df)["hour"]
hour_df["hour_cos"] = cos_transformer(24).fit_transform(hour_df)["hour"]
hour_df.plot(x="hour")
_ = plt.title("Trigonometric encoding of the 'hour' feature")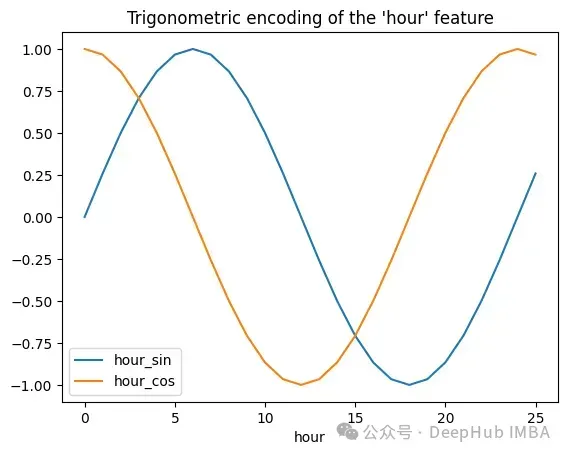
FunctionTransformer在時間序列分析中有廣泛的應(yīng)用。
4、KBinsDiscretizer
KBinsDiscretizer是Scikit-learn中的一個預(yù)處理類,設(shè)計用于將連續(xù)特征轉(zhuǎn)換為離散分類特征。這個過程被稱為離散化、量化或分箱。某些具有連續(xù)特征的數(shù)據(jù)集可能會從離散化中受益,因為它可以將具有連續(xù)屬性的數(shù)據(jù)集轉(zhuǎn)換為僅具有名義屬性的數(shù)據(jù)集。
其主要目標是將連續(xù)變量的范圍劃分為特定數(shù)量的區(qū)間(或箱)。每個原始值都被替換為它所屬的箱的標簽。
該算法的工作原理如下:
- 分析連續(xù)特征的分布
- 基于這個分布創(chuàng)建預(yù)定義數(shù)量的箱
- 將每個原始值分配到適當(dāng)?shù)南渲?/span>
- 用箱標簽或箱的獨熱編碼替換原始值
關(guān)鍵參數(shù):
n_bins:要創(chuàng)建的箱數(shù)。可以是整數(shù)或整數(shù)數(shù)組,用于每個特征的不同箱數(shù)。
encode:編碼箱的方法(onehot、ordinal或onehot-dense)。
- onehot:使用獨熱編碼對轉(zhuǎn)換后的結(jié)果進行編碼,并返回稀疏矩陣。被忽略的特征總是堆疊在右側(cè)。
- onehot-dense:使用獨熱編碼對轉(zhuǎn)換后的結(jié)果進行編碼,并返回"密集"數(shù)組(即非稀疏格式)。
- ordinal:返回編碼為整數(shù)值的箱。
strategy:定義箱邊界的策略(uniform、quantile或kmeans)。
- uniform:創(chuàng)建等寬的箱。
- quantile:為每個特征創(chuàng)建包含相同數(shù)量點的箱。
- kmeans:使用k-means聚類定義箱。
需要考慮的因素:
- 箱數(shù)和策略的選擇會顯著影響結(jié)果。
- 可能導(dǎo)致信息損失,尤其是在箱數(shù)很少的情況下(類似于使用很少的組繪制直方圖時)。
- 對于對非正態(tài)分布或非線性關(guān)系敏感的算法特別有用。
我們將通過觀察線性回歸和決策樹在學(xué)習(xí)連續(xù)模式與離散化模式時的性能來展示應(yīng)用。創(chuàng)建一個隨機但半線性數(shù)字的模擬數(shù)據(jù)集,將模型應(yīng)用于連續(xù)數(shù)據(jù),然后將相同的數(shù)據(jù)集應(yīng)用于離散化特征。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeRegressor
# 設(shè)置隨機數(shù)生成器以確保可重復(fù)性
rnd = np.random.RandomState(42)
# 創(chuàng)建數(shù)據(jù)集
X = rnd.uniform(-3, 3, size=100) # 在-3和3之間的100個點
y = np.sin(X) + rnd.normal(size=len(X)) / 3 # 正弦函數(shù)加噪聲
X = X.reshape(-1, 1) # 重塑為sklearn所需的正確格式
# 應(yīng)用KBinsDiscretizer
discretizer = KBinsDiscretizer(n_bins=10, encode="onehot")
X_binned = discretizer.fit_transform(X)
# 準備可視化
fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True, figsize=(12, 5))
line = np.linspace(-3, 3, 1000).reshape(-1, 1) # 用于繪圖的點
# 訓(xùn)練和繪制模型的函數(shù)
def train_and_plot(X_train, X_plot, ax, title):
# 線性回歸
linear_reg = LinearRegression().fit(X_train, y)
ax.plot(line, linear_reg.predict(X_plot), linewidth=2, color="green", label="Linear Regression")
# 決策樹
tree_reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X_train, y)
ax.plot(line, tree_reg.predict(X_plot), linewidth=2, color="red", label="Decision Tree")
# 原始數(shù)據(jù)
ax.plot(X[:, 0], y, "o", c="k", alpha=0.5)
ax.legend(loc="best")
ax.set_xlabel("Input Feature")
ax.set_title(title)
# 繪制原始數(shù)據(jù)的圖
train_and_plot(X, line, ax1, "Results Before Discretization")
ax1.set_ylabel("Regression Output")
# 繪制離散化數(shù)據(jù)的圖
line_binned = discretizer.transform(line)
train_and_plot(X_binned, line_binned, ax2, "Results After Discretization")
plt.tight_layout()
plt.show()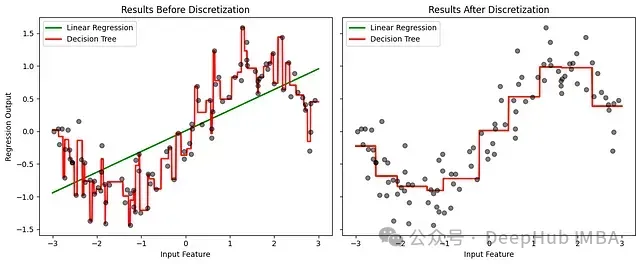
線性回歸在離散化后顯著改善,更好地捕捉了非線性。決策樹顯示的變化較小,因為它本身就能處理非線性。這個例子說明了離散化如何幫助線性模型捕捉非線性關(guān)系,在某些情況下可能會提高性能。
5、對數(shù)變換
對數(shù)變換的主要優(yōu)勢在于其壓縮值范圍的能力,這對于具有高可變性或異常值的數(shù)據(jù)特別有用。
- 范圍壓縮:對數(shù)變換減少了最大值之間的距離,同時保持較小值相對不變。有助于規(guī)范化偏斜分布,使右尾分布更對稱,更接近正態(tài)分布。
- 線性化:它可以將非線性關(guān)系線性化。它將指數(shù)關(guān)系轉(zhuǎn)換為線性關(guān)系,簡化了分析并提高了假設(shè)變量之間線性關(guān)系的模型的性能。
- 處理異常值:該變換有效地管理極端數(shù)據(jù),允許處理異常值而無需刪除,從而保留潛在的重要信息。
- 數(shù)學(xué)定義:最常見的對數(shù)變換使用自然對數(shù)(以e為底),定義為 y =ln(x),其中 x 是原始值,y 是變換后的值。請注意,這種變換僅對正值的 x 定義,如果存在零或負值,可能需要添加常數(shù)。
- 特征縮放:它可以用作特征縮放技術(shù),補充或替代標準化或最小-最大規(guī)范化等方法。可以提高線性回歸等模型的性能,這些模型受益于具有更對稱分布的特征。
在機器學(xué)習(xí)中,當(dāng)想要規(guī)范化一個不是自然分布的分布時,通常會使用對數(shù)變換。
例如,一個眾所周知的不正態(tài)分布的變量是年收入 —— 你經(jīng)常想要對這個變量建模以提供價值預(yù)測,但使用這種分布工作并不方便,特別是如果你使用不能正確建模非線性數(shù)據(jù)的算法。
通過對數(shù)變換,使用numpy,可以趨向正態(tài)分布,使變量更容易預(yù)測。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 創(chuàng)建一個具有正偏度值的示例數(shù)據(jù)集
np.random.seed(42)
data = {
'Income': np.random.exponential(scale=50000, size=1000) # 指數(shù)分布以模擬偏度
}
df = pd.DataFrame(data)
# 創(chuàng)建一個具有兩個并排子圖的圖形
fig, axes = plt.subplots(1, 2, figsize=(15, 5))
# 原始分布的圖
axes[0].hist(df['Income'], bins=50, color='blue', alpha=0.7)
axes[0].set_title('Original Income Distribution')
axes[0].set_xlabel('Income')
axes[0].set_ylabel('Frequency')
# 應(yīng)用對數(shù)變換
df['Log_Income'] = np.log1p(df['Income']) # log1p相當(dāng)于log(x + 1)
# 變換后分布的圖
axes[1].hist(df['Log_Income'], bins=50, color='green', alpha=0.7)
axes[1].set_title('Log-transformed Income Distribution')
axes[1].set_xlabel('Log_Income')
axes[1].set_ylabel('Frequency')
# 顯示圖形
plt.tight_layout()
plt.show()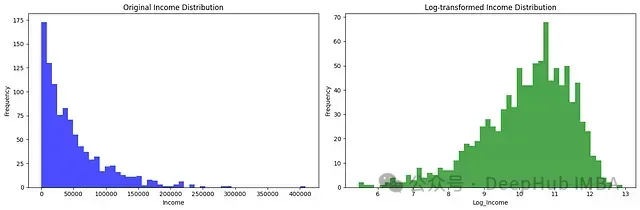
6、PowerTransformer
PowerTransformer是Sklearn preprocessing模塊中的一個類,包含用于使數(shù)據(jù)更接近高斯分布的邏輯。這對于建模與異方差(即非恒定方差)相關(guān)的問題或其他需要正態(tài)性的情況很有用。
,PowerTransformer支持Box-Cox和Yeo-Johnson變換。使用最大似然(對數(shù)似然)估計最優(yōu)參數(shù)以穩(wěn)定方差并最小化偏度。
Box-Cox要求輸入數(shù)據(jù)嚴格為正,而Yeo-Johnson支持正負數(shù)據(jù)。
在機器學(xué)習(xí)的背景下,這些變換解決了幾個常見挑戰(zhàn):
- 數(shù)據(jù)規(guī)范化: 許多機器學(xué)習(xí)算法,如線性回歸、神經(jīng)網(wǎng)絡(luò)和一些聚類方法,假設(shè)數(shù)據(jù)遵循正態(tài)分布。PowerTransformer可以將偏斜或重尾分布轉(zhuǎn)換為更接近高斯分布的形狀,這可以提高這些模型的性能。
- 方差穩(wěn)定化: 在真實數(shù)據(jù)集中,特征的方差通常隨其幅度變化,這種現(xiàn)象稱為異方差。這可能會影響許多算法的有效性。PowerTransformer有助于穩(wěn)定方差,使其在特征值的不同范圍內(nèi)更加一致。
- 關(guān)系線性化: 一些算法,如線性回歸,假設(shè)變量之間存在線性關(guān)系。PowerTransformer可以將非線性關(guān)系線性化,擴大這些模型在更復(fù)雜數(shù)據(jù)集上的適用性。
Box-Cox變換
Box-Cox變換是一系列冪變換,可以穩(wěn)定方差并使數(shù)據(jù)更接近正態(tài)分布。它在數(shù)學(xué)上定義為:
- y(λ) = (y λ — 1) / λ 如果 y ≠ 0
- y(λ) = log(y) 如果 y = 0
其中:
- x 是原始值,
- y 是變換后的值,
- λ 是變換參數(shù)
Box-Cox變換應(yīng)用于正數(shù)據(jù),并要求從數(shù)據(jù)中估計參數(shù)λ,以找到使數(shù)據(jù)正態(tài)化的最佳變換。
PowerTransformer的行為類似于Sklearn估計器,支持.fit()和.transform()方法。
Yeo-Johnson變換基于Box-Cox變換,但允許負值。本文不會詳細介紹Yeo-Johnson變換。
如前所述,Yeo-Johnson變換基于Box-Cox變換,但lambda可以取的值可能會改變。這使得這些變換本質(zhì)上不同,因為它們可能給出不同的結(jié)果。
在Python中,只需將其中一種變換方法作為字符串傳遞給PowerTransformer對象
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PowerTransformer
# 生成包含正值和負值的數(shù)據(jù)
np.random.seed(42)
data_positive = np.random.exponential(scale=2, size=1000) # 正值
data_negative = -np.random.exponential(scale=0.5, size=200) # 負值
data = np.concatenate([data_positive, data_negative]) # 合并正值和負值數(shù)據(jù)
# 創(chuàng)建兩個PowerTransformer實例:一個用于Yeo-Johnson,一個用于Box-Cox進行比較
pt_yj = PowerTransformer(method='yeo-johnson', standardize=False) # Yeo-Johnson變換
pt_bc = PowerTransformer(method='box-cox', standardize=False) # Box-Cox變換
# 應(yīng)用變換
data_yj = pt_yj.fit_transform(data.reshape(-1, 1)) # 應(yīng)用Yeo-Johnson變換
# Box-Cox需要正數(shù)據(jù),所以我們添加一個偏移量使所有值為正
data_offset = data - np.min(data) + 1e-6 # 偏移量以確保所有值為正
data_bc = pt_bc.fit_transform(data_offset.reshape(-1, 1)) # 應(yīng)用Box-Cox變換
# 可視化結(jié)果
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 5))
# 原始數(shù)據(jù)的直方圖
ax1.hist(data, bins=50, edgecolor='black')
ax1.set_title("Original Data")
ax1.set_xlabel("Value")
ax1.set_ylabel("Frequency")
# Yeo-Johnson變換后數(shù)據(jù)的直方圖
ax2.histax2.hist(data_yj, bins=50, edgecolor='black')
ax2.set_title("Yeo-Johnson")
ax2.set_xlabel("Value")
# Box-Cox變換后數(shù)據(jù)的直方圖
ax3.hist(data_bc, bins=50, edgecolor='black')
ax3.set_title("Box-Cox")
ax3.set_xlabel("Value")
plt.tight_layout()
plt.show()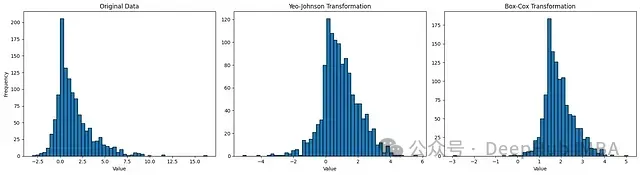
7、QuantileTransformer
分位數(shù)變換將一個變量的分布映射到另一個目標分布。使用Sklearn的QuantileTransformer類,可以將非正態(tài)分布轉(zhuǎn)換為所需的分布。
考慮任何事件分布 —— 這個分布中的每個事件都會有一個與之相關(guān)的發(fā)生概率。這種行為由累積分布函數(shù)(CDF)定義,每種分布的CDF都不同。
分位數(shù)函數(shù)是CDF的逆:而CDF是一個返回值等于或小于給定值的概率的函數(shù),PPF(百分位點函數(shù))是這個函數(shù)的逆,返回等于或小于給定概率的值。
在異常值檢測的背景下,QuantileTransformer可用于轉(zhuǎn)換數(shù)據(jù)以使其更加可見。通過將數(shù)據(jù)轉(zhuǎn)換為均勻分布,異常值將被映射到分布的極端,使它們與內(nèi)部點更容易區(qū)分。
QuantileTransformer可以將任意分布強制轉(zhuǎn)換為高斯分布,前提是有足夠的訓(xùn)練樣本(數(shù)千個)。由于它是一種非參數(shù)方法,比參數(shù)方法(Box-Cox和Yeo-Johnson)更難解釋。
Sklearn再次為我們提供了專用的QuantileTransformer對象,其中一個重要參數(shù)是output_distribution,它可以接受"uniform"或"normal"值。這些代表數(shù)據(jù)被映射到的分布。
import numpy as np
from sklearn.preprocessing import QuantileTransformer
import matplotlib.pyplot as plt
# 創(chuàng)建一個具有偏斜分布的樣本數(shù)據(jù)集
np.random.seed(0)
data = np.random.exponential(scale=2, size=(1000, 1)) # 指數(shù)分布
# 初始化QuantileTransformer
quantile_transformer = QuantileTransformer(n_quantiles=100, output_distribution='normal')
# 應(yīng)用變換
data_transformed = quantile_transformer.fit_transform(data)
# 可視化原始和變換后的數(shù)據(jù)
plt.figure(figsize=(12, 6))
# 原始數(shù)據(jù)的直方圖
plt.subplot(1, 2, 1)
plt.hist(data, bins=50, color='blue', edgecolor='black')
plt.title("Original Data (Exponential)")
# 變換后數(shù)據(jù)的直方圖
plt.subplot(1, 2, 2)
plt.hist(data_transformed, bins=50, color='green', edgecolor='black')
plt.title("Transformed Data (Normal)")
plt.show()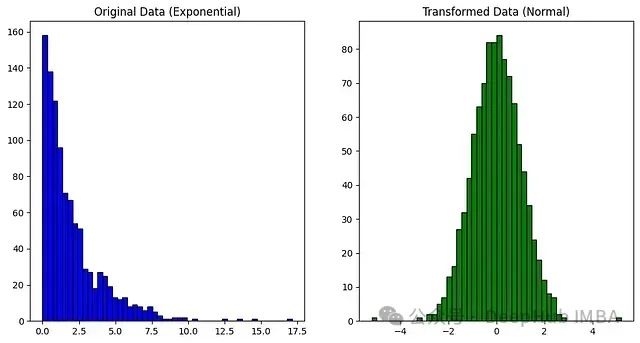
變換示例:從特定分布到正態(tài)分布
下面是一個圖形可視化,比較了不同的非正態(tài)分布及其相對變換,通過我們探討的一些技術(shù)。
我使用Sklearn文檔中的圖像作為參考,修改了圖表的排序以便于閱讀。
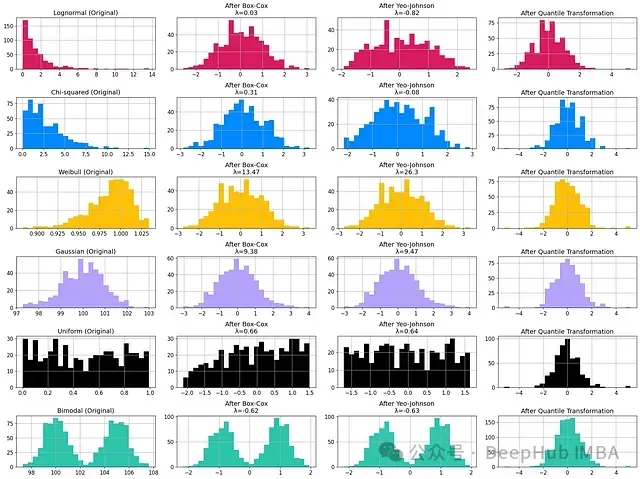
這張圖突出顯示了某些變換的局限性,但是它們并不總是成功。例如對于雙峰分布,除了分位數(shù)變換外,所有嘗試轉(zhuǎn)換為正態(tài)曲線的努力都失敗了。
8、主成分分析 PCA
主成分分析(PCA)將一組可能相關(guān)的變量轉(zhuǎn)換為一組線性不相關(guān)的變量,稱為主成分。這些主成分按順序排列,使得前幾個包含原始變量中存在的大部分方差。
在特征工程的背景下,PCA可以用于減少特征數(shù)量,同時保留大部分信息。這可能會減少數(shù)據(jù)中的噪聲和可能混淆模型的低級相關(guān)性。
作為一種降維技術(shù),PCA應(yīng)該用于壓縮數(shù)據(jù)集而不是擴展它。PCA可以提取一些潛在特征,這些特征是影響您的數(shù)據(jù)的隱藏或潛在因素。例如有一個圖像數(shù)據(jù)集,可以使用PCA來找到代表圖像中對象的形狀、顏色或紋理的特征。這些潛在特征可以幫助您更好地理解數(shù)據(jù)并改進機器學(xué)習(xí)模型。
PCA不僅可以應(yīng)用在表格類數(shù)據(jù),它還可以作為特征工程應(yīng)用是在處理圖像中。
讓我們?nèi)klearn lfw_people數(shù)據(jù)集中存在的隨機人臉,可以使用TruncatedSVD(一種與PCA非常相似的壓縮技術(shù))來提取關(guān)鍵圖像特征,如邊緣、陰影和主要對象的位置,為機器學(xué)習(xí)模型提供相關(guān)信息進行建模。
這種方法的一個典型應(yīng)用是規(guī)范化圖像,使系統(tǒng)對光照或其他條件的變化更加穩(wěn)健 —— 這使得減少的人臉成為最終面部識別的基礎(chǔ)。

從Sklearn的開放LFW數(shù)據(jù)集中隨機選取的圖像。
創(chuàng)建此可視化的Python代碼:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import TruncatedSVD
# 加載Labeled Faces in the Wild數(shù)據(jù)集
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)
X = lfw_people.data
n_samples, h, w = lfw_people.images.shape
print(f"數(shù)據(jù)集維度:{X.shape}")
# 用于降維的組件數(shù)
n_components = 50
# 應(yīng)用TruncatedSVD
svd = TruncatedSVD(n_components=n_components, random_state=42)
X_transformed = svd.fit_transform(X)
# 重構(gòu)圖像的函數(shù)
def reconstruct_image(svd, X_transformed):
return np.dot(X_transformed, svd.components_)
# 重構(gòu)所有圖像
X_reconstructed = reconstruct_image(svd, X_transformed)
# 顯示原始和降維人臉的函數(shù)
def plot_transposed_original_and_reduced(X_original, X_reduced, n_faces=5):
fig, axes = plt.subplots(2, n_faces, figsize=(3*n_faces, 6))
random_indices = np.random.choice(X_original.shape[0], n_faces, replace=False)
for i, idx in enumerate(random_indices):
# 原始人臉
axes[0, i].imshow(X_original[idx].reshape(h, w), cmap='gray')
axes[0, i].set_title(f'Face {i+1}\nOriginal')
axes[0, i].axis('off')
# 降維人臉
axes[1, i].imshow(X_reduced[idx].reshape(h, w), cmap='gray')
axes[1, i].set_title(f'Reduced\n({n_components} comp.)')
axes[1, i].axis('off')
plt.tight_layout()
plt.show()
# 顯示原始和降維人臉
plot_transposed_original_and_reduced(X, X_reconstructed)
# 計算并打印平均重構(gòu)誤差
mse = np.mean((X - X_reconstructed) ** 2)
print(f"\n平均重構(gòu)誤差 (MSE):{mse:.4f}")
# 打印累積解釋方差
explained_variance_ratio = svd.explained_variance_ratio_
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)
print(f"\n{n_components} 個組件的累積解釋方差:{cumulative_variance_ratio[-1]:.4f}")
# 顯示前幾個組件
n_components_show = min(10, n_components)
components = svd.components_[:n_components_show].reshape((n_components_show, h, w))
fig, axes = plt.subplots(2, 5, figsize=(15, 6))
for i, ax in enumerate(axes.flat):
if i < n_components_show:
ax.imshow(components[i], cmap='gray')
ax.set_title(f'Component {i+1}')
ax.axis('off')
plt.tight_layout()
plt.show()結(jié)論
本文探討了幾種用于數(shù)值數(shù)據(jù)的高級特征工程技術(shù),強調(diào)了它們在提高機器學(xué)習(xí)模型性能方面的關(guān)鍵作用。討論的方法包括:
- 歸一化
- 多項式特征
- FunctionTransformer
- KBinsDiscretizer
- 對數(shù)變換
- PowerTransformer (Box-Cox和Yeo-Johnson)
- QuantileTransformer
- PCA
每種技術(shù)都提供了特定的優(yōu)勢,適用于特定類型的數(shù)據(jù)和問題。最合適的變換選擇取決于數(shù)據(jù)的性質(zhì)、要解決的問題以及選擇的模型。沒有一種通用的解決方案,這使得實驗和驗證變得至關(guān)重要。