多維偏好分析（Multidimensional Preference Analysis, MPA）是一種在市場營銷、心理學(xué)和公共政策等領(lǐng)域廣泛應(yīng)用的分析工具，用于研究多維度下的復(fù)雜偏好決策過程。在高維數(shù)據(jù)集中，當(dāng)屬性與偏好之間存在非線性關(guān)系或維度重疊時(shí)，偏好的理解和可視化呈現(xiàn)出顯著的技術(shù)挑戰(zhàn)。

本文本將研究采用主成分分析（Principal Component Analysis, PCA）和K均值聚類算法對鳶尾花數(shù)據(jù)集進(jìn)行降維分析和模式識(shí)別。PCA用于數(shù)據(jù)降維的同時(shí)保持關(guān)鍵方差信息，聚類算法則用于探索數(shù)據(jù)的內(nèi)在分組特征。分析表明PCA能夠有效實(shí)現(xiàn)物種分類，在二維空間中保留95.8%的數(shù)據(jù)方差。K均值聚類識(shí)別出的模式與實(shí)際物種分類具有高度一致性，同時(shí)也反映出相近類別（如變色鳶尾和弗吉尼亞鳶尾）之間的重疊特征。

基于PCA和聚類分析的多維偏好分析方法為高維偏好數(shù)據(jù)的簡化和理解提供了可靠的分析框架。該方法能夠有效揭示數(shù)據(jù)中的隱含模式，對各領(lǐng)域的實(shí)際決策具有重要的應(yīng)用價(jià)值。

引言

消費(fèi)者行為研究中的一個(gè)核心問題是理解不同消費(fèi)群體的品牌偏好差異。例如某些消費(fèi)者偏好奢侈品牌，而另一些則更注重實(shí)用性；某款智能手機(jī)能獲得廣泛認(rèn)可，而具有相似技術(shù)參數(shù)的另一款卻未能引起市場共鳴。這種復(fù)雜的選擇行為很少由單一因素決定，而是多種因素共同作用的結(jié)果。多維偏好分析（MPA）[1-5]正是為解決這類復(fù)雜決策問題而開發(fā)的分析工具。

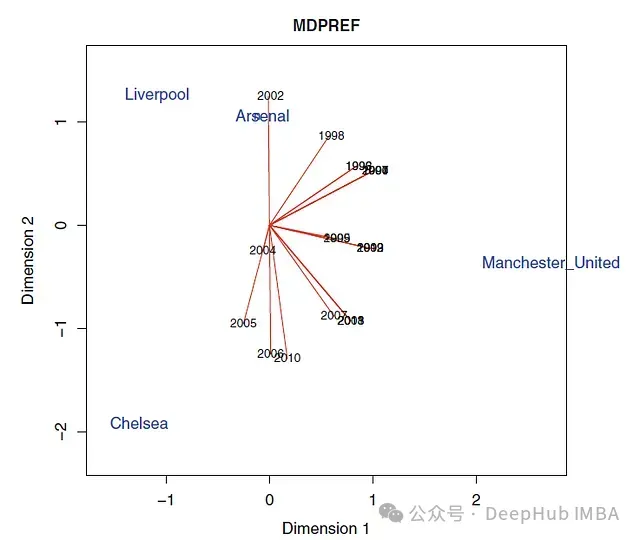
通過維度分析，我們可以將看似混沌的選擇行為轉(zhuǎn)化為可理解的模式。

偏好的多維特性分析

偏好決策很少呈現(xiàn)線性或單維特征。在實(shí)際情況中，個(gè)體和群體往往基于多個(gè)評(píng)價(jià)維度進(jìn)行選擇。以旅游目的地選擇為例，消費(fèi)者的決策過程涉及費(fèi)用、距離、氣候條件和活動(dòng)選項(xiàng)等多個(gè)維度的綜合權(quán)衡。多維偏好分析為研究者提供了一種系統(tǒng)方法，用于解析這些復(fù)雜的決策過程，深入理解不同屬性對決策的影響機(jī)制。

多維偏好分析主要探討兩個(gè)核心問題：

1. 識(shí)別決策過程中的關(guān)鍵影響因素
2. 分析這些因素之間的交互作用及其對偏好形成的影響機(jī)制

多維偏好分析通過主成分分析、多維尺度分析或聯(lián)合分析等統(tǒng)計(jì)方法，將抽象的偏好數(shù)據(jù)轉(zhuǎn)化為可量化的分析結(jié)果。這種方法不僅具有學(xué)術(shù)價(jià)值，還為市場營銷人員、政策制定者、產(chǎn)品設(shè)計(jì)師和人力資源管理者提供了實(shí)踐指導(dǎo)。

多維偏好分析的技術(shù)框架

多維偏好分析通常包含以下四個(gè)關(guān)鍵步驟：

數(shù)據(jù)采集：通過問卷調(diào)查、選擇實(shí)驗(yàn)或行為觀察收集偏好數(shù)據(jù)。例如，汽車制造商可能會(huì)要求消費(fèi)者對燃油效率、價(jià)格和外觀設(shè)計(jì)等因素進(jìn)行重要性評(píng)分。

維度降低：運(yùn)用統(tǒng)計(jì)模型將復(fù)雜的多屬性數(shù)據(jù)降維至可視化空間，以便發(fā)現(xiàn)數(shù)據(jù)中的潛在模式，如具有相似偏好特征的消費(fèi)者群體。

偏好映射：構(gòu)建感知圖譜，直觀展示產(chǎn)品屬性、消費(fèi)者偏好等要素之間的關(guān)系，為目標(biāo)市場定位提供依據(jù)。

分析應(yīng)用：基于多維偏好分析的結(jié)果指導(dǎo)決策，如產(chǎn)品改進(jìn)、營銷策略優(yōu)化或服務(wù)體系完善。

多維偏好分析的應(yīng)用領(lǐng)域

多維偏好分析在多個(gè)領(lǐng)域具有重要的應(yīng)用價(jià)值：

市場營銷與消費(fèi)者研究：通過分析客戶忠誠度和購買決策的影響因素，幫助企業(yè)優(yōu)化營銷策略。例如，零售商可以利用多維偏好分析在價(jià)格敏感性和品牌價(jià)值之間尋找平衡點(diǎn)。

公共政策制定：幫助政府部門評(píng)估社區(qū)需求優(yōu)先級(jí)，實(shí)現(xiàn)資源的優(yōu)化配置。

醫(yī)療衛(wèi)生服務(wù)：在以患者為中心的醫(yī)療實(shí)踐中，協(xié)助醫(yī)療人員綜合評(píng)估治療效果、經(jīng)濟(jì)成本和患者體驗(yàn)等多個(gè)維度。

人力資源管理：用于員工滿意度測評(píng)和福利體系設(shè)計(jì)，確保人力資源政策能夠滿足員工的多維需求。# 案例分析：智能手機(jī)市場的多維偏好研究

在一項(xiàng)針對智能手機(jī)市場的消費(fèi)者偏好研究中，研究者收集了消費(fèi)者對電池續(xù)航能力、攝像系統(tǒng)性能、價(jià)格水平和品牌價(jià)值等屬性的評(píng)價(jià)數(shù)據(jù)。通過多維偏好分析，研究發(fā)現(xiàn)消費(fèi)者可以劃分為兩個(gè)主要群體：一類消費(fèi)者更重視產(chǎn)品的技術(shù)創(chuàng)新性和品牌影響力，另一類則更關(guān)注性價(jià)比和基礎(chǔ)功能的可靠性。這些發(fā)現(xiàn)為制造商的產(chǎn)品線規(guī)劃和市場細(xì)分策略提供了重要參考，有助于提升市場份額和用戶滿意度。

實(shí)驗(yàn)研究

以下代碼展示了使用Iris數(shù)據(jù)集進(jìn)行多維偏好分析的具體實(shí)現(xiàn)過程，主要運(yùn)用了主成分分析和聚類分析方法。

import pandas as pd  
 import numpy as np  
 import seaborn as sns  
 import matplotlib.pyplot as plt  
 from sklearn.decomposition import PCA  
 from sklearn.preprocessing import StandardScaler  
 from sklearn.metrics import explained_variance_score  
 from sklearn.cluster import KMeans  
       
 # 導(dǎo)入Iris數(shù)據(jù)集  
 iris = sns.load_dataset('iris')  
       
 # 顯示數(shù)據(jù)樣本  
 print("Dataset Sample:")  
 print(iris.head())  
       
 # 特征和目標(biāo)變量分離  
 features = iris.drop(columns=['species'])  
 target = iris['species']  
       
 # 特征標(biāo)準(zhǔn)化處理  
 scaler = StandardScaler()  
 features_scaled = scaler.fit_transform(features)  
       
 # 執(zhí)行PCA降維，保留兩個(gè)主成分  
 pca = PCA(n_components=2)  
 principal_components = pca.fit_transform(features_scaled)  
       
 # 構(gòu)建包含PCA結(jié)果的數(shù)據(jù)框  
 pca_df = pd.DataFrame(data=principal_components, columns=['PC1', 'PC2'])  
 pca_df['species'] = target  
       
 # 計(jì)算解釋方差比  
 explained_variance = pca.explained_variance_ratio_  
 print("Explained Variance Ratio:", explained_variance)  
       
 # 應(yīng)用KMeans進(jìn)行聚類分析  
 kmeans = KMeans(n_clusters=3, random_state=42)  
 kmeans_labels = kmeans.fit_predict(principal_components)  
 pca_df['Cluster'] = kmeans_labels  
       
 # 計(jì)算解釋方差得分  
 variance_score = explained_variance_score(features_scaled, pca.inverse_transform(principal_components))  
 print("Explained Variance Score (Reconstruction):", variance_score)  
       
 # 繪制PCA結(jié)果和聚類結(jié)果  
 plt.figure(figsize=(12, 6))  
 plt.subplot(1, 2, 1)  
 sns.scatterplot(x='PC1', y='PC2', hue='species', data=pca_df, palette='deep')  
 plt.title('PCA: Iris Species')  
 plt.xlabel('Principal Component 1')  
 plt.ylabel('Principal Component 2')  
       
 plt.subplot(1, 2, 2)  
 sns.scatterplot(x='PC1', y='PC2', hue='Cluster', data=pca_df, palette='viridis')  
 plt.title('PCA: KMeans Clusters')  
 plt.xlabel('Principal Component 1')  
 plt.ylabel('Principal Component 2')  
 plt.tight_layout()  
 plt.show()  
       
 # 結(jié)果分析  
 print("\nInterpretation:")  
 print(f"PCA reduced the dataset from 4 dimensions to 2 while retaining {sum(explained_variance) * 100:.2f}% of the variance.")  
 print("The scatter plot shows that PCA effectively separates the species in the Iris dataset.")  
 print("KMeans clustering also highlights separability, though some overlap is observed.")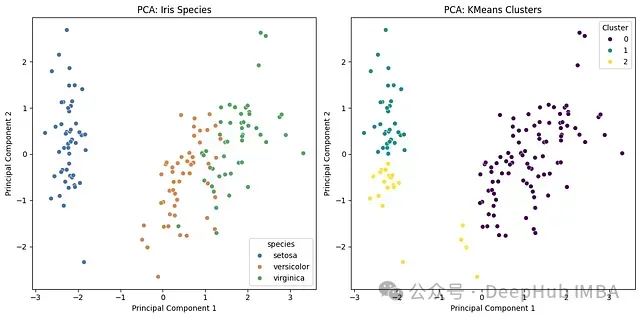

實(shí)驗(yàn)結(jié)果闡明了多維數(shù)據(jù)分析中的關(guān)鍵技術(shù)路徑，展示了PCA在數(shù)據(jù)降維和模式識(shí)別中的應(yīng)用價(jià)值。

基于物種的PCA分析結(jié)果

物種分類效果：PCA投影顯著區(qū)分了鳶尾花數(shù)據(jù)集中的三個(gè)物種（setosa、versicolor、virginica）。

山鳶尾特征：在第一主成分方向上，山鳶尾與其他兩個(gè)物種形成明顯分離。

變色鳶尾和弗吉尼亞鳶尾的特征重疊：這兩個(gè)物種在特征空間中表現(xiàn)出部分重疊，說明它們具有相似的形態(tài)特征。

方差解釋能力：前兩個(gè)主成分保留了數(shù)據(jù)集的主要信息，為進(jìn)一步分析提供了可靠的簡化表示。

基于K均值的聚類分析結(jié)果

聚類效果：K均值算法將降維后的數(shù)據(jù)劃分為三個(gè)群組。

*分類準(zhǔn)確性**：聚類結(jié)果與物種分類具有較高的一致性，尤其是山鳶尾類別表現(xiàn)出良好的可分性。

邊界模糊性：在變色鳶尾和弗吉尼亞鳶尾之間存在一定的分類誤差，這反映了它們在特征空間中的自然重疊現(xiàn)象。

無監(jiān)督學(xué)習(xí)效果：K均值聚類在沒有先驗(yàn)標(biāo)簽信息的情況下，能夠較好地識(shí)別數(shù)據(jù)集中的自然分組結(jié)構(gòu)。

主要研究發(fā)現(xiàn)

降維效果：PCA算法成功將四維數(shù)據(jù)降至二維表示，同時(shí)保持了數(shù)據(jù)的主要變異信息，為數(shù)據(jù)可視化和分析提供了有效途徑。

聚類效果：K均值聚類在無監(jiān)督學(xué)習(xí)條件下，識(shí)別出的模式與實(shí)際物種分類高度吻合，驗(yàn)證了該方法在探索性數(shù)據(jù)分析中的實(shí)用價(jià)值。

應(yīng)用價(jià)值：本研究采用的分析方法可推廣應(yīng)用于客戶偏好分析、數(shù)據(jù)分類以及多維數(shù)據(jù)集的結(jié)構(gòu)探索等實(shí)際問題。

總結(jié)

多維偏好分析為復(fù)雜決策問題提供了系統(tǒng)的分析框架，能夠?qū)⒊橄蟮闹饔^數(shù)據(jù)轉(zhuǎn)化為可量化的分析結(jié)果。無論是在市場營銷策略制定、新產(chǎn)品開發(fā)還是資源配置決策中，多維偏好分析都能為決策者提供有價(jià)值的數(shù)據(jù)支持。通過這種系統(tǒng)化的分析方法，組織能夠更好地理解目標(biāo)群體的需求特征，從而制定更有針對性的決策方案。

研究表明，復(fù)雜決策問題的核心在于理解和把握影響決策的關(guān)鍵維度。這不僅需要收集全面的數(shù)據(jù)，更需要采用適當(dāng)?shù)姆治龇椒▉斫沂緮?shù)據(jù)中的深層模式。

針對多維偏好分析在實(shí)際應(yīng)用中遇到的技術(shù)難點(diǎn)，未來研究可以從以下幾個(gè)方面展開：

1. 開發(fā)更高效的降維算法
2. 提升聚類方法在處理重疊數(shù)據(jù)時(shí)的準(zhǔn)確性
3. 探索新的可視化方法以更好地展示高維數(shù)據(jù)的特征