在機器學習的領域中，我們對原始數據進行特征提取，經常會得到高維度的特征向量。在這些多特征的高維空間中，會包含一些冗余和噪聲。所以我們希望通過降維的方式來尋找數據內部的特性，提升特征表達能力，降低模型的訓練成本。PCA是一種降維的經典算法，屬于線性、非監督、全局的降維方法。

一、PCA原理

PCA的原理是線性映射，簡單的說就是將高維空間數據投影到低維空間上，然后將數據包含信息量大的主成分保留下來，忽略掉對數據描述不重要的次要信息。而對于正交屬性空間中的樣本，如何用一個超平面對所有樣本進行恰當合適的表達呢?若存在這樣的超平面，應該具有兩種性質：

• 所有樣本點到超平面的距離最近
• 樣本點在這個超平面的投影盡可能分開

以上兩種性質便是主成分分析的兩種等價的推導，即PCA最小平方誤差理論和PCA最大方差理論，本篇主要為大家介紹最大方差理論。 PCA的降維操作是選取數據離散程度最大的方向(方差最大的方向)作為第一主成分，第二主成分選擇方差次大的方向，并且與第一個主成分正交。不算重復這個過程直到找到k個主成分。

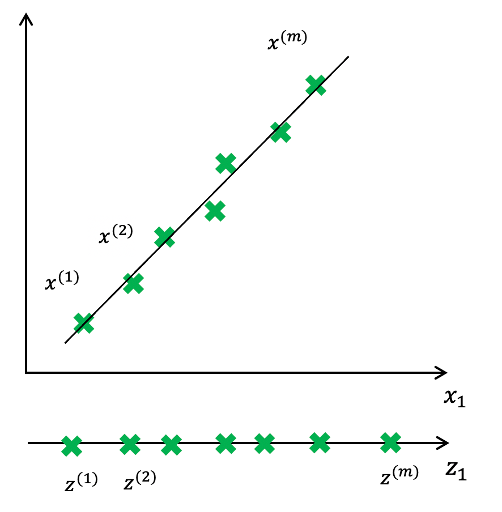
數據點分布在主成分方向上的離散程度最大，且主成分向量彼此之間正交。

二、PCA算法實現步驟

1、對所有數據特征進行中心化和歸一化對樣本進行平移使其重心在原點，并且消除不同特征數值大小的影響，轉換為統一量綱：

2、計算樣本的協方差矩陣

協方差是對兩個隨機變量聯合分布線性相關程度的一種度量;

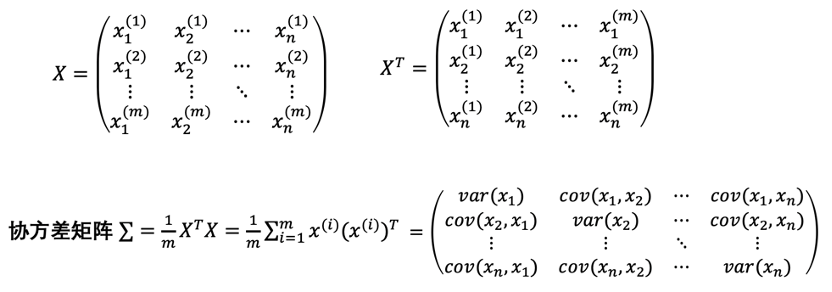
3、對協方差矩陣求解特征值和特征向量

注意點：1、對稱矩陣的特征向量相互正交，其點乘為02、數據點在特征向量上投影的方差，為對應的特征值，選擇特征值大的特征向量，就是選擇點投影方差大的方向，即是具有高信息量的主成分;次佳投影方向位于最佳投影方向的正交空間，是第二大特征值對應的特征向量，以此類推; 4、選取k個最大大特征值對應的特征向量，即是k個主成分 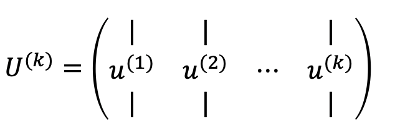U是協方差矩陣所有的特征向量構成的矩陣，對應的特征值滿足：λ1>λ2>?>λn，同時使其滿足在主成分向量上投影的方差和占總方差的99%或者95%以上，即確定了k的選取。

三、降維python實現

1、配置環境，導入相關包

2、讀取數據

3、讀取特征、標簽列，并進行中心化歸一化，選取主成分個數，前2個主成分的方差和>95%

4、將降維后特征可視化，橫縱坐標代表兩個主成分，顏色代表結果標簽分類，即可根據主成分進行后續分析、建模

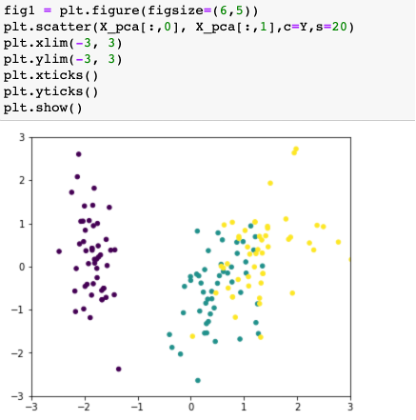
以上PCA主成分分析就講完了，本文進行了樣本點在超平面的投影盡可能分開的推導原理闡述，大家感興趣的可以研究另一種等價推導，即樣本點到超平面的距離最近。