巧妙應用機器學習引導科研理解
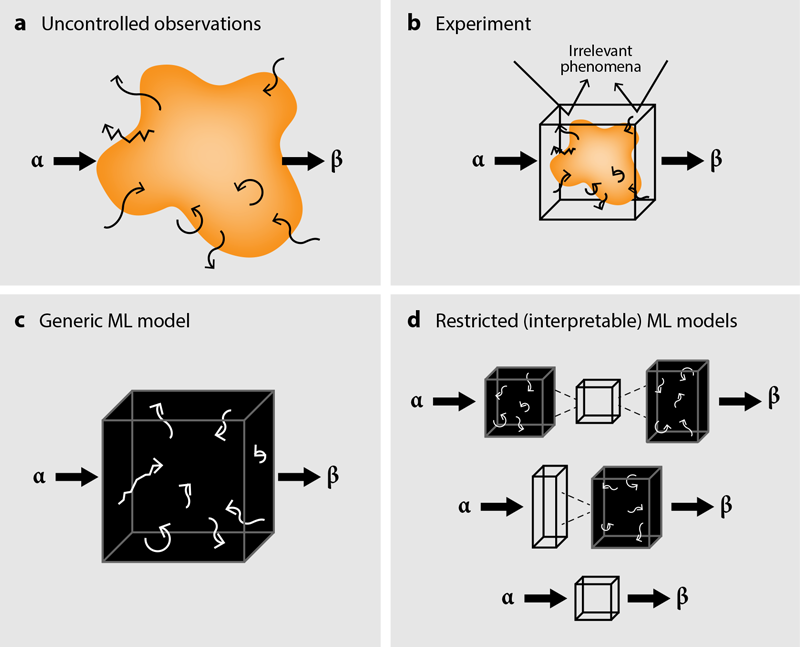
圖1:理解物理現象的途徑有很多,其中原因α產生結果β。(a) 不受控制的觀察會導致原因和結果之間的松散聯系。(b) 結合已知物理定律的精心設計的實驗可以得到簡單的因果關系,但為復雜現象設計這樣的實驗可能極具挑戰性。(c) 通用的機器學習(ML)模型(神經網絡)通過優化許多參數來擬合復雜數據,但解析這些黑箱(例如,數百萬個)參數的意義是非常困難的。(d) 包含一些限制或簡化操作(白色)的機器學習模型使得識別復雜現象的因果鏈的某些方面成為可能,從而指導模型構建或進一步實驗。
物理理論和機器學習(ML)模型都依賴于其在未見情境下預測結果的能力。然而,對于前者的要求要高得多。要成為被接受的知識,理論必須符合已知的物理定律——而且,至關重要的是,必須是可解釋的。
一個可解釋的理論能夠解釋現象為何發生,而不僅僅是預測其形式。擁有這樣的解釋可以指導新理論的范圍,使其能夠在新的背景下應用,同時也將其與先前的知識聯系起來并納入其中。
迄今為止,研究人員在使ML模型(或任何自動化優化過程)產生符合這些標準的新理論方面仍然存在很大困難。
芝加哥大學的喬納森·科倫和文琴佐·維泰利及其同事現在展示了成功地利用ML的方式——不是作為研究人員的替代者,而是作為指導者,幫助構建復雜系統的模型[1]。在他們方法的演示中,研究人員發現了一個先前被忽視的項,推進了對流體系統動力學的更全面理解。
為了建立新模型,物理學家通常在受控實驗中觀察現象(圖1a),并嘗試用方程將系統的參數相互關聯(圖1b)。然后,通過直覺和試錯的組合,物理學家們修改實驗、理論或兩者同時修改,直到找到一組描述數據的方程。
先前的知識——例如,系統應該沒有歷史依賴,溫度是均勻的,或忽略重力——大大縮小了可能的解決方案和所需實驗探索的范圍。這種范圍的大幅度縮小通常是必要的,因為我們發現人類很難處理超過屈指可數幾個維度的問題。
相比之下,ML模型在給定(非常)高維空間進行探索時能找到更準確且更具普遍性的解決方案[2]。這些模型優化大量可調參數,直到其預測與數據匹配。不幸的是,通用ML模型找到的解決方案通常過于復雜且方法依賴性強,難以提取“為什么”[3]。
因此,應用這些方法的研究人員往往局限于不能令人滿意的說法,即他們的數據包含預測信息[4]。然而,這些信息是什么以及為什么具有預測性,仍然隱藏在眾多雜亂變量的黑箱中(圖1c)。
識別數據中預測信息所在的技術正在出現[5],但在科學過程中很少使用。復雜ML模型的替代方案是使用算法直接搜索可能方程的庫來描述系統[6]。
然而,這種策略隨著系統復雜性的增加而效果不佳,使其在現在科研關注的現象中難以應用。將ML融入一般發現過程中需要平衡:方法應具有足夠的自由度以發揮其潛力,同時結果所在的領域也應受到限制,以便結果可解釋。
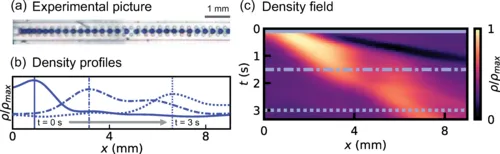
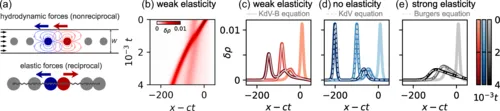
科倫、維泰利及其同事正是通過一系列ML算法實現了這一點[1]。他們的工作集中在流體力學中的一個范例問題上:微流體通道中水滴的單排隊列,懸浮在另一種流體中,這使它們相互作用并形成傳播的沖擊前沿。該系統以前通過一個描述流體密度變化的偏微分方程建模。
但這個方程(稱為伯格斯方程),未能捕捉系統動力學的關鍵方面。為了揭示缺失的物理學,研究人員首先訓練一個ML模型來預測一維水滴密度場ρ的時間演變——換句話說,他們讓算法找到一個函數M,使初始密度ρ0隨時間演進:M[t,ρ0]=ρ(t)。
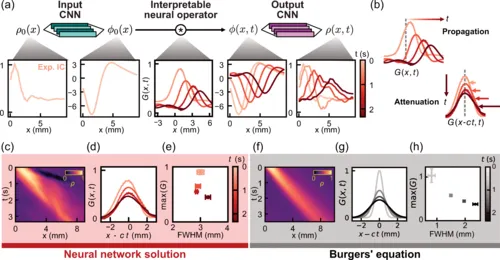
為了使他們的模型具有可解釋性,研究人員將其構建為三個連續操作的組合。
首先,一個神經網絡 N 將密度轉換為一個新的1D場,他們稱之為 φ0=N[ρ0]。雖然這個“潛在”場沒有容易解釋的物理意義,它僅包含有關初始密度場的信息。
其次,將這個場輸入到一個稱為 F 的函數中,該函數使其隨時間推進——換句話說,F(φ0,t)=φ(t)。研究人員將 F 的形式限制為一組線性操作。
最后,這個場通過另一個神經網絡轉換回密度,基本上是第一個步驟的逆過程。(從數學上講,整個過程可以描述為 M[t,ρ0]=N?1[F(t,N[ρ0])]=ρ(t) ,如圖1d上方所示)。通過同時優化這三個步驟以匹配實驗數據,研究人員發現比伯格斯方程更好的預測結果。
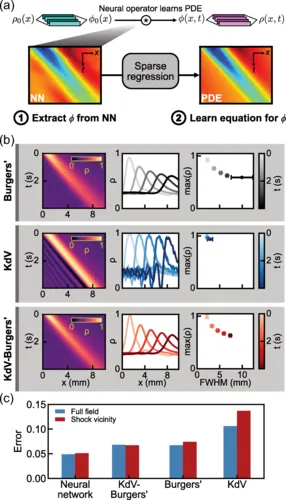
隨后,研究人員利用一種算法來尋找數值函數的簡化分析逼近[6]。對于一個在實驗數據上訓練的典型的神經網絡,這一步驟通常會失敗(圖1c)。
但值得注意的是,它產生了一個包含五個項的線性偏微分方程,作為 F 的良好替代。盡管這個方程作用于(不可解釋的)潛在變量 φ0,但 F 作為時間傳播者的角色使得每一項的意義在高層次上是可以理解的。
具體來說,研究人員將其中一個微分項與色散相關聯——即流體波速的頻率依賴性。這樣的色散項在伯格斯方程中并不存在,但團隊發現其加入能更準確地描述水滴密度場中出現的沖擊前沿動力學。
最后,團隊開發了一個相互作用水滴的模型,發現這個新增的色散項是非對稱流體動力學相互作用的直接結果。
這項工作提供了一個令人興奮的機器學習(ML)應用,它在科學探索中充當了羅盤,這需要一種根本不同于標準ML實踐的方法,后者主要通過預測準確性來評判模型。然而,對于科學探索來說,“最佳”模型是那些能夠提供物理洞察(即“為什么”)的模型,即使它們可能不是最準確的。
事實上,團隊發現添加關鍵的色散項實際使預測誤差略微增加,相比之下,其他ML模型在相同問題上的應用誤差較低;然而,這一色散項清楚地捕捉了沖擊前沿附近缺失的物理現象。正是通過連續模型的閉環并識別這一色散項的來源,科倫、維泰利及其同事才能鞏固他們的結論。
這一工作流程與賓夕法尼亞大學近期使用ML作為實驗指南的工作相呼應[7],在這些工作中,訓練預測顆粒材料堵塞的最簡單和“最弱”(最不具預測性)的模型提供了最深刻的見解,并提升實驗驗證了他們的解釋。
計算能力的提升極大地加快了科學數據分析,但我們對這些數據的探索通常仍完全由人類驅動。隨著物理學家研究日益復雜的涌現現象,潛在物理模型的維度、以及所需實驗探索的復雜性迅速增長。
雖然標準分析工具允許我們識別可靠的趨勢,但在(必然)雜亂的數據中追蹤高度非線性、歷史依賴和多尺度效應可能不切實際,除非有一個能夠同時處理100維數據的指南。研究這些現象,可能需要對學科內容和ML工具的熟練掌握,這既可以作為實驗指導,也可以作為理論指導。
參考文獻
- J. Colen et al., “Interpreting neural operators: How nonlinear waves propagate in nonreciprocal solids,”Phys. Rev. Lett. 133, 107301 (2024).
- J. W. Rocks and P. Mehta, “Memorizing without overfitting: Bias, variance, and interpolation in overparameterized models,”Phys. Rev. Res. 4, 013201 (2022).
- C. Rudin et al., “Interpretable machine learning: Fundamental principles and 10 grand challenges,”Statist. Surv. 16, 1 (2022).
- S. Dillavou et al., “Beyond quality and quantity: Spatial distribution of contact encodes frictional strength,”Phys. Rev. E 106, 033001 (2022).
- K. A. Murphy and D. S. Bassett, “Information decomposition in complex systems via machine learning,”Proc. Natl. Acad. Sci. U.S.A. 121, 13 (2024).
- S. L. Brunton et al., “Discovering governing equations from data by sparse identification of nonlinear dynamical systems,”Proc. Natl. Acad. Sci. U.S.A. 113, 3932 (2016).
- J. M. Hanlan et al., “Cornerstones are the key stones: Using interpretable machine learning to probe the clogging process in 2D granular hoppers,”arXiv:2407.05491.

















