在之前談到的保序回歸加速話題中，我們聊起如何利用Cython改進回歸算法的性能表現。我覺得將Python優化代碼的性能表現與原生Julia方案加以比對能夠進一步明確大家對于速度提升的直觀感受。

今天的文章將承接上一篇，因此大家在進行閱讀前，不妨先對前文進行一番回顧、旨在掌握相關背景信息。

我們將借用前文中提到的兩種算法，并在這里就性能表現在Julia與Python之間展開一番比拼。

線性PAVA

相關Cython代碼可以通過Github上的scikit-learn進行下載，而Julia代碼則來自GitHub上的Isotonic.jl。

Julia代碼采用的是最為簡單的PAVA表達，不摻雜任何花哨的內容與修飾；@inbounds宏的作用是客觀比較Cython的執行效果并關閉bound check。

function isotonic_regression(y::Vector{Float64}, weights::Vector{Float64})  
    @inbounds begin  
        n = size(y, 1)  
        if n <= 1 
            return y  
        end  
        n -= 1 
        while true  
            i = 1 
            pooled = 0 
            while i <= n  
                k = i  
                while k <= n && y[k] >= y[k+1]  
                    k += 1 
                end  
   
                # Find a decreasing subsequence, and update  
                # all points in the sequence to the weighted average.  
                if y[i] != y[k]  
                    numerator = 0.0 
                    denominator = 0.0 
                    for j in i : k  
                        numerator += y[j] * weights[j]  
                        denominator += weights[j]  
                    end  
   
                    for j in i : k  
                        y[j] = numerator / denominator  
                    end  
                    pooled = 1 
                end  
                i = k + 1 
            end  
            if pooled == 0 
                break 
            end  
        end  
    end  
    return y  
end  
   
isotonic_regression(y::Vector{Float64}) = isotonic_regression(y, ones(size(y, 1)))  

linear_pava.jl hosted with ❤ by GitHub

@cython.boundscheck(False)  
@cython.wraparound(False)  
@cython.cdivision(True)  
def _isotonic_regression(np.ndarray[DOUBLE, ndim=1] y,  
                         np.ndarray[DOUBLE, ndim=1] weight,  
                         np.ndarray[DOUBLE, ndim=1] solution):  
    cdef:  
        DOUBLE numerator, denominator  
        Py_ssize_t i, pooled, n, k  
   
    n = y.shape[0]  
    # The algorithm proceeds by iteratively updating the solution  
    # array.  
   
    # TODO - should we just pass in a pre-copied solution  
    # array and mutate that?  
    for i in range(n):  
        solution[i] = y[i]  
   
    if n <= 1:  
        return solution  
   
    n -= 1 
    while 1:  
        # repeat until there are no more adjacent violators.  
        i = 0 
        pooled = 0 
        while i < n: 
            k = i 
            while k < n and solution[k] >= solution[k + 1]:  
                k += 1  
            if solution[i] != solution[k]:  
                # solution[i:k + 1] is a decreasing subsequence, so  
                # replace each point in the subsequence with the  
                # weighted average of the subsequence.  
   
                # TODO: explore replacing each subsequence with a  
                # _single_ weighted point, and reconstruct the whole  
                # sequence from the sequence of collapsed points.  
                # Theoretically should reduce running time, though  
                # initial experiments weren't promising.  
                numerator = 0.0  
                denominator = 0.0  
                for j in range(i, k + 1):  
                    numerator += solution[j] * weight[j]  
                    denominator += weight[j]  
                for j in range(i, k + 1):  
                    solution[j] = numerator / denominator  
                pooled = 1 
            i = k + 1  
        # Check for convergence  
        if pooled == 0:  
            break  
   
    return solution  

_isotonic.pyx hosted with ❤ by GitHub

Active Set

Active Set的行數與Cython代碼基本相當，而且在結構上可能更為簡潔（通過顯式復合type ActiveState實現）、旨在維持給定主動雙重變量中的參數。Active Set會將重復代碼拆分為獨立函數，從而由LLVM對其實現內聯——這一點很難借由Cython中的任何參數實現。

Julia中的檢索機制也會對算法作出一定程度的精簡。

immutable ActiveState  
    weighted_label::Float64  
    weight::Float64  
    lower::Int64  
    upper::Int64  
   
end  
   
function merge_state(l::ActiveState, r::ActiveState)  
    return ActiveState(l.weighted_label + r.weighted_label,  
                       l.weight + r.weight,  
                       l.lower,  
                       r.upper)  
end  
   
function below(l::ActiveState, r::ActiveState)  
    return l.weighted_label * r.weight <= l.weight * r.weighted_label  
end  
   
function active_set_isotonic_regression(y::Vector{Float64}, weights::Vector{Float64})  
    @inbounds begin  
        active_set = [ActiveState(weights[i] * y[i], weights[i], i, i) for i in 1 : size(y, 1)]  
        current = 1 
        while current < size(active_set, 1)  
            while current < size(active_set, 1) && below(active_set[current], active_set[current+1])  
                current += 1 
            end  
            if current == size(active_set, 1)  
                break 
            end  
   
            merged = merge_state(active_set[current], active_set[current+1])  
            splice!(active_set, current:current+1, [merged])  
            while current > 1 && !below(active_set[current-1], active_set[current])  
                current -= 1 
                merged = merge_state(active_set[current], active_set[current+1])  
                splice!(active_set, current:current+1, [merged])  
            end  
        end  
   
        for as in active_set  
            y[as.lower:as.upper] = as.weighted_label / as.weight  
        end  
    end  
    return y  
end  
   
active_set_isotonic_regression(y::Vector{Float64}) = active_set_isotonic_regression(y, ones(size(y, 1)))  

active_set.jl hosted with ❤ by GitHub

@cython.boundscheck(False)  
@cython.wraparound(False)  
@cython.cdivision(True)  
def _isotonic_regression(np.ndarray[DOUBLE, ndim=1] y,  
                         np.ndarray[DOUBLE, ndim=1] weight,  
                         np.ndarray[DOUBLE, ndim=1] solution):  
   
    cdef:  
        Py_ssize_t current, i  
        unsigned int len_active_set  
        DOUBLE v, w  
   
    len_active_set = y.shape[0]  
    active_set = [[weight[i] * y[i], weight[i], [i, ]]  
                  for i in range(len_active_set)]  
    current = 0 
   
    while current < len_active_set - 1:  
        while current < len_active_set -1 and \  
              (active_set[current][0] * active_set[current + 1][1] <=   
               active_set[current][1] * active_set[current + 1][0]):  
            current += 1 
   
        if current == len_active_set - 1:  
            break 
   
        # merge two groups  
        active_set[current][0] += active_set[current + 1][0]  
        active_set[current][1] += active_set[current + 1][1]  
        active_set[current][2] += active_set[current + 1][2]  
   
        active_set.pop(current + 1)  
        len_active_set -= 1 
        while current > 0 and \  
              (active_set[current - 1][0] * active_set[current][1] >   
               active_set[current - 1][1] * active_set[current][0]):  
            current -= 1 
            active_set[current][0] += active_set[current + 1][0]  
            active_set[current][1] += active_set[current + 1][1]  
            active_set[current][2] += active_set[current + 1][2]  
   
            active_set.pop(current + 1)  
            len_active_set -= 1 
   
    for v, w, idx in active_set:  
        solution[idx] = v / w  
    return solution  

_isotonic.pyx hosted with ❤ by GitHub 

性能表現

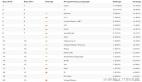
可以看到，在與Cython實例進行比對時，我們發現即使是同樣的算法在Julia中的平均執行速度也會更快。

[點擊擴大]

對于上述Active Set實例，Julia在處理回歸計算時的表現都能實現5倍到300倍的速度提升。

對于線性PAVA實例，Julia的速度提升效果則為1.1倍到4倍之間。

這樣的結果證明，Julia在性能敏感型機器學習應用領域具有顯著吸引力。

大家可以點擊此處了解更多關于上述性能測試結果的獲取方法。

英文原文：http://tullo.ch/articles/python-vs-julia/