“小數據”的統計學
一、小數據來自哪里?
科技公司的數據科學、關聯性分析以及機器學習等方面的活動大多圍繞著”大數據”,這些大型數據集包含文檔、 用戶、 文件、 查詢、 歌曲、 圖片等信息,規模數以千計,數十萬、 數百萬、 甚至數十億。過去十年里,處理這類型數據集的基礎設施、 工具和算法發展得非常迅速,并且得到了不斷改善。大多數數據科學家和機器學習從業人員就是在這樣的情況下積累了經驗,逐漸習慣于那些用著順手的算法,而且在那些常見的需要權衡的問題上面擁有良好的直覺(經常需要權衡的問題包括:偏差和方差,靈活性和穩定性,手工特性提取和特征學習等等)。但小的數據集仍然時不時的出現,而且伴隨的問題往往難以處理,需要一組不同的算法和不同的技能。小數據集出現在以下幾種情況:
- 企業解決方案: 當您嘗試為一個人員數量相對有限的企業提供解決方案,而不是為成千上萬的用戶提供單一的解決方案。
- 時間序列: 時間供不應求!尤其是和用戶、查詢指令、會話、文件等相比較。這顯然取決于時間單位或采樣率,但是想每次都能有效地增加采樣率沒那么容易,比如你得到的標定數據是日期的話,那么你每天只有一個數據點。
- 關于以下樣本的聚類模型:州市、國家、運動隊或任何總體本身是有限的情況(或者采樣真的很貴)。【備注:比如對美國50個州做聚類】
- 多變量 A/B 測試: 實驗方法或者它們的組合會成為數據點。如果你正在考慮3個維度,每個維度設置4個配置項,那么將擁有12個點。【備注:比如在網頁測試中,選擇字體顏色、字體大小、字體類型三個維度,然后有四種顏色、四個字號、四個字型】
- 任何罕見現象的模型,例如地震、洪水。
二、小數據問題
小數據問題很多,但主要圍繞高方差:
- 很難避免過度擬合
- 你不只過度擬合訓練數據,有時還過度擬合驗證數據。
- 離群值(異常點)變得更危險。
- 通常,噪聲是個現實問題,存在于目標變量中或在一些特征中。
三、如何處理以下情況
1-雇一個統計學家
我不是在開玩笑!統計學家是原始的數據科學家。當數據更難獲取時統計學誕生了,因而統計學家非常清楚如何處理小樣本問題。統計檢驗、參數模型、自舉法(Bootstrapping,一種重復抽樣技術),和其他有用的數學工具屬于經典統計的范疇,而不是現代機器學習。如果沒有好的專業統計員,您可以雇一個海洋生物學家、動物學家、心理學家或任何一個接受過小樣本處理訓練的人。當然,他們的專業履歷越接近您的領域越好。如果您不想雇一個全職統計員,那么可以請臨時顧問。但雇一個科班出身的統計學家可能是非常好的投資。
2-堅持簡單模型
更確切地說: 堅持一組有限的假設。預測建模可以看成一個搜索問題。從初始的一批可能模型中,選出那個最適合我們數據的模型。在某種程度上,每一個我們用來擬合的點會投票,給不傾向于產生這個點的模型投反對票,給傾向于產生這個點的模型投贊成票。當你有一大堆數據時,你能有效地在一大堆模型/假設中搜尋,最終找到適合的那個。當你一開始沒有那么多的數據點時,你需要從一套相當小的可能的假設開始 (例如,含有 3個非零權重的線性模型,深度小于4的決策樹模型,含有十個等間隔容器的直方圖)。這意味著你排除復雜的設想,比如說那些非線性或特征之間相互作用的問題。這也意味著,你不能用太多自由度 (太多的權重或參數)擬合模型。適當時,請使用強假設 (例如,非負權重,沒有交互作用的特征,特定分布等等) 來縮小可能的假設的范圍。
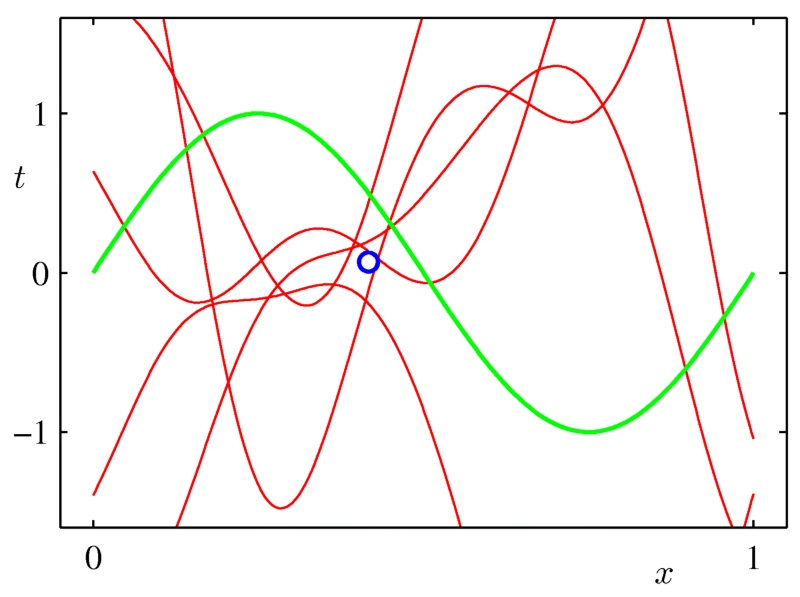
任何瘋狂的模型都能擬合單點。
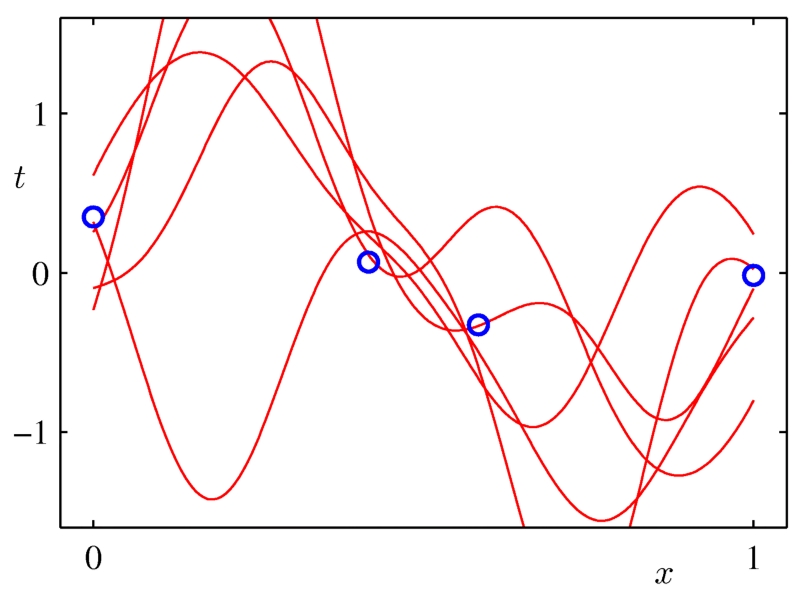
當我們有更多的數據點時,越來越少的模型可以擬合這些點。
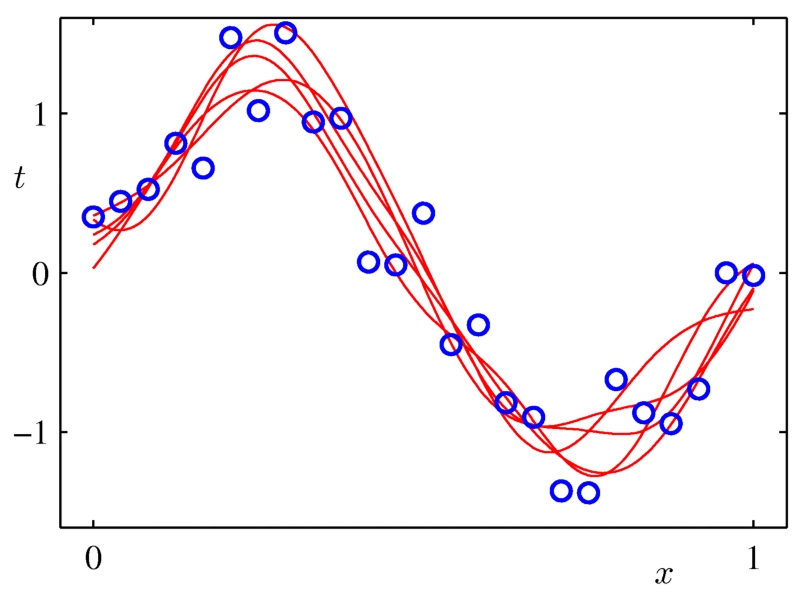
圖像來自Chris Bishop的書《模式識別和機器學習》
3-盡可能使用更多的數據
您想構建一個個性化的垃圾郵件過濾器嗎?嘗試構建在一個通用模型,并為所有用戶訓練這個模型。你正在為某一個國家的GDP建模嗎?嘗試用你的模型去擬合所有能得到數據的國家,或許可以用重要性抽樣來強調你感興趣的國家。你試圖預測特定的火山爆發嗎?……你應該知道如何做了。
4-做試驗要克制
不要過分使用驗證集。如果你嘗試過許多不同的技術,并使用一個保留數據集來對比它們,那么你應該清楚這些結果的統計效力如何,而且要意識到對于樣本以外的數據它可能不是一個好的模型。
5-清洗您的數據
處理小數據集時,噪聲和異常點都特別煩人。為了得到更好的模型,清洗您的數據可能是至關重要的。或者您可以使用魯棒性更好的模型,尤其針對異常點。(例如分位數回歸)
6-進行特征選擇
我不是顯式特征選擇的超級粉絲。我通常選擇用正則化和模型平均 (下面會展開講述)來防止過度擬合。但是,如果數據真的很少,有時顯式特征選擇至關重要。可以的話,***借助某一領域的專業知識來做特征選擇或刪減,因為窮舉法 (例如所有子集或貪婪前向選擇) 一樣容易造成過度擬合。
7-使用正則化
對于防止模型過擬合,且在不降低模型中參數實際數目的前提下減少有效自由度,正則化幾乎是神奇的解決辦法。L1正則化用較少的非零參數構建模型,有效地執行隱式特征選擇。而 L2 正則化用更保守 (接近零) 的參數,相當于有效的得到了強零中心的先驗參數 (貝葉斯理論)。通常,L2 擁有比L1更好的預測精度。【備注:L2正則化的效果使權重衰減,人們普遍認為:更小的權值從某種意義上說,表示網絡的復雜度更低,對數據的擬合剛剛好,這個法則也叫做奧卡姆剃刀。】
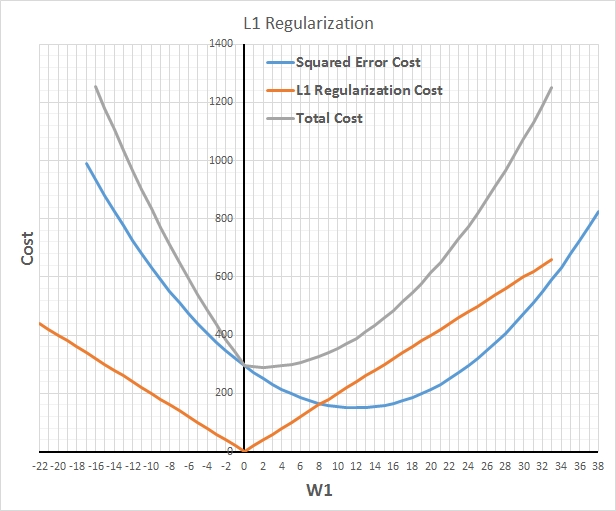
L1正則化可以使得大多數參數變為零
8 使用模型平均
模型平均擁有類似正則化的效果,它減少方差,提高泛化,但它是一個通用的技術,可以在任何類型的模型上甚至在異構模型的集合上使用。缺點是,為了做模型平均,結果要處理一堆模型,模型的評估變得很慢。bagging和貝葉斯模型平均是兩個好用的模型平均方法。
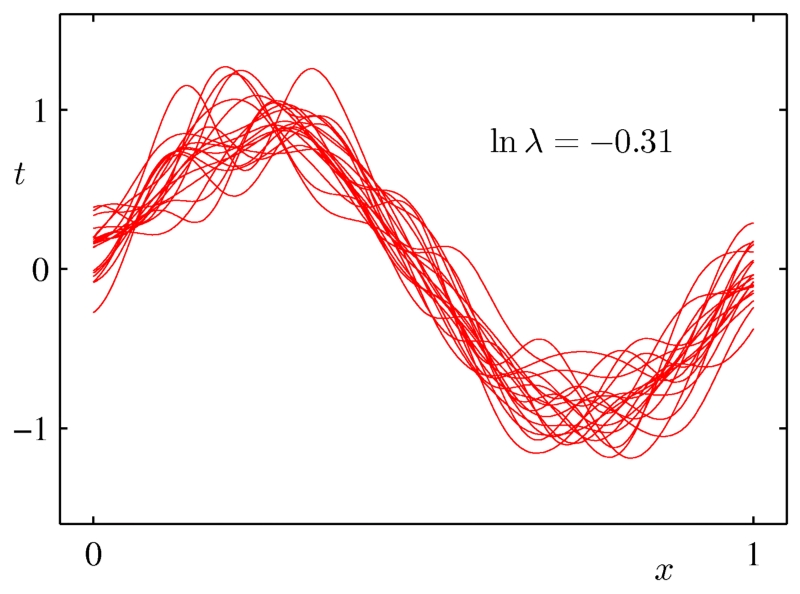
每條紅線是一個擬合模型。
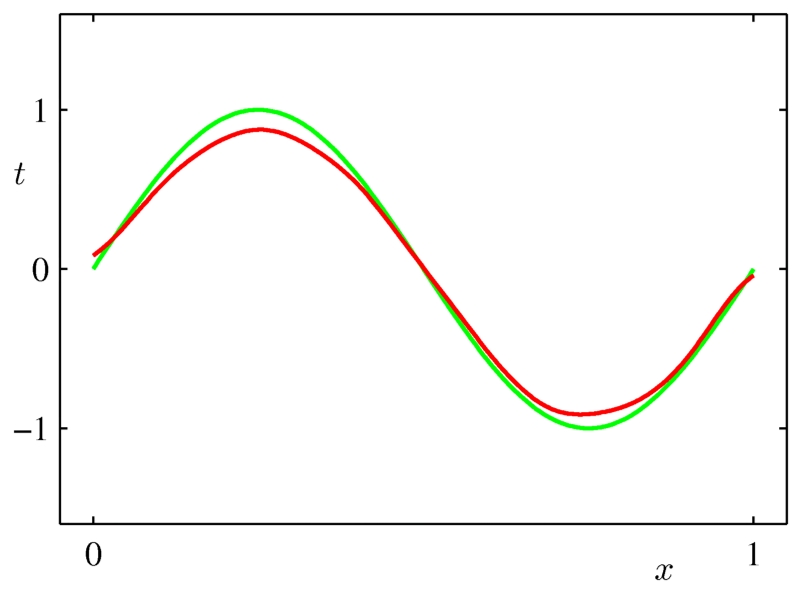
平均這些高方差模型之后,我們得到一個平滑的曲線,它很好的擬合了原有數據點的分布。
9-嘗試貝葉斯建模和模型平均
這個依然不是我喜歡的技術,但貝葉斯推理可能適合于處理較小的數據集,尤其是當你能夠使用專業知識構造好的先驗參數時。
10-喜歡用置信區間
通常,除了構建一個預測模型之外,估計這個模型的置信是個好主意。對于回歸分析,它通常是一個以點估計值為中心的取值范圍,真實值以95%的置信水平落在這個區間里。如果是分類模型的話,那么涉及的將是分類的概率。這種估計對于小數據集更加重要,因為很有可能模型的某些特征相比其它特征沒有更好的表達出來。如上所述的模型平均允許我們很容易得到在回歸、 分類和密度估計中做置信的一般方法。當評估您的模型時它也很有用。使用置信區間評估模型性能將助于你避免得出很多錯誤的結論。
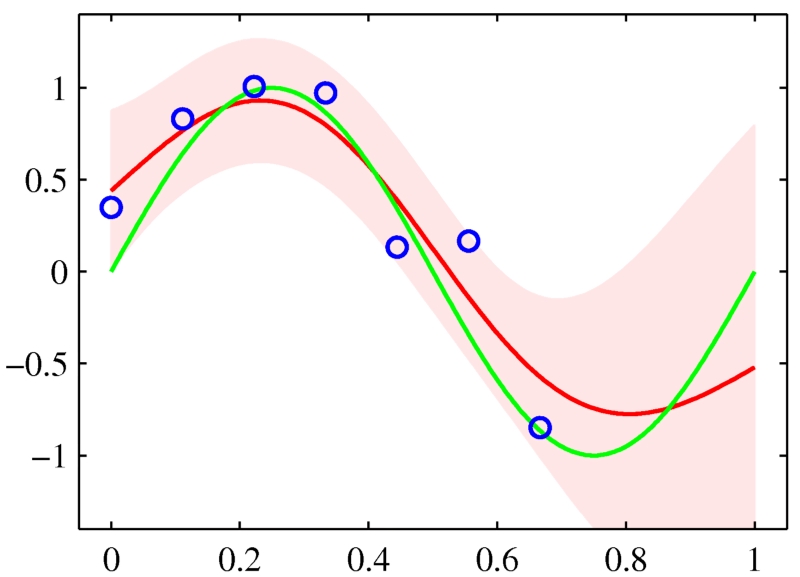
你的數據不樂意出現在特征空間的某些區域,那么預測置信應該有所反應。
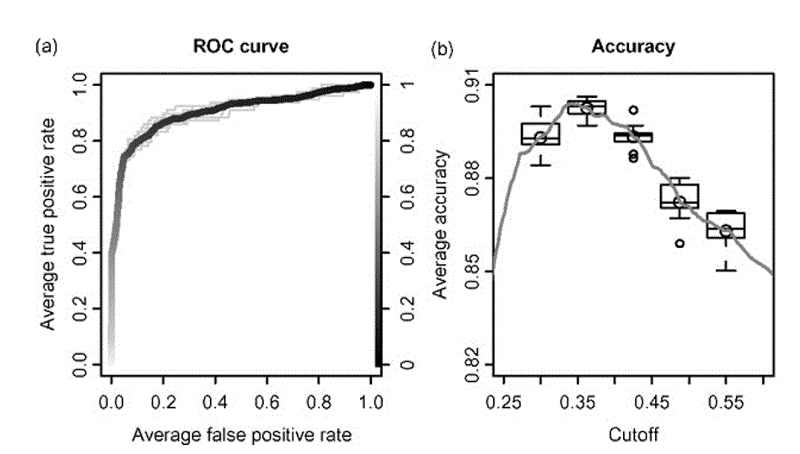
用ROCR得到的自舉法性能圖。
四、總結
上面講的有點多,但他們都圍繞著三個主題:約束建模,平滑和量化不確定性。這篇文章中所使用的圖片來自Christopher Bishop的書《模式識別和機器學習》

































