數據江湖之多元劍法 --主成分分析
招式一:主成分分析
大家好,我是媛子。相信大家從狗熊會的精品案例中啊已經體會到熊大老師的“數據江湖:回歸五式”的神通廣大了,那有的朋友就問了說,除了回歸,我還能干嘛呢?其實啊在統計里面,還有一個很好很強大的體系,叫做多元統計分析。所以呢媛子準備來跟大家系統地扒一扒,數據江湖之多元劍法。
我們這里只會講到問題的理解和結果的解讀層面,想進一步知道具體的模型設定、數學表達、方法推導、軟件實現的技術黨同學,請移步到書店找一本多元統計的教材來啃一啃,或者來修一學期媛子的多元統計課程哈。因為啊其實媛子在教課中發現,在一切交給電腦的今天呢,對于一種已經成型的方法,“怎么用”通常不是問題,用個軟件點點點或者編幾行程序就呼呼呼地跑出結果了,大家的問題一般都出在“什么時候用”和“用完了,然后呢?” 所以我們這個系列主要就集中在討論這兩件事情上面。
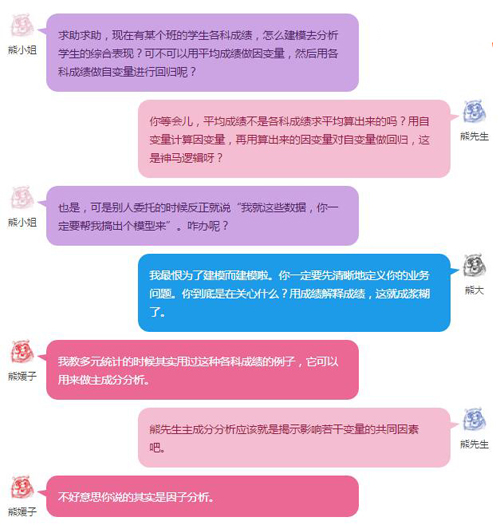
那寫下多元劍法第一招的靈感來自于下面這些我們第二期熊學院的熊孩子微信群里面的對話:
所以我們今天就不妨就著熊小姐的這個各科成績的例子,先來捋一捋“主成分分析”到底是個什么鬼。至于它跟因子分析的差別,要先搞清楚因子分析又到底是個什么鬼才能討論,所以且聽媛子下回分解這個差別的部分。
在開始之前呢,媛子還是要再強調一下熊大老師一直在強調的,做統計分析之前呢,一定一定要先清楚你的業務目的!業務目的!業務目的!重要的事情說三遍!
1
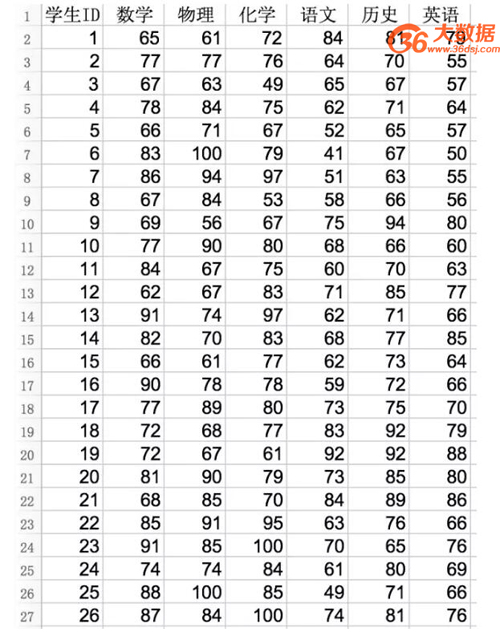
假設你現在是一名班主任,對著以下這種我們從小恨到大的成績單發呆。
那作為班主任,針對這種成績單的業務目的,就是怎么樣科學地利用以上這些各科的成績的信息來區分你班上學生的表現。當然呢你的視力和耐心足夠好的話,你可以一科一科的成績單單獨去比對,但這實在是使出洪荒之力也然并卵呀。
那通常我們怎么做呢?求平均,也就是把各科成績加起來除以科目總數,或者說求總分也是等價的。沒錯,這是一個比較合理的方法。但是媛子給你打個比方,如果有一個很奇葩的班級培養出一堆很奇葩的學生,他們的平均分都一樣,只是有的偏科嚴重,有的發展比較均衡,那這個班的學生單靠平均分就區分不開了對吧?
所以呢如果你是一名班主任,想通過成績區分一下你班上學生的表現的話,可能針對你這個班級啊,會有比平均分更好的指標,或者會有不止平均分這一個指標在等著你哦。
這個就是主成分分析(Principal Component Analysis, PCA)在做的事情:找到原始變量的線性組合,也就是所謂的主成分,使得組合后得到變量的方差最大化。被媛子繞暈了是嗎?翻譯成人話就是:找到最科學的一種或幾種綜合成績的計算方式,使得這樣計算出來的綜合得分能夠最大程度地區分這一撥學生。這里呢有幾個注意的點:
1
我們所用的計算成績組合的方法都是線性的,什么叫線性?就是說不會出現像語文成績的平方、或者數學成績的倒數這些幺蛾子。其實呢本質上我們還是在做一種各科成績的平均,但這是加權平均,并且允許有些權重可以是負數。從這些權重中我們可以看出哪些學科對于區分這一撥學生的影響比較大,并且是怎么影響的。
2
我們可能用不止一個指標去刻畫學生的表現。而這些指標呢會根據重要程度來排序,這個重要程度具體來講就是區分學生的能力。后面在結果得解讀的時候我們會進一步說明。
3
在整個過程中,我們只有一堆地位一樣的變量,沒有所謂的自變量和因變量,所以呢主成分分析不屬于回歸分析的范疇。
好了,那大家應該已經清楚主成分分析用來干嘛的了,或者說我們什么時候該用主成分分析。接下來就是噼里啪啦一頓編程實現,得到了幾個你要的綜合得分,也就是主成分(Principal Components),那么下一步就是,怎樣解讀這些指標呢?這就又回到了業務層面。我們需要做的是,結合業務知識,盡情地開腦洞。然后再看看我們的這些解讀啊跟常識現象是否相符,還有沒有什么新的發現。
這里呢我們假設最后我們通過軟件得到了如下的兩個指標,也就是主成分,也就是綜合得分的計算方式,來刻畫這個班的學生成績:
那現在問題來了,怎么理解這兩個指標呢?
指標2很好理解,基本就是我們通常見到的求平均,前面的系數呢只有輕微的不同,所以它可以用來刻畫學生各科成績的均衡表現。那么指標1呢?指標1里面呢,所有偏文科類課程成績的系數為正,偏理科的系數為負,而系數值的大小差不多。這樣算出來的是什么?基本上可以理解成是學生文科成績平均分減去理科成績平均分,也就是說,指標1刻畫的是學生文理科成績的差別,或者說是學生的偏科情況。
好,我們知道了這兩個指標大體上是什么意思,那它們能用來做什么呢?媛子總結了一下,它們可以用來做以下的三件事情:
1
它可以降低整個數據集的復雜程度,給你省事兒啊。看全班學生的六科成績多費眼費時間呀,現在只給你了兩個指標,而且我告訴你不怎么丟失重要的信息就能夠達到你的業務目的,那你這個班主任何樂而不為呀?這就是用主成分分析做降維的基本思想。那至于為什么只有兩個指標就夠了,而不是三個四個或者只有一個呢?是因為啊針對這組數據,通過計算,這兩個指標區分學生的能力(也就是說刻畫數據差異性的能力)已經占到了原來六門課能夠做到的80%了,我們就覺得足夠滿意了。當然,隔壁老王班也許需要一個或者三個指標,誰知道呢對吧。
2
我們可以用他們考量每一位學生的表現。我們傳統的成績單是給每一個學生簡單粗暴地給一個平均分或者總分。這就是上面的指標2。它的得分越高,說明該學生的均衡表現越好。那現在的成績單上又多了一項得分可正可負的指標1。如果該學生該指標的得分是個很大的正數說明什么?說明他文科比理科好得多,嚴重偏文科。反之,如果他的指標1是一個絕對值很大的負數,說明他嚴重偏理科。所以呢指標1就是學生的偏科表現,絕對值越大,偏科越嚴重。那你可能會問了,那如果指標1得分接近于0呢?那就說明他文理科成績差不多唄,可能是個全面發展的學神或者學霸,當然呢也可能是每一科都差得非常均勻的學酥或學渣。
所以通過看以上的兩個綜合指標,我們可以找出一些典型的學生,比如說指標1很高,指標2也很高,這就說明該學生是個文科學神級人物;那如果指標1很高但指標2卻很低,這就說明該學生偏科文科太嚴重,理科拖后腿,拉低平均成績啊;那如果指標1(絕對值)很低,指標2很高呢?就說明這是一個兩手抓,兩手都要硬的好寶寶對吧?以此類推。
3
我們可以用它們來刻畫班級整體的表現。我們之前提到過,這些指標是按照能夠反映這撥學生差異性的能力來排序的。那么通過這兩個指標,就可以知道這個班成績的主要特征。這里指標1排在前面,說明它比指標2,也就是簡單地求平均更能刻畫這撥學生成績的差異性。也就是說,這是一個偏科比較嚴重的班級,有的學生文科比理科好很多,有的學生反之。而且呢通過學生的指標1得分還能看出到底有多少學生文科比較好,到底有多少學生理科比較有優勢。當然辣也許換一個班,這些綜合指標的構造就完全不同了,沒準兒隔壁老王班上的學生成績的差異完全由這個數學成績主導呢。
好了,我們來總結一下今天的內容:當我們有很多個變量,又想找一種或幾種綜合指標去很好地刻畫數據的差異性的時候,主成分分析就該出馬了。那這些綜合指標怎么構造呢?是通過原來變量的加權平均,或者說線性組合來構造的。得到這些指標后,它們有什么用呢?我們可以在不丟失重要信息的前提下盡量地簡化數據集,還可以從一種全面綜合的視角來審視整個數據集,或者說我們可以去考量每一個個體的表現。
當然,不光對班主任有用,主成分分析在其他的各個領域也都有著非常直觀的應用。比如說對工業界的各個行業的各種經濟效益指標進行綜合評價啦,比如說根據人們身體的某些測量變量(像身高啊體重啊三圍啊還有各種其他的什么圍啊之類的)得出一些刻畫人身材的綜合指標,等等等等。
好的,那這次主成分分析的招式就跟大家拆到這兒。下次呢媛子會針對同樣的數據,但是從不同的業務目的出發,再跟大家來捋一捋因子分析這把刷子。感謝大家的閱讀或者收聽,我們下次見咯。